알고리즘/그래프 알고리즘
플루이드 - 워셜 알고리즘 (Floyd - Warshall algorithm)
hvv_an
2020. 8. 3. 23:57
플루이드 - 워셜 알고리즘(Floyd - Warshall algorithm)
플루이드-워셜 알고리즘은 최단 경로를 구하는 또 하나의 알고리즘이다. 알고리즘을 한 번 실행함으로써 모든 노드 간 최단 경로를 구할 수 있다.
인접 행렬을 이용하여 초기값을 설정한다.
가중치를 포함한 인접 행렬이 다음과 같다고 하자.

이 인접 행렬을 이용해서 다음과 같은 초기값을 만든다.

자신에서부터 자신까지의 거리는 항상 0이며, 직접 연결되어 있지 않은 경우에는 ∞로 초기화 한다.
초기값을 설정한 후에는 n번째 노드부터 중간 노드가 되어, 중간 노드를 거쳐 다른 노드로 갈 수 있는 값들을 업데이트시킨다. n번 반복하면 모든 노드까지의 최단 거리를 알 수 있다.
다음은 Java로 작성한 코드이다.
public class Floyd_Warshall {
public static void main(String[] args) {
int[][] adj = new int[5][5];
final int INF = 99999999;
//인접 행렬 모두 0으로 초기화
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
adj[i][j] = 0;
}
}
//인접행렬 설정
adj[0][1] = 5;
adj[0][3] = 9;
adj[0][4] = 1;
adj[1][0] = 5;
adj[1][2] = 2;
adj[2][1] = 2;
adj[2][3] = 7;
adj[3][0] = 9;
adj[3][2] = 7;
adj[3][4] = 2;
adj[4][0] = 1;
adj[4][3] = 2;
//거리 행렬 설정
int[][] dist = new int[5][5];
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
if(i==j) {
dist[i][j] = 0;
}else if(adj[i][j] != 0) {
dist[i][j] = adj[i][j];
}else {
dist[i][j] = INF;
}
}
}
//최단 거리 구하기
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
for (int k = 0; k < 5; k++) {
dist[i][j] = Math.min(dist[i][j], dist[i][k]+dist[k][j]);
}
}
}
//출력
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
System.out.print(dist[i][j]+" ");
}
System.out.println();
}
}
}
k번째 노드가 중간 노드가 되어 시작 노드부터 중간 노드 + 중간 노드부터 도착 노드까지의 거리가 현재 저장된 시작~도착까지의 거리보다 작으면 업데이트해주면 된다.
for loop를 3중으로 실행해야 한다. 즉, 시간 복잡도는 O(n^3)를 갖는다.
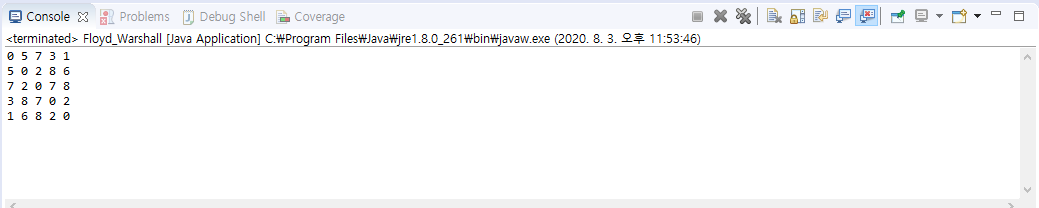
다음은 출력 값이다.