문제 설명
| 2 초 | 256 MB | 6632 | 1997 | 1368 | 30.427% |
문제
크기가 M×M인 격자 형태의 벌집이 있다. 이 벌집의 각 칸에는 여왕벌이 될 애벌레들이 한 마리씩 자라고 있다.
격자칸의 좌표계를 다음과 같이 설정한다. 제일 왼쪽 위 칸의 좌표는 (0,0)이다. 그 아래쪽 칸들의 좌표는 순서대로 (1,0), (2,0), ...등이다. 좌표가 (i,0)인 칸의 오른쪽 칸들의 좌표는 순서대로 (i, 1), (i,2), ... 등이다.
애벌레들은 매일 에너지를 모아서 정오(낮 12시) 에 한번 자라는데, 여기에 걸리는 시간은 매우 짧아서 무시할 수 있다. 첫날 아침 모든 애벌레들의 크기는 1이고, 이러한 과정을 N일 동안 반복한다.
각 애벌레가 자라서 크기가 커지는 정도는 하루에 +0, +1, +2의 세 가지 중 하나이다. 더하기(+) 기호는 앞으로 생략한다. 구체적으로 각 애벌레가 자라는 정도를 결정하는 규칙은 다음과 같다.
- 제일 왼쪽 열과, 제일 위쪽 행의 애벌레들은 자신이 자라는 정도를 스스로 결정한다. 이들은 입력으로 주어질 것이다. 애벌레들이 자라는 정도를 왼쪽 제일 아래 칸에서 시작하여 위쪽으로 가면서 읽고, 제일 위쪽 칸에 도착하면 오른쪽으로 가면서 행의 끝까지 읽었다고 하자. 모든 입력에서 이렇게 읽은 값들은 감소하지 않는 형태이다.
- 나머지 애벌레들은 자신의 왼쪽(L), 왼쪽 위(D), 위쪽(U)의 애벌레들이 다 자란 다음, 그 날 가장 많이 자란 애벌레가 자란 만큼 자신도 자란다.
M = 4, N = 2인 예를 하나 들어보자. 다음은 각 격자에 있는 애벌레의 첫날 아침의 크기이다.
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
2일 동안 제일 왼쪽 열과 제일 위쪽 행에 있는 7마리의 애벌레들이 자라는 정도를 왼쪽 제일 아래칸에서 시작하여 위쪽으로 가면서 읽고, 제일 위쪽 칸에 도착하면 오른쪽으로 가면서 행의 끝까지 읽었을 때, 다음과 같다고 하자.
- 1일: 0, 0, 1, 1, 1, 2, 2
- 2일: 1, 1, 1, 1, 1, 1, 2
첫날 저녁에 애벌레들은 아래와 같은 크기를 가진다. 예를 들어, 좌표 (1,1)의 애벌레는 왼쪽 애벌레의 크기가 1만큼 자랐고, 왼쪽 위의 애벌레가 1만큼 자랐고, 위쪽 애벌레도 1만큼 자랐으므로, 자신도 1만큼을 자란다. 또, 좌표 (3,3)의 애벌레는 규칙을 따르면 2만큼 자람을 알 수 있다.
| 2 | 2 | 3 | 3 |
| 2 | 2 | 3 | 3 |
| 1 | 2 | 3 | 3 |
| 1 | 2 | 3 | 3 |
둘째 날이 지났을 때는 동일한 과정에 따라 다음과 같이 됨을 확인할 수 있다.
| 3 | 3 | 4 | 5 |
| 3 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 |
격자칸의 크기, 날자 수, 날자별 제일 왼쪽 열과 제일 위쪽 행의 애벌레들이 자라는 정도를 입력으로 받아 마지막 날 저녁의 애벌레들의 크기를 출력하는 프로그램을 작성하라
제한 사항


풀이
문제를 요약하면, 애벌레가 하루씩 성장하는데, 왼쪽과 위쪽 테두리 애벌레는 성장치가 정해져 있다.
이외의 애벌레는 왼쪽, 왼쪽 윗 대각, 위쪽 3칸 중 가장 큰 성장치를 따라 성장한다.
예를 들어 보자.
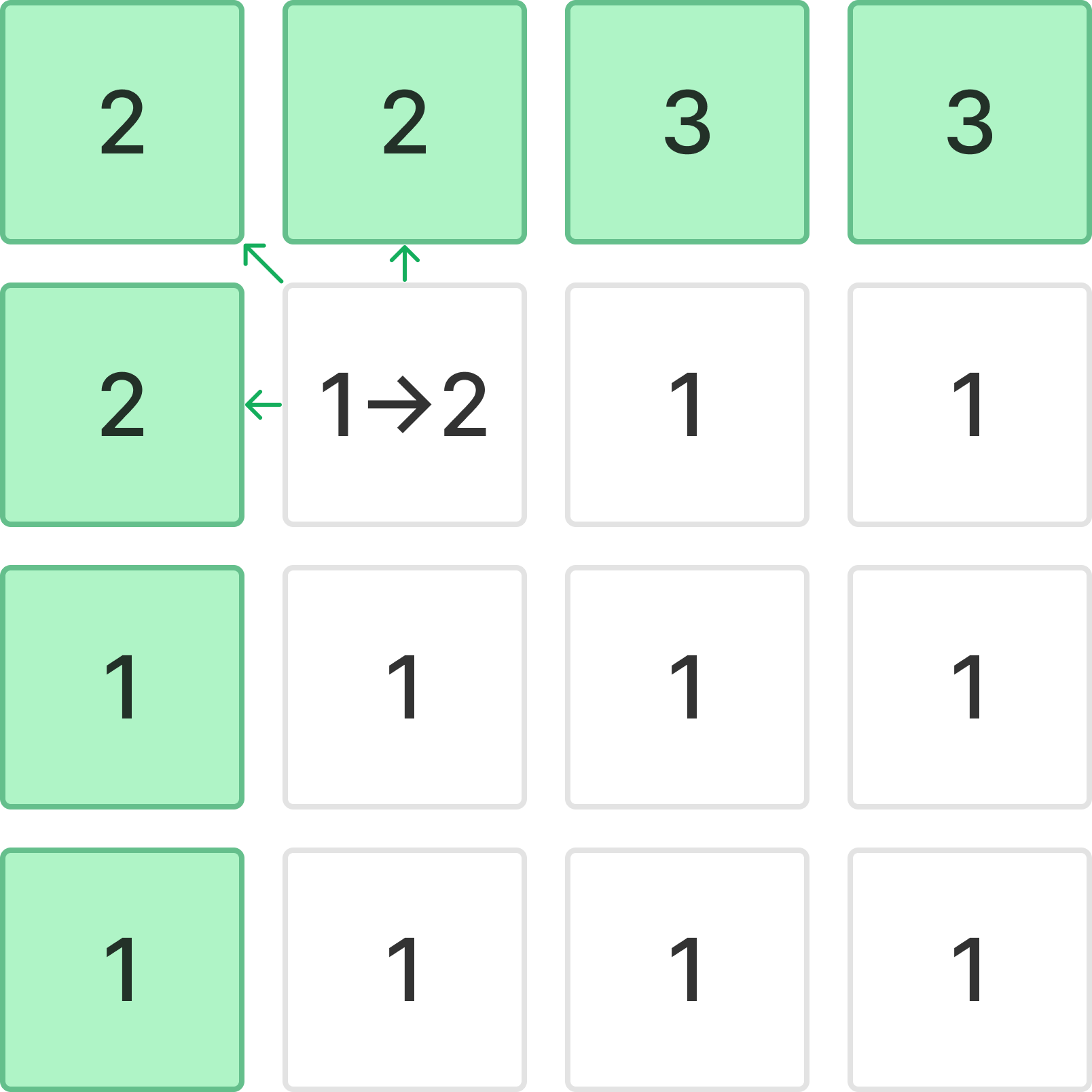
(1,1)의 애벌레는 (0,0), (1,0), (0,1) 중 가장 큰 성장치에 따라 성장한다.
예시에서는 모두 1씩 성장했기 때문에 똑같이 2로 성장한다.
이 문제를 풀기 위해서는 2가지 주의할 점이 있다.
- 애벌레의 성장치는 증가하는 수열이다.
- 성장치가 왼쪽 아래에서 오른쪽 위로 진행된다.
우선, 문제를 간단하게 풀면 $O(N*M *M)$에 문제를 풀 수 있다.
하나하나 더하면 된다.
이렇게 하면 시간초과가 발생한다. N이 매우 크기 때문이다.
그렇다면 최적화가 필요하다.
최적화의 비밀은 애벌레의 성장치가 증가하는 수열이라는 것이다.
애벌레는 주변에 있는 애벌레의 성장치에 따라 성장하는데, 주변은 자신의 위쪽이 끝이다.
즉, 성장치가 항상 증가하기 때문에 자신의 위칸이 가장 많이 성장하는 애벌레이다.
따라서, 자신이 속한 열의 가장 윗 행이 성장한 만큼 아래 애벌레들은 성장한다.
정리하자면 풀이법은 다음과 같다.
- 입력을 받을 때, 테두리에 대해 모두 더해 미리 계산한다.
- (1,1)부터 (M-1, M-1)까지 가장 윗행의 성장치만큼 더한다.
예를 들어 보자.
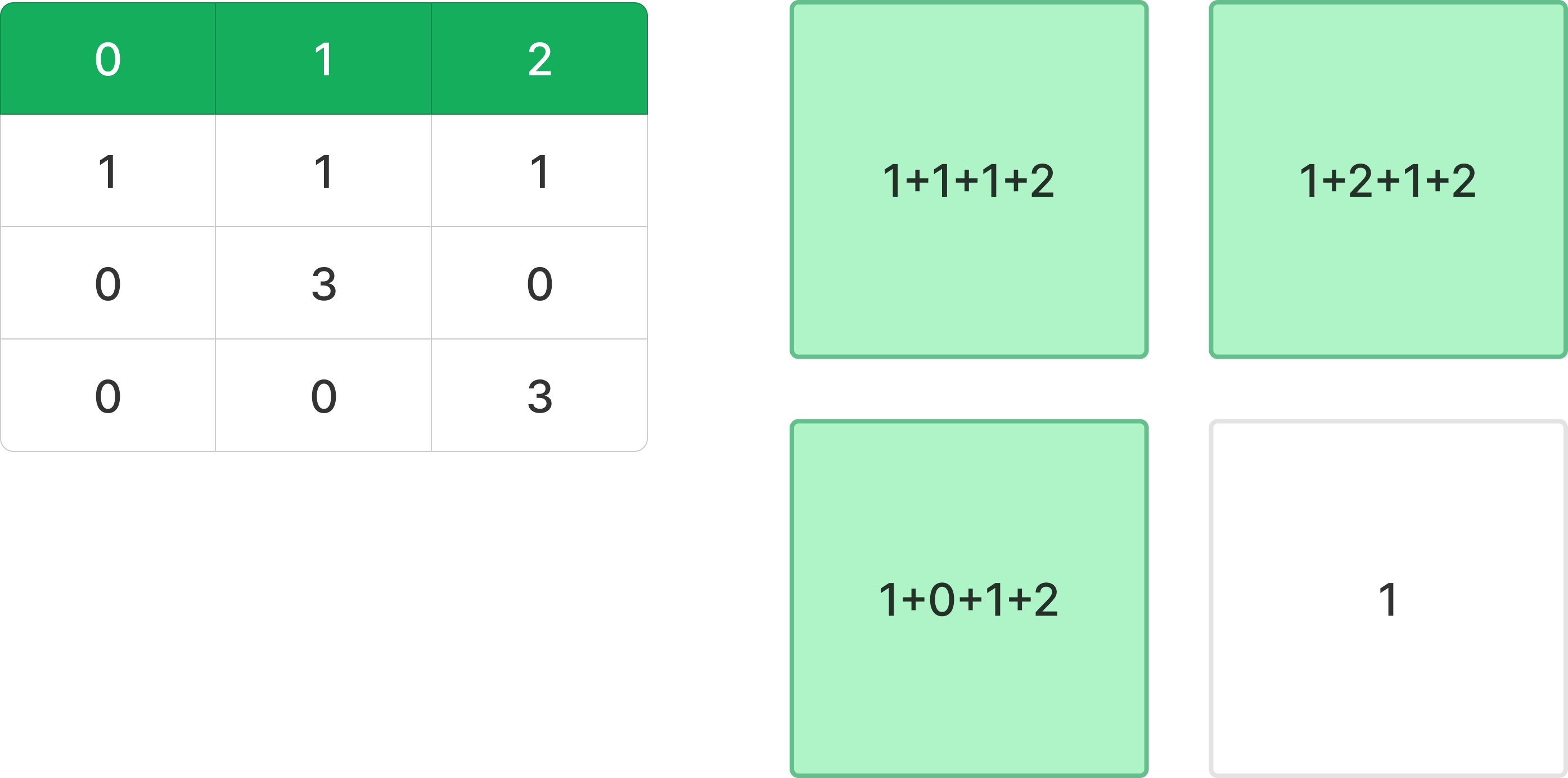
입력을 받는 과정에서 테두리의 성장치를 미리 계산할 수 있다.
for (int i = 0; i < N; i++)
{
int idx = 0;
for (int j = 0; j < 3; j++)
{
int num;
cin >> num;
for (int k = 0; k < num; k++) growth[idx++] += j;
}
}이후, 색이 칠해지지 않은 칸은 자신의 윗 칸이 가장 많이 성장한 애벌레이다.
따라서, 해당 칸의 성장치를 밑으로 전파하여 더해주면 된다.
int idx = 0;
for (int j = M - 1; j >= 0; j--) larvas[j][0] += growth[idx++];
for (int x = 1; x < M; x++)
{
for (int y = 0; y < M; y++)
{
larvas[y][x] += growth[idx];
}
idx++;
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int M, N;
void Print(vector<vector<int>>& larvas)
{
for (auto row : larvas)
{
for (auto larva : row)
{
cout << larva << " ";
}
cout << "\n";
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> M >> N;
const int GROWSIZE = M * 2 - 1;
vector<int> growth(GROWSIZE,0);
vector<vector<int>> larvas(M, vector<int>(M, 1));
for (int i = 0; i < N; i++)
{
int idx = 0;
for (int j = 0; j < 3; j++)
{
int num;
cin >> num;
for (int k = 0; k < num; k++) growth[idx++] += j;
}
}
int idx = 0;
for (int j = M - 1; j >= 0; j--) larvas[j][0] += growth[idx++];
for (int x = 1; x < M; x++)
{
for (int y = 0; y < M; y++)
{
larvas[y][x] += growth[idx];
}
idx++;
}
Print(larvas);
return 0;
}