문제 설명
N×N의 표에 수 N2개 채워져 있다. 채워진 수에는 한 가지 특징이 있는데, 모든 수는 자신의 한 칸 위에 있는 수보다 크다는 것이다. N=5일 때의 예를 보자.
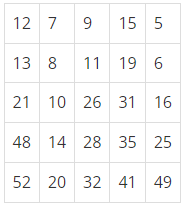
이러한 표가 주어졌을 때, N번째 큰 수를 찾는 프로그램을 작성하시오. 표에 채워진 수는 모두 다르다.
제한 사항


풀이
문제를 요약하면, N*N 배열에서 N번째 큰 수를 찾아내는 것이다.
이때, 배열의 수는 자신의 위칸보다는 큰 수가 저장된다는 규칙이 있다.
해당 문제의 풀이는 다양하다.
우선, 간단한 풀이는 N*N개의 수를 입력받아 정렬한 뒤 N번째 큰 수를 찾는 것이다.
vector<int> Nums(N*N, 0);
for (int i = 0; i < N * N; i++)
{
cin >> Nums[i];
}
sort(Nums.begin(), Nums.end(), greater());
cout << Nums[N - 1];
나머지 풀이는 문제의 규칙을 이용하는 것이다.
배열의 수들은 자신의 윗칸보다 무조건 크다.
따라서, 가장 큰 수는 가장 아랫줄에 있을 것이다.
그렇다면, 두 번째로 큰 수는 가장 아랫줄 + 가장 큰 수의 위칸에 존재한다.
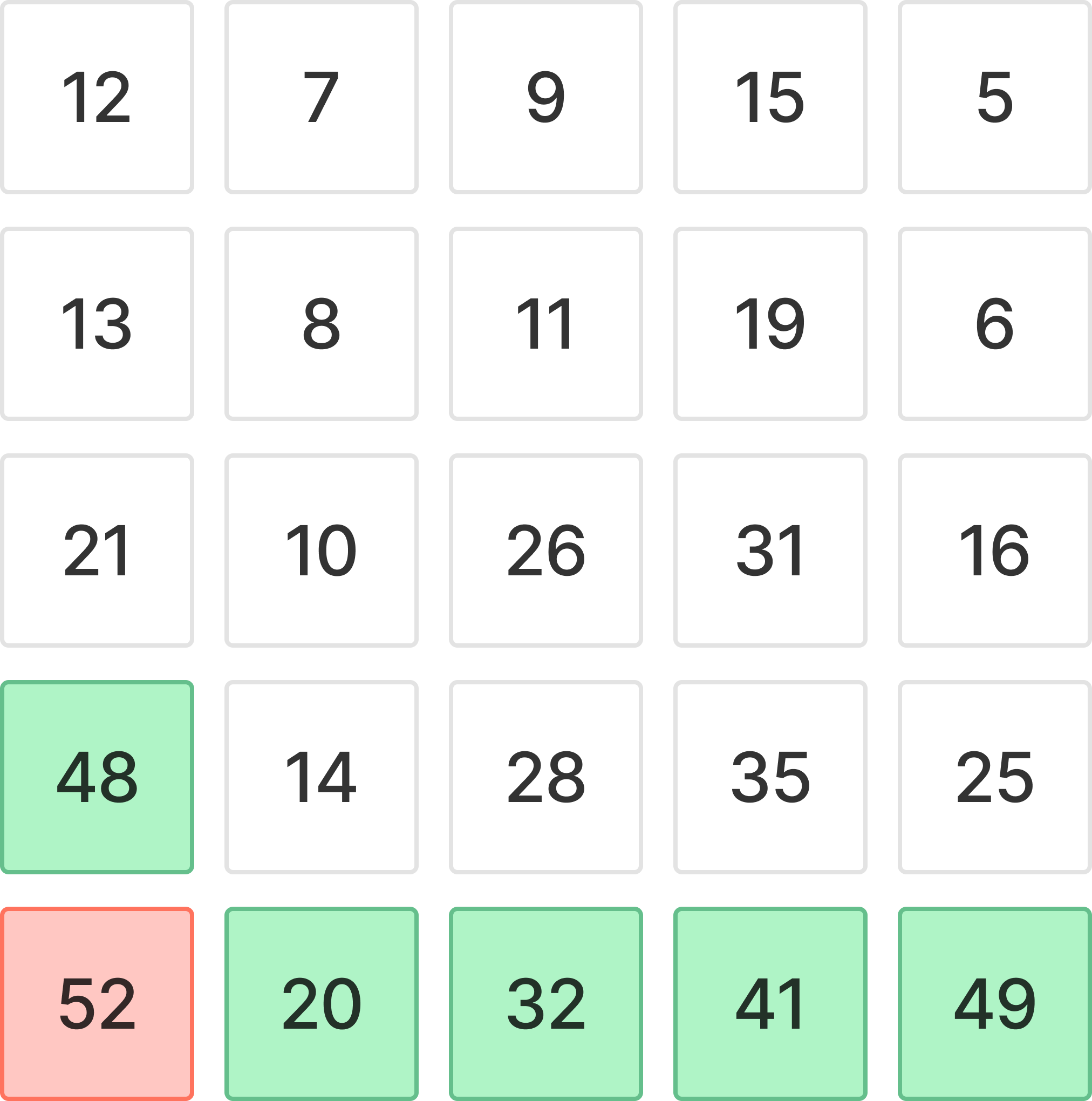
52가 가장 큰 수이고, 그다음으로 큰 수는 초록색중 하나가 된다는 뜻이다.
즉, 우선순위 큐를 통해 가장 큰 수를 찾아내고 우선순위 큐에 그 위칸의 수를 넣은 뒤 N-1번 반복하면 우선순위 큐의 top에 N번째 큰 수가 있게 된다.
priority_queue < tuple<int, int, int>, vector<tuple<int, int, int>>> pq;
for (int i = 0; i < N; i++)
{
pq.push({ Nums[N - 1][i], N - 1, i });
}
for (int i = 0; i < N-1; i++)
{
auto [num, y, x] = pq.top();
pq.pop();
if (y == 0) continue;
pq.push({ Nums[y - 1][x], y - 1, x });
}정렬로 문제를 푸는 것에 비해 메모리는 조금 손해를 보지만, 시간을 단축시킬 수 있다.

전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <bitset>
using namespace std;
int N;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<int>> Nums(N, vector<int>(N, 0));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> Nums[i][j];
}
}
priority_queue < tuple<int, int, int>, vector<tuple<int, int, int>>> pq;
for (int i = 0; i < N; i++)
{
pq.push({ Nums[N - 1][i], N - 1, i });
}
for (int i = 0; i < N-1; i++)
{
auto [num, y, x] = pq.top();
pq.pop();
if (y == 0) continue;
pq.push({ Nums[y - 1][x], y - 1, x });
}
auto [ans, y, x] = pq.top();
cout << ans;
return 0;
}
