문제 설명
출판사의 편집자인 어피치는 네오에게 컬러링북에 들어갈 원화를 그려달라고 부탁하여 여러 장의 그림을 받았다. 여러 장의 그림을 난이도 순으로 컬러링북에 넣고 싶었던 어피치는 영역이 많으면 색칠하기가 까다로워 어려워진다는 사실을 발견하고 그림의 난이도를 영역의 수로 정의하였다. (영역이란 상하좌우로 연결된 같은 색상의 공간을 의미한다.)
그림에 몇 개의 영역이 있는지와 가장 큰 영역의 넓이는 얼마인지 계산하는 프로그램을 작성해보자.
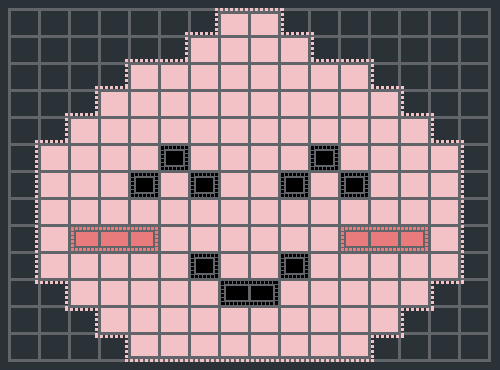
위의 그림은 총 12개 영역으로 이루어져 있으며, 가장 넓은 영역은 어피치의 얼굴면으로 넓이는 120이다.
https://school.programmers.co.kr/learn/courses/30/lessons/1829
입력 형식
입력은 그림의 크기를 나타내는 m과 n, 그리고 그림을 나타내는 m × n 크기의 2차원 배열 picture로 주어진다. 제한조건은 아래와 같다.
- 1 <= m, n <= 100
- picture의 원소는 0 이상 2^31 - 1 이하의 임의의 값이다.
- picture의 원소 중 값이 0인 경우는 색칠하지 않는 영역을 뜻한다.
풀이
bfs를 이용하여 간단하게 문제를 풀 수 있다.
picture의 모든 요소를 확인하며 bfs를 진행하면서 같은 값을 갖는 개수를 세면 된다.
이때, 이미 방문한 요소를 중복으로 세지 않게 하기 위해 방문 여부를 체크한다.
또한, 전역변수를 사용하려면 초기화를 먼저 해주어야 한다.
이거 때문에 5분 더 걸렸다.
전체 코드
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
int bfs(int startY, int startX, vector<vector<int>>& picture, vector<vector<bool>>& visited, vector<pair<int,int>>& dir)
{
int m = picture.size();
int n = picture[0].size();
int val = picture[startY][startX];
int cnt = 1;
queue<pair<int,int>> q;
q.push({startY, startX});
visited[startY][startX] = true;
while(!q.empty())
{
int y = q.front().first;
int x = q.front().second;
q.pop();
for(int i = 0 ; i < 4; i++)
{
int new_y = y + dir[i].first;
int new_x = x + dir[i].second;
if(new_y < 0 || new_y >= m || new_x < 0 || new_x >= n) continue;
if(visited[new_y][new_x]) continue;
if(picture[new_y][new_x] != val) continue;
visited[new_y][new_x] = true;
q.push({new_y, new_x});
cnt++;
}
}
return cnt;
}
vector<int> solution(int m, int n, vector<vector<int>> picture) {
int number_of_area = 0;
int max_size_of_one_area = 0;
vector<vector<bool>> visited(m, vector<bool>(n, false));
vector<pair<int,int>> dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
for(int i = 0; i < m; i++)
{
for(int j = 0 ; j < n; j++)
{
if(visited[i][j]) continue;
if(picture[i][j] == 0) continue;
max_size_of_one_area = max(bfs(i, j, picture, visited, dir), max_size_of_one_area);
number_of_area++;
}
}
vector<int> answer(2);
answer[0] = number_of_area;
answer[1] = max_size_of_one_area;
return answer;
}
