문제 설명
재현이는 주변을 살펴보던 중 체스판과 말을 이용해서 새로운 게임을 만들기로 했다. 새로운 게임은 크기가 N×N인 체스판에서 진행되고, 사용하는 말의 개수는 K개이다. 말은 원판모양이고, 하나의 말 위에 다른 말을 올릴 수 있다. 체스판의 각 칸은 흰색, 빨간색, 파란색 중 하나로 색칠되어있다.
게임은 체스판 위에 말 K개를 놓고 시작한다. 말은 1번부터 K번까지 번호가 매겨져 있고, 이동 방향도 미리 정해져 있다. 이동 방향은 위, 아래, 왼쪽, 오른쪽 4가지 중 하나이다.
턴 한 번은 1번 말부터 K번 말까지 순서대로 이동시키는 것이다. 한 말이 이동할 때 위에 올려져 있는 말도 함께 이동하며, 가장 아래에 있는 말만 이동할 수 있다. 말의 이동 방향에 있는 칸에 따라서 말의 이동이 다르며 아래와 같다. 턴이 진행되던 중에 말이 4개 이상 쌓이는 순간 게임이 종료된다.
- A번 말이 이동하려는 칸이
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
- A번 말의 위에 다른 말이 있는 경우에는 A번 말과 위에 있는 모든 말이 이동한다.
- 예를 들어, A, B, C로 쌓여있고, 이동하려는 칸에 D, E가 있는 경우에는 A번 말이 이동한 후에는 D, E, A, B, C가 된다.
- 빨간색인 경우에는 이동한 후에 A번 말과 그 위에 있는 모든 말의 쌓여있는 순서를 반대로 바꾼다.
- A, B, C가 이동하고, 이동하려는 칸에 말이 없는 경우에는 C, B, A가 된다.
- A, D, F, G가 이동하고, 이동하려는 칸에 말이 E, C, B로 있는 경우에는 E, C, B, G, F, D, A가 된다.
- 파란색인 경우에는 A번 말의 이동 방향을 반대로 하고 한 칸 이동한다. 방향을 반대로 한 후에 이동하려는 칸이 파란색인 경우에는 이동하지 않고 방향만 반대로 바꾼다.
- 체스판을 벗어나는 경우에는 파란색과 같은 경우이다.
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
다음은 크기가 4×4인 체스판 위에 말이 4개 있는 경우이다.
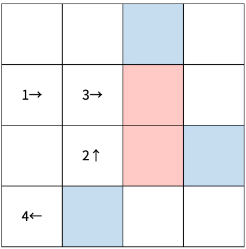
첫 번째 턴은 다음과 같이 진행된다.
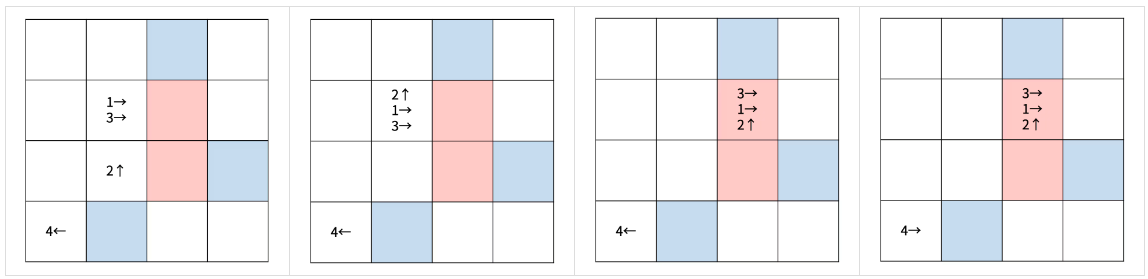
두 번째 턴은 다음과 같이 진행된다.
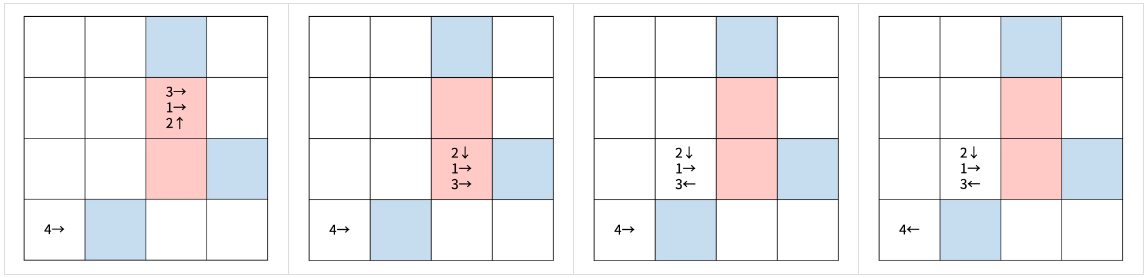
체스판의 크기와 말의 위치, 이동 방향이 모두 주어졌을 때, 게임이 종료되는 턴의 번호를 구해보자.
제한 사항
첫째 줄에 체스판의 크기 N, 말의 개수 K가 주어진다. 둘째 줄부터 N개의 줄에 체스판의 정보가 주어진다. 체스판의 정보는 정수로 이루어져 있고, 각 정수는 칸의 색을 의미한다. 0은 흰색, 1은 빨간색, 2는 파란색이다.
다음 K개의 줄에 말의 정보가 1번 말부터 순서대로 주어진다. 말의 정보는 세 개의 정수로 이루어져 있고, 순서대로 행, 열의 번호, 이동 방향이다. 행과 열의 번호는 1부터 시작하고, 이동 방향은 4보다 작거나 같은 자연수이고 1부터 순서대로 →, ←, ↑, ↓의 의미를 갖는다.
같은 칸에 말이 두 개 이상 있는 경우는 입력으로 주어지지 않는다.
게임이 종료되는 턴의 번호를 출력한다. 그 값이 1,000보다 크거나 절대로 게임이 종료되지 않는 경우에는 -1을 출력한다.
- 4 ≤ N ≤ 12
- 4 ≤ K ≤ 10
풀이
문제를 요약하면, K개의 체스말을 규칙에 맞게 순서대로 움직인 후, 4개 이상의 체스말이 겹치기까지 몇 턴이 걸리는지 구하는 것이다.
보드에는 흰색, 빨간색, 파란색의 칸이 있고 각 칸은 고유의 규칙이 있다.
- 흰색: 순서대로 이동
- 빨간색: 쌓여있는 순서를 반대로 바꿈
- 파란색: 제일 아래에 있는 말의 이동방향을 반대로 바꿈
또한, 보드 밖으로 넘어가는 것도 파란색과 동일하게 처리한다.
그리고 가장아래 있는 말이 아니면 이동할 수 없다.
이런 규칙에 맞춰 이동하면 되는데, 꽤 귀찮고 복잡한 작업이다.
즉, 이 문제는 특별한 알고리즘은 없고 규칙을 구현하는 문제이다.
몇 가지 규칙을 간단하게 만드는 트릭이 있다.
우선, 행위 단위로 함수를 분리한다.
- 종료 조건 판단
- 체스말 이동
종료 조건 판단은 모든 칸을 순회하며 4개 이상 겹쳐진 칸이 있는지 확인하면 된다.
체스말을 이동할 때는 이동할 칸의 색에 따라 구현한다.
흰색 칸은 배열의 앞에서부터 다음 칸으로 옮긴 뒤 현재 칸을 모두 제거한다.
빨간색 칸은 순서가 바뀌어야 하기 때문에 현재 칸이 빌 때까지 뒤에서부터 제거하여 이동할 칸에 채워 넣으면 된다.
파란색 칸은 제일 아래 칸의 이동 방향을 바꾸면 되는데, 방향을 짝이 되는 방향끼리 묶어 계산할 수 있게 이동 방향을 바꾸었다.
예를 들어, 오른쪽이 0이었다면, 왼쪽이 2, 위쪽이 1이라면 아래쪽을 3으로 설정하여 해당 방향에 2를 더해 4로 나눈 나머지가 반대방향이 된다.
dir = (dir + 2) % 4;이를 통해 간단하게 방향을 바꿀 수 있다.
또한, 자료구조를 잘 써야 한다.
칸의 색깔을 저장하는 이차원 배열, 체스말을 저장할 배열 등이 필요하다.
만약, 체스말에 대한 정보를 이차원 배열에 넣어 관리한다면 어떤 말을 이동할지 찾아야 하며 이미 이동한 말과 그렇지 않은 말을 분리해야 하는 번거로움이 있다.
따라서, 체스말 자체를 저장하는 배열을 따로 관리해 순서대로 이동하기 간편하게 만들었다.
vector<vector<int>> Color(N, vector<int>(N, 0)); // 칸의 색깔
vector<vector<vector<int>>> Board(N, vector<vector<int>>(N)); // 현재 체스판
vector<tuple<int,int,int>> Pawn(K); // 체스말
이제 순서대로 말을 이동하며 완료여부를 체크하면 된다.
int cnt = 0;
while (!CheckEnd(Board) && cnt <= 1000)
{
for (int i = 0; i < K; i++)
{
int y = get<0>(Pawn[i]);
int x = get<1>(Pawn[i]);
int& d = get<2>(Pawn[i]);
//제일 아래X => 못움직임
if (Board[y][x][0] != i) continue;
Move(Board, Color, Pawn, y, x, d);
}
cnt++;
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
using namespace std;
enum DIR
{
RIGHT,
UP,
LEFT,
DOWN
};
enum BLANKCOLOR
{
WHITE,
RED,
BLUE
};
vector<int> dy = { 0, -1, 0, 1 };
vector<int> dx = { 1, 0, -1, 0 };
bool CheckEnd(vector<vector<vector<int>>>& Board)
{
for (auto row : Board)
{
for (auto cell : row)
{
if (cell.size() >= 4) return true;
}
}
return false;
}
void Move(vector<vector<vector<int>>>& Board, vector<vector<int>>& Color, vector<tuple<int, int, int>>& Pawn, int y, int x, int& dir)
{
int newY = y + dy[dir];
int newX = x + dx[dir];
if (newY < 0 || newY >= Board.size() || newX < 0 || newX >= Board.size())
{
//반대로
dir = (dir + 2) % 4;
newY = y + dy[dir];
newX = x + dx[dir];
if (Color[newY][newX] == BLUE) return;
Move(Board, Color, Pawn, y, x, dir);
return;
}
switch (Color[newY][newX])
{
case WHITE:
for (auto pawn : Board[y][x])
{
Board[newY][newX].push_back(pawn);
get<0>(Pawn[pawn]) = newY;
get<1>(Pawn[pawn]) = newX;
}
while (!Board[y][x].empty()) Board[y][x].pop_back();
break;
case RED:
while (!Board[y][x].empty())
{
auto temp = Board[y][x].back();
Board[newY][newX].push_back(temp);
Board[y][x].pop_back();
get<0>(Pawn[temp]) = newY;
get<1>(Pawn[temp]) = newX;
}
break;
case BLUE:
dir = (dir + 2) % 4;
newY = y + dy[dir];
newX = x + dx[dir];
if ((newY < 0 || newY >= Board.size() || newX < 0 || newX >= Board.size())) break;
if (Color[newY][newX] == BLUE) break;
Move(Board, Color, Pawn, y, x, dir);
break;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int N, K;
cin >> N >> K;
vector<vector<int>> Color(N, vector<int>(N, 0));
vector<vector<vector<int>>> Board(N, vector<vector<int>>(N));
vector<tuple<int,int,int>> Pawn(K);
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> Color[i][j];
}
}
for (int i = 0; i < K; i++)
{
int r, c, d, dir;
cin >> r >> c >> d;
if (d == 1) dir = RIGHT;
else if (d == 2) dir = LEFT;
else if (d == 3) dir = UP;
else dir = DOWN;
Pawn[i] = { r - 1, c - 1, dir };
Board[r-1][c-1].push_back(i);
}
int cnt = 0;
while (!CheckEnd(Board) && cnt <= 1000)
{
for (int i = 0; i < K; i++)
{
int y = get<0>(Pawn[i]);
int x = get<1>(Pawn[i]);
int& d = get<2>(Pawn[i]);
//제일 아래X => 못움직임
if (Board[y][x][0] != i) continue;
Move(Board, Color, Pawn, y, x, d);
}
cnt++;
}
if (cnt <= 1000) cout << cnt;
else cout << -1;
return 0;
}