문제 설명
두 마리의 백조가 호수에서 살고 있었다. 그렇지만 두 마리는 호수를 덮고 있는 빙판으로 만나지 못한다.
호수는 행이 R개, 열이 C개인 직사각형 모양이다. 어떤 칸은 얼음으로 덮여있다.
호수는 차례로 녹는데, 매일 물 공간과 접촉한 모든 빙판 공간은 녹는다. 두 개의 공간이 접촉하려면 가로나 세로로 닿아 있는 것만 (대각선은 고려하지 않는다) 생각한다.
아래에는 세 가지 예가 있다.
...XXXXXX..XX.XXX ....XXXX.......XX .....XX..........
....XXXXXXXXX.XXX .....XXXX..X..... ......X..........
...XXXXXXXXXXXX.. ....XXX..XXXX.... .....X.....X.....
..XXXXX..XXXXXX.. ...XXX....XXXX... ....X......XX....
.XXXXXX..XXXXXX.. ..XXXX....XXXX... ...XX......XX....
XXXXXXX...XXXX... ..XXXX.....XX.... ....X............
..XXXXX...XXX.... ....XX.....X..... .................
....XXXXX.XXX.... .....XX....X..... .................
처음 첫째 날 둘째 날백조는 오직 물 공간에서 세로나 가로로만(대각선은 제외한다) 움직일 수 있다.
며칠이 지나야 백조들이 만날 수 있는 지 계산하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/3197
3197번: 백조의 호수
입력의 첫째 줄에는 R과 C가 주어진다. 단, 1 ≤ R, C ≤ 1500. 다음 R개의 줄에는 각각 길이 C의 문자열이 하나씩 주어진다. '.'은 물 공간, 'X'는 빙판 공간, 'L'은 백조가 있는 공간으로 나타낸다.
www.acmicpc.net
제한 사항
입력의 첫째 줄에는 R과 C가 주어진다. 단, 1 ≤ R, C ≤ 1500.
다음 R개의 줄에는 각각 길이 C의 문자열이 하나씩 주어진다. '.'은 물 공간, 'X'는 빙판 공간, 'L'은 백조가 있는 공간으로 나타낸다.
풀이
문제를 요약하면, 물은 ".", 빙하는 "X"로 표현한다.
물 옆에 있는 빙하는 하루가 지나면 녹는다.
백조는 빙하가 있는 칸은 지나갈 수 없다.
이러한 상황에서 두 백조가 며칠만에 만날 수 있는지 구해야 한다.
문제를 보고 BFS를 통해 해결할 수 있다고 생각했다.
하지만, 이 문제가 플레티넘인 이유는 메모리에 있었다.
일반적인 BFS를 돌리면 메모리 초과가 발생한다.
방문 여부를 체크해도 똑같다.
메모리 초과를 해결하기 위해서는 트릭이 필요하다.
우선, 입력을 받는 과정에서 물과 빙하, 백조의 위치까지 분리할 수 있다.
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
cin >> lake[i][j];
if (lake[i][j] == '.' || lake[i][j] == 'L') water.push({i, j});
if (lake[i][j] == 'L' && canMove.empty()) canMove.push({ i, j });
}
}백조는 하나만 있어도 다른 백조에 도달할 수 있기 때문에 하나만 관리한다.
둘째로, 빙하가 녹아내리는 과정을 트래킹하며 테두리만 큐에 담아 관리해야 한다.
입력과정에서 모든 물(.)을 큐에 담아두었다.
어떤 부분이 빙하와 인접해있는지 모르기 때문이다.
따라서, 처음에는 모든 물을 검사하여 사방에 빙하가 있다면 그 빙하는 녹아내리고 녹은 빙하가 물의 테두리가 된다.
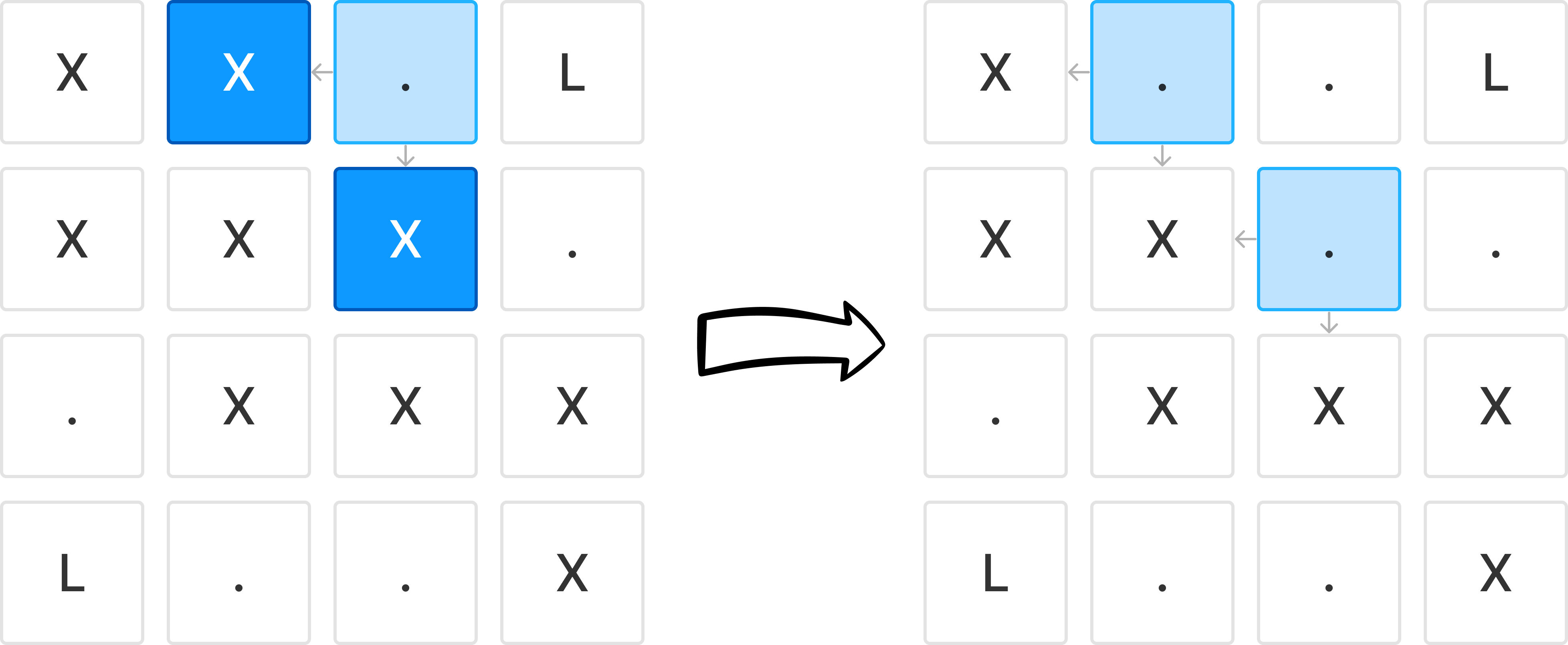
물과 인접한 빙하는 이번에 녹아내리고 녹아내린 빙하가 물의 테두리가 되어 다음날에 인접한 빙하를 녹인다.
즉, 모든 물을 큐에 담아둘 필요없이 테두리만 큐로 관리하면 된다.
void Melt(vector<vector<char>>& lake, queue<pair<int, int>>& water)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
int waterCnt = water.size();
while (waterCnt--)
{
auto [y, x] = water.front();
water.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (lake[newY][newX] == 'X')
{
lake[newY][newX] = '.';
water.push({ newY, newX });
}
}
}
}
셋째로, 두 백조가 만나는지에 대해 체크하는 부분 역시 BFS로 구할 수 있지만 메모리 초과 때문에 위와 같은 트릭을 써야 한다.
이번에는 백조가 움직일 수 있는 부분의 끝만 트래킹하면 된다.
즉, 백조가 움직이다가 빙하를 만나는 지점은 다음날에 녹아내리며 백조가 움직일 수 있는 끝부분이 된다.
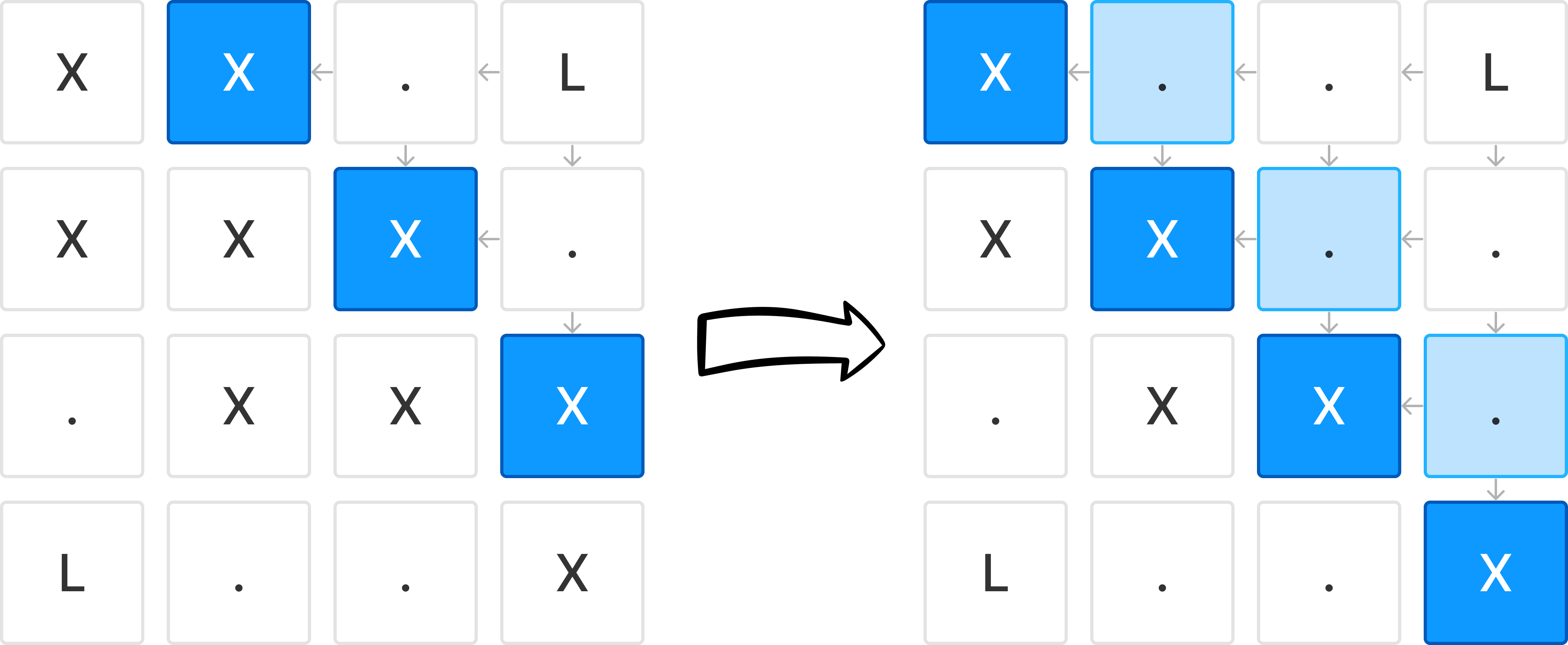
다음날부터는 백조가 움직일 수 있는 끝부분에서 BFS를 시작하면 된다.
이미 지나온 길은 다시 확인할 필요없기 때문이다.
bool Check(vector<vector<char>>& lake, queue<pair<int,int>>& canMove, vector<vector<bool>>& visited)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
queue<pair<int, int>> nextCanMove;
while (!canMove.empty())
{
auto [y, x] = canMove.front();
canMove.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
if (lake[newY][newX] == 'X')
{
nextCanMove.push({ newY, newX });
continue;
}
if (lake[newY][newX] == 'L') return true;
canMove.push({ newY, newX });
}
}
canMove = move(nextCanMove);
return false;
}
전체 코드
#include <stdio.h>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;
bool Check(vector<vector<char>>& lake, queue<pair<int,int>>& canMove, vector<vector<bool>>& visited)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
queue<pair<int, int>> nextCanMove;
while (!canMove.empty())
{
auto [y, x] = canMove.front();
canMove.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
if (lake[newY][newX] == 'X')
{
nextCanMove.push({ newY, newX });
continue;
}
if (lake[newY][newX] == 'L') return true;
canMove.push({ newY, newX });
}
}
canMove = move(nextCanMove);
return false;
}
void Melt(vector<vector<char>>& lake, queue<pair<int, int>>& water)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
int waterCnt = water.size();
while (waterCnt--)
{
auto [y, x] = water.front();
water.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (lake[newY][newX] == 'X')
{
lake[newY][newX] = '.';
water.push({ newY, newX });
}
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int R, C;
cin >> R >> C;
vector<vector<char>> lake(R, vector<char>(C, 0));
vector<vector<bool>> visited(R, vector<bool>(C, false));
queue<pair<int, int>> canMove;
queue<pair<int, int>> water;
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
cin >> lake[i][j];
if (lake[i][j] == '.' || lake[i][j] == 'L') water.push({i, j});
if (lake[i][j] == 'L' && canMove.empty()) canMove.push({ i, j });
}
}
auto [swanY, swanX] = canMove.front();
visited[swanY][swanX] = true;
int answer = 0;
while (!Check(lake, canMove, visited))
{
Melt(lake, water);
answer++;
}
cout << answer;
return 0;
}
문제 설명
두 마리의 백조가 호수에서 살고 있었다. 그렇지만 두 마리는 호수를 덮고 있는 빙판으로 만나지 못한다.
호수는 행이 R개, 열이 C개인 직사각형 모양이다. 어떤 칸은 얼음으로 덮여있다.
호수는 차례로 녹는데, 매일 물 공간과 접촉한 모든 빙판 공간은 녹는다. 두 개의 공간이 접촉하려면 가로나 세로로 닿아 있는 것만 (대각선은 고려하지 않는다) 생각한다.
아래에는 세 가지 예가 있다.
...XXXXXX..XX.XXX ....XXXX.......XX .....XX..........
....XXXXXXXXX.XXX .....XXXX..X..... ......X..........
...XXXXXXXXXXXX.. ....XXX..XXXX.... .....X.....X.....
..XXXXX..XXXXXX.. ...XXX....XXXX... ....X......XX....
.XXXXXX..XXXXXX.. ..XXXX....XXXX... ...XX......XX....
XXXXXXX...XXXX... ..XXXX.....XX.... ....X............
..XXXXX...XXX.... ....XX.....X..... .................
....XXXXX.XXX.... .....XX....X..... .................
처음 첫째 날 둘째 날백조는 오직 물 공간에서 세로나 가로로만(대각선은 제외한다) 움직일 수 있다.
며칠이 지나야 백조들이 만날 수 있는 지 계산하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/3197
3197번: 백조의 호수
입력의 첫째 줄에는 R과 C가 주어진다. 단, 1 ≤ R, C ≤ 1500. 다음 R개의 줄에는 각각 길이 C의 문자열이 하나씩 주어진다. '.'은 물 공간, 'X'는 빙판 공간, 'L'은 백조가 있는 공간으로 나타낸다.
www.acmicpc.net
제한 사항
입력의 첫째 줄에는 R과 C가 주어진다. 단, 1 ≤ R, C ≤ 1500.
다음 R개의 줄에는 각각 길이 C의 문자열이 하나씩 주어진다. '.'은 물 공간, 'X'는 빙판 공간, 'L'은 백조가 있는 공간으로 나타낸다.
풀이
문제를 요약하면, 물은 ".", 빙하는 "X"로 표현한다.
물 옆에 있는 빙하는 하루가 지나면 녹는다.
백조는 빙하가 있는 칸은 지나갈 수 없다.
이러한 상황에서 두 백조가 며칠만에 만날 수 있는지 구해야 한다.
문제를 보고 BFS를 통해 해결할 수 있다고 생각했다.
하지만, 이 문제가 플레티넘인 이유는 메모리에 있었다.
일반적인 BFS를 돌리면 메모리 초과가 발생한다.
방문 여부를 체크해도 똑같다.
메모리 초과를 해결하기 위해서는 트릭이 필요하다.
우선, 입력을 받는 과정에서 물과 빙하, 백조의 위치까지 분리할 수 있다.
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
cin >> lake[i][j];
if (lake[i][j] == '.' || lake[i][j] == 'L') water.push({i, j});
if (lake[i][j] == 'L' && canMove.empty()) canMove.push({ i, j });
}
}백조는 하나만 있어도 다른 백조에 도달할 수 있기 때문에 하나만 관리한다.
둘째로, 빙하가 녹아내리는 과정을 트래킹하며 테두리만 큐에 담아 관리해야 한다.
입력과정에서 모든 물(.)을 큐에 담아두었다.
어떤 부분이 빙하와 인접해있는지 모르기 때문이다.
따라서, 처음에는 모든 물을 검사하여 사방에 빙하가 있다면 그 빙하는 녹아내리고 녹은 빙하가 물의 테두리가 된다.

물과 인접한 빙하는 이번에 녹아내리고 녹아내린 빙하가 물의 테두리가 되어 다음날에 인접한 빙하를 녹인다.
즉, 모든 물을 큐에 담아둘 필요없이 테두리만 큐로 관리하면 된다.
void Melt(vector<vector<char>>& lake, queue<pair<int, int>>& water)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
int waterCnt = water.size();
while (waterCnt--)
{
auto [y, x] = water.front();
water.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (lake[newY][newX] == 'X')
{
lake[newY][newX] = '.';
water.push({ newY, newX });
}
}
}
}
셋째로, 두 백조가 만나는지에 대해 체크하는 부분 역시 BFS로 구할 수 있지만 메모리 초과 때문에 위와 같은 트릭을 써야 한다.
이번에는 백조가 움직일 수 있는 부분의 끝만 트래킹하면 된다.
즉, 백조가 움직이다가 빙하를 만나는 지점은 다음날에 녹아내리며 백조가 움직일 수 있는 끝부분이 된다.

다음날부터는 백조가 움직일 수 있는 끝부분에서 BFS를 시작하면 된다.
이미 지나온 길은 다시 확인할 필요없기 때문이다.
bool Check(vector<vector<char>>& lake, queue<pair<int,int>>& canMove, vector<vector<bool>>& visited)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
queue<pair<int, int>> nextCanMove;
while (!canMove.empty())
{
auto [y, x] = canMove.front();
canMove.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
if (lake[newY][newX] == 'X')
{
nextCanMove.push({ newY, newX });
continue;
}
if (lake[newY][newX] == 'L') return true;
canMove.push({ newY, newX });
}
}
canMove = move(nextCanMove);
return false;
}
전체 코드
#include <stdio.h>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;
bool Check(vector<vector<char>>& lake, queue<pair<int,int>>& canMove, vector<vector<bool>>& visited)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
queue<pair<int, int>> nextCanMove;
while (!canMove.empty())
{
auto [y, x] = canMove.front();
canMove.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
if (lake[newY][newX] == 'X')
{
nextCanMove.push({ newY, newX });
continue;
}
if (lake[newY][newX] == 'L') return true;
canMove.push({ newY, newX });
}
}
canMove = move(nextCanMove);
return false;
}
void Melt(vector<vector<char>>& lake, queue<pair<int, int>>& water)
{
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
int waterCnt = water.size();
while (waterCnt--)
{
auto [y, x] = water.front();
water.pop();
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= lake.size() || newX < 0 || newX >= lake[0].size()) continue;
if (lake[newY][newX] == 'X')
{
lake[newY][newX] = '.';
water.push({ newY, newX });
}
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int R, C;
cin >> R >> C;
vector<vector<char>> lake(R, vector<char>(C, 0));
vector<vector<bool>> visited(R, vector<bool>(C, false));
queue<pair<int, int>> canMove;
queue<pair<int, int>> water;
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
cin >> lake[i][j];
if (lake[i][j] == '.' || lake[i][j] == 'L') water.push({i, j});
if (lake[i][j] == 'L' && canMove.empty()) canMove.push({ i, j });
}
}
auto [swanY, swanX] = canMove.front();
visited[swanY][swanX] = true;
int answer = 0;
while (!Check(lake, canMove, visited))
{
Melt(lake, water);
answer++;
}
cout << answer;
return 0;
}