백준 10868 - 최솟값

 

 

문제 설명

N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.

여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최솟값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.

https://www.acmicpc.net/problem/10868

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, (a, b)구간의 최솟값을 구하는 쿼리를 M번 수행하면 된다.

M이 최대 100,000이기 때문에 $O(N^2)$으로는 시간 초과가 발생한다.

 

해당 문제는 세그먼트 트리를 이용하면 쉽게 풀 수 있다.

세그먼트 트리란, 원래의 배열을 리프 노드로 하는 이진 트리를 말한다.

각 부모 노드는 자식 노드에 대한 쿼리를 진행한 결과를 기록하면 된다.

해당 문제에서는 최솟값을 구하는 쿼리를 요구하므로 부모 노드에 최솟값을 기록하면 된다.

 

예를 들어 보자.

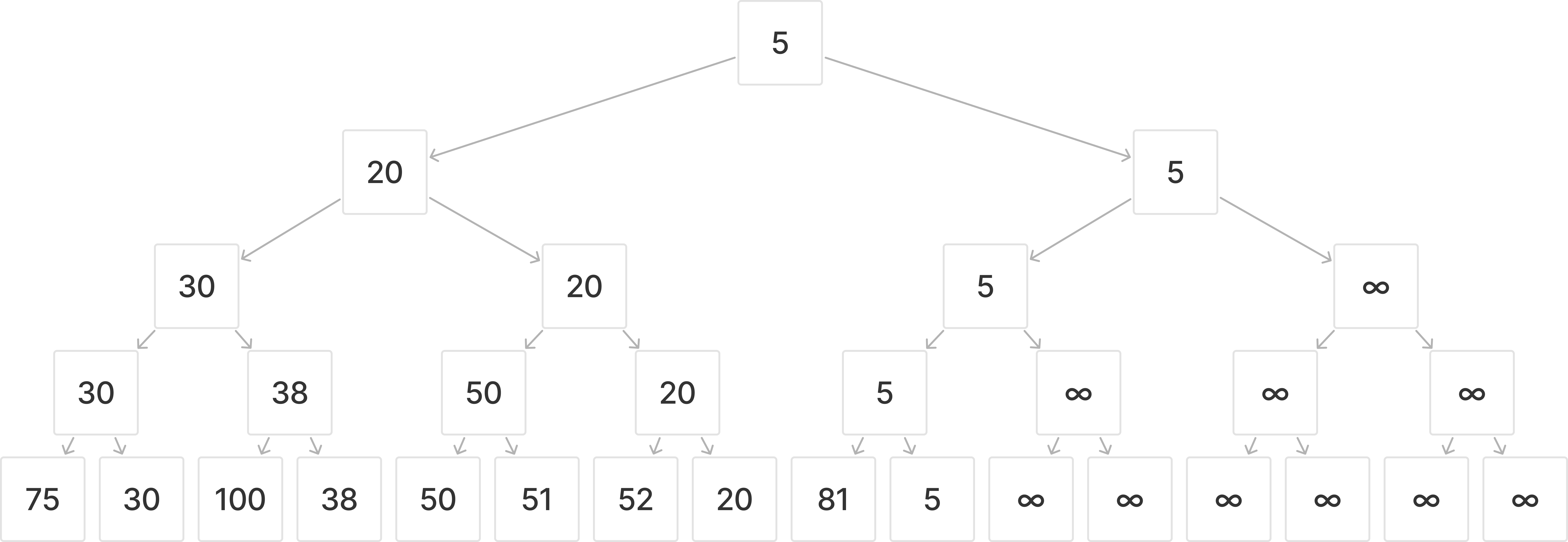
세그먼트 트리는 포화 이진 트리이기 때문에 $2^k$개의 리프노트가 필요하다.

이렇게 구성된 트리는 다음과 같은 특징을 갖는다.

• 왼쪽 자식: 2 * k
• 오른쪽 자식: 2 * k + 1
• 부모: k / 2

 

세그먼트 트리는 쿼리를 자식에 대해서만 처리한 뒤 루트 노드까지 진행하기 때문에 쿼리를 $O(logN)$안에 처리할 수 있다는 것이다.

또한, 리프 노드를 갱신하는 것도 $O(logN)$안에 처리할 수 있다.

이 역시, 자신의 부모로만 전달하면 되기 때문이다.

 

우선 노드의 상태를 업데이트하는 함수부터 봐 보자.

void update(int idx)
{
    int converted = (idx + leafSize) / 2;

    while (converted >= 1)
    {
        seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
        converted /= 2;
    }
}

리프 노드의 사이즈만큼 인덱스를 옮긴 뒤, 루트까지 갱신하면 된다.

 

쿼리를 처리하는 함수는 다음과 같다.

int getMin(int a, int b)
{
    int left = a + leafSize;
    int right = b + leafSize;

    int result = INT_MAX;
    while (left <= right)
    {
        if (left % 2 == 1) result = min(result, seg[left++]);
        if (right % 2 == 0) result = min(result, seg[right--]);

        left /= 2;
        right /= 2;
    }

    return result;
}

왼쪽 인덱스가 홀수라면 해당 노드의 부모는 (a, b)에 포함하지 않는 a-1까지 포함하여 계산하게 된다. 

따라서, 미리 계산한 뒤 부모로 옮긴다.

오른쪽 인덱스는 반대로 생각하면 된다. 

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N, M;
vector<int> nums;
vector<int> seg;
int leafSize = 1;

void update(int idx)
{
    int converted = (idx + leafSize) / 2;

    while (converted >= 1)
    {
        seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
        converted /= 2;
    }
}

int getMin(int a, int b)
{
    int left = a + leafSize;
    int right = b + leafSize;

    int result = INT_MAX;
    while (left <= right)
    {
        if (left % 2 == 1) result = min(result, seg[left++]);
        if (right % 2 == 0) result = min(result, seg[right--]);

        left /= 2;
        right /= 2;
    }

    return result;
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cout << fixed;
    cout.precision(4);

    cin >> N >> M;

    while (leafSize < N)
    {
        leafSize *= 2;
    }

    seg.resize(2 * leafSize + 1, INT_MAX);
    nums.resize(N + 1);
    for (int i = 1; i <= N; i++)
    {
        cin >> nums[i];
        seg[leafSize + i] = nums[i];
    }

    for (int i = 1; i <= N; i += 2)
    {
        update(i);
    }

    vector<pair<int, int>> querise;
    for (int i = 0; i < M; i++)
    {
        int a, b;
        cin >> a >> b;

        cout << getMin(a, b) << "\n";
    }

    return 0;
}

---