합성곱
합성곱(convolution) 연산과 교차 상관(cross-correlation) 연산에 대해 알아야 한다.
합성곱은 두 함수에 적용하여 새로운 함수를 만드는 수학 연산자이다.
합성곱은 글보다는 그림으로 이해하는 것이 쉽다.
배열 뒤집기
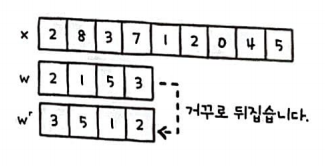
두 배열 x와 w가 있다고 가정하고 두 배열 중 원소수가 적은 배열 w의 원소 준서를 뒤집어 보면 위와 같다.
뒤집은 배열은 reverse의 약자인 r을 사용하여 w^r이라고 표현한다.
첫 번째 합성곱

왼쪽 끝자리에 맞춰 놓고 원소끼리 곱한 후 더한다.
즉, 점 곱 연산을 수행한다.
두 번째 합성곱

w^r을 오른쪽으로 한 칸 이동하여 각 배열 원소끼리 곱한 후 더한다.
나머지 합성곱
같은 방식으로 오른쪽 끝에 도착할 때까지 수행한다.

이것이 합성 곱이다.
수식으로 x * w와 같이 표기한다. 파이썬의 곱셈 연산자와 같은 기호로 표기하지만 다른 연산을 의미한다.
합성곱 구현
합성곱을 구현해 보자.
넘파이 배열 정의하고 배열 뒤집기
import numpy as np
w = np.array([2, 1, 5, 3])
x = np.array([2, 8, 3, 7, 1, 2, 0, 4, 5])
w_r = np.flip(w)
print(w_r)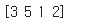
넘파이 점 곱으로 합성곱 수행
for i in range(6):
print(np.dot(x[i:i+4], w_r))
싸이파이로 합성곱 수행
싸이파이는 합성곱을 위한 함수 convolve()를 제공한다.
from scipy.signal import convolve
convolve(x, w, mode='valid')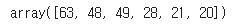
교차 상관
교차 상관은 합성곱과 동일한 방법으로 연산이 진행되지만 '미끄러지는 배열을 뒤집지 않는다'는 점이 다르다.

교차 상관 역시 싸이파이의 correlate() 함수를 사용하면 간단히 계산할 수 있다.
from scipy.signal import correlate
correlate(x, w, mode='valid')
모델을 훈련할 때 가중치 배열을 초기화하는 과정을 생각해 보면 그 이유를 짐작할 수 있다
- 가중치를 무작위 값으로 초기화
- 모든 샘플에 대하여 정방향과 역방향 계산을 수행하여 가중치를 조금씩 업데이트
모델을 훈련할 때 가중치를 무작위로 초기화하기 때문에 뒤집지 않고 적용해도 상관이 없다.
패딩과 스트라이드
패딩(padding)은 이름에서 유추할 수 있듯이 원본 개열의 양 끝에 빈 원소를 추가하는 것을 말하고, 스트라이드(stride)는 미끄러지는 배열의 간격을 조절하는 것을 말한다.
이 두 개념이 어떻게 적용되는지에 따라 밸리드 패딩, 풀 패딩, 세임 패딩이라고 부른다.
밸리드 패딩
교차 상관을 싸이파이로 구현할 때 mode 매개변수에 'valid'를 지정했다.
바로 이것이 밸리드 패딩(valid paaing)이다.
밸리드 패딩은 원본 배열에 패딩을 추가하지 않고 미끄러지는 배열이 원본 배열의 끝으로 갈 때까지 교차 상관을 수행한다. 이로 인해 밸리드 패딩의 결과로 얻는 배열의 크기는 원본 배열보다 항상 작다.
밸리드 패딩의 특징은 원본 배열의 각 원소가 연산에 참여하는 정도가 다르다.
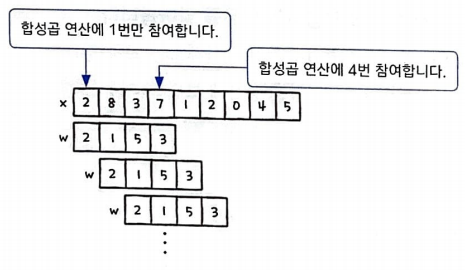
풀 패딩
원본 배열의 원소가 연산에 동일하게 참여하려면 원본 배열의 양 끝에 가장의 원소를 추가해야 한다.
이때 가상의 원소로 0을 사용하면 이를 제로 패딩(zero padding)이라고 부른다.
적절한 개수의 제로 패딩을 추가하면 원본 배열의 모든 원소가 동일하게 연산에 참여하게 만들 수 있다.
이를 풀 패딩(full padding)이라고 한다.
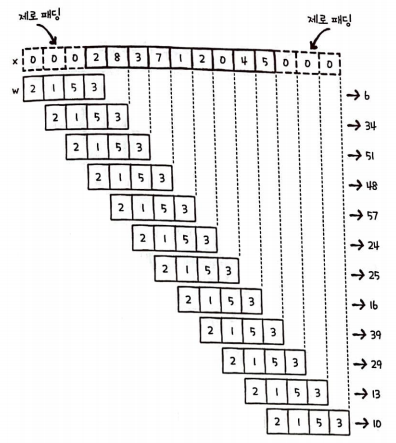
correlate() 함수에서 풀 패딩을 적용하려면 mode를 full로 적용하면 된다.
correlate(x, w, mode='full')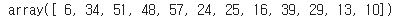
세임 패딩
세임 패딩(same padding)은 출력 배열의 길이가 원본 배열의 길이와 같아지도록 원본 배열에 제로 패딩을 추가하는 것이다.

원본 배열의 길이가 9이므로 원본 배열 왼쪽 끝에 2개, 오른쪽 끝에는 1개를 패딩 한다.
따라서 출력이 9개가 나온다. mode를 same으로 적용하면 된다.
correlate(x, w, mode='same')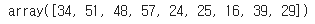
스트라이드
스트라이드는 미끄러지는 간격을 조정한다.
지금까지는 스트라이드가 1이라 1칸씩 미끄러지며 연산을 수행했다.
만약 스트라이드를 2로 지정하면 2칸씩 미끄러지며 연산을 수행한다.

합성곱 신경망을 만들 때는 보통 스트라이드를 1로 지정한다.
합성곱 신경망은 대부분 2차원 배열에 대한 합성곱을 사용한다.
2차원 배열 합성곱
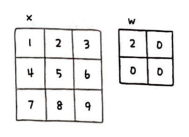
위와 같은 2차원 배열이 있다고 가정하자.
원본 배열(x)의 왼쪽 모서리 끝에 미끄러지는 배열을 맞춘 다음 합성곱을 수행한다.
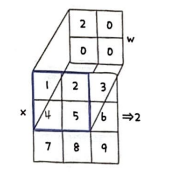
오른쪽으로 진행하다 끝에 도착하면 아래로 1칸 내린 다음 다시 왼쪽부터 합성곱을 수행한다.

싸이파이의 correlate2d() 함수를 사용할 수 있다.
x = np.arange(1,10,dtype=int)
x = x.reshape((3,3))
print(x)
w = np.array([[2, 0], [0, 0]])
print(w)
from scipy.signal import correlate2d
correlate2d(x, w, mode='valid')

위와 같이 진행하려면 same padding을 사용해야 한다.
from scipy.signal import correlate2d
correlate2d(x, w, mode='same')
텐서플로로 합성곱을 수행해보자.
합성곱 신경망의 입력은 일반적으로 4차원 배열이다.
텐서플로에서 2차원 합성곱을 수행하는 함수는 conv2d()이다.
입력 이미지의 높이와 너비 외에 더 많은 차원을 필요하기 때문이다.

샘플은 R, G, B로 구분되는 3개의 컬러 채널을 가지고 있다.
위 입력을 4차원 배열로 표현하면 (2, 3, 3, 3)이다.
각 숫자는 배치, 샘플의 높이, 샘플의 너비, 컬러 채널의 차원을 의미한다.
입력과 곱해지는 가중치도 4개의 차원으로 구성된다.
첫 번째, 두 번째 차원은 가중치의 높이와 너비이고 세 번째 차원은 채널이며 네 번째 차원이 가중치의 개수이다.
다음의 경우 (2, 2, 3, 3)으로 표현한다.

입력과 가중치에 세임 패딩을 적용하여 합성곱을 수행하면 (입력의 배치, 입력의 높이, 입력의 너비, 가중치의 개수)가 된다.

코드로 구현해보자.
import tensorflow as tf
x_4d = x.astype(np.float).reshape(1, 3, 3, 1)
w_4d = w.reshape(2, 2, 1, 1)
print(x_4d)
print(w_4d)
스트라이드는 1, 패딩은 세임 패딩을 적용한다.
c_out = tf.nn.conv2d(x_4d, w_4d, strides=1, padding='SAME')
c_out.numpy().reshape(3, 3)
합성곱
합성곱(convolution) 연산과 교차 상관(cross-correlation) 연산에 대해 알아야 한다.
합성곱은 두 함수에 적용하여 새로운 함수를 만드는 수학 연산자이다.
합성곱은 글보다는 그림으로 이해하는 것이 쉽다.
배열 뒤집기

두 배열 x와 w가 있다고 가정하고 두 배열 중 원소수가 적은 배열 w의 원소 준서를 뒤집어 보면 위와 같다.
뒤집은 배열은 reverse의 약자인 r을 사용하여 w^r이라고 표현한다.
첫 번째 합성곱

왼쪽 끝자리에 맞춰 놓고 원소끼리 곱한 후 더한다.
즉, 점 곱 연산을 수행한다.
두 번째 합성곱

w^r을 오른쪽으로 한 칸 이동하여 각 배열 원소끼리 곱한 후 더한다.
나머지 합성곱
같은 방식으로 오른쪽 끝에 도착할 때까지 수행한다.

이것이 합성 곱이다.
수식으로 x * w와 같이 표기한다. 파이썬의 곱셈 연산자와 같은 기호로 표기하지만 다른 연산을 의미한다.
합성곱 구현
합성곱을 구현해 보자.
넘파이 배열 정의하고 배열 뒤집기
import numpy as np
w = np.array([2, 1, 5, 3])
x = np.array([2, 8, 3, 7, 1, 2, 0, 4, 5])
w_r = np.flip(w)
print(w_r)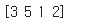
넘파이 점 곱으로 합성곱 수행
for i in range(6):
print(np.dot(x[i:i+4], w_r))
싸이파이로 합성곱 수행
싸이파이는 합성곱을 위한 함수 convolve()를 제공한다.
from scipy.signal import convolve
convolve(x, w, mode='valid')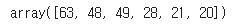
교차 상관
교차 상관은 합성곱과 동일한 방법으로 연산이 진행되지만 '미끄러지는 배열을 뒤집지 않는다'는 점이 다르다.

교차 상관 역시 싸이파이의 correlate() 함수를 사용하면 간단히 계산할 수 있다.
from scipy.signal import correlate
correlate(x, w, mode='valid')
모델을 훈련할 때 가중치 배열을 초기화하는 과정을 생각해 보면 그 이유를 짐작할 수 있다
- 가중치를 무작위 값으로 초기화
- 모든 샘플에 대하여 정방향과 역방향 계산을 수행하여 가중치를 조금씩 업데이트
모델을 훈련할 때 가중치를 무작위로 초기화하기 때문에 뒤집지 않고 적용해도 상관이 없다.
패딩과 스트라이드
패딩(padding)은 이름에서 유추할 수 있듯이 원본 개열의 양 끝에 빈 원소를 추가하는 것을 말하고, 스트라이드(stride)는 미끄러지는 배열의 간격을 조절하는 것을 말한다.
이 두 개념이 어떻게 적용되는지에 따라 밸리드 패딩, 풀 패딩, 세임 패딩이라고 부른다.
밸리드 패딩
교차 상관을 싸이파이로 구현할 때 mode 매개변수에 'valid'를 지정했다.
바로 이것이 밸리드 패딩(valid paaing)이다.
밸리드 패딩은 원본 배열에 패딩을 추가하지 않고 미끄러지는 배열이 원본 배열의 끝으로 갈 때까지 교차 상관을 수행한다. 이로 인해 밸리드 패딩의 결과로 얻는 배열의 크기는 원본 배열보다 항상 작다.
밸리드 패딩의 특징은 원본 배열의 각 원소가 연산에 참여하는 정도가 다르다.

풀 패딩
원본 배열의 원소가 연산에 동일하게 참여하려면 원본 배열의 양 끝에 가장의 원소를 추가해야 한다.
이때 가상의 원소로 0을 사용하면 이를 제로 패딩(zero padding)이라고 부른다.
적절한 개수의 제로 패딩을 추가하면 원본 배열의 모든 원소가 동일하게 연산에 참여하게 만들 수 있다.
이를 풀 패딩(full padding)이라고 한다.

correlate() 함수에서 풀 패딩을 적용하려면 mode를 full로 적용하면 된다.
correlate(x, w, mode='full')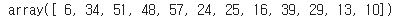
세임 패딩
세임 패딩(same padding)은 출력 배열의 길이가 원본 배열의 길이와 같아지도록 원본 배열에 제로 패딩을 추가하는 것이다.

원본 배열의 길이가 9이므로 원본 배열 왼쪽 끝에 2개, 오른쪽 끝에는 1개를 패딩 한다.
따라서 출력이 9개가 나온다. mode를 same으로 적용하면 된다.
correlate(x, w, mode='same')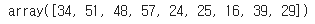
스트라이드
스트라이드는 미끄러지는 간격을 조정한다.
지금까지는 스트라이드가 1이라 1칸씩 미끄러지며 연산을 수행했다.
만약 스트라이드를 2로 지정하면 2칸씩 미끄러지며 연산을 수행한다.

합성곱 신경망을 만들 때는 보통 스트라이드를 1로 지정한다.
합성곱 신경망은 대부분 2차원 배열에 대한 합성곱을 사용한다.
2차원 배열 합성곱

위와 같은 2차원 배열이 있다고 가정하자.
원본 배열(x)의 왼쪽 모서리 끝에 미끄러지는 배열을 맞춘 다음 합성곱을 수행한다.

오른쪽으로 진행하다 끝에 도착하면 아래로 1칸 내린 다음 다시 왼쪽부터 합성곱을 수행한다.

싸이파이의 correlate2d() 함수를 사용할 수 있다.
x = np.arange(1,10,dtype=int)
x = x.reshape((3,3))
print(x)
w = np.array([[2, 0], [0, 0]])
print(w)
from scipy.signal import correlate2d
correlate2d(x, w, mode='valid')

위와 같이 진행하려면 same padding을 사용해야 한다.
from scipy.signal import correlate2d
correlate2d(x, w, mode='same')
텐서플로로 합성곱을 수행해보자.
합성곱 신경망의 입력은 일반적으로 4차원 배열이다.
텐서플로에서 2차원 합성곱을 수행하는 함수는 conv2d()이다.
입력 이미지의 높이와 너비 외에 더 많은 차원을 필요하기 때문이다.

샘플은 R, G, B로 구분되는 3개의 컬러 채널을 가지고 있다.
위 입력을 4차원 배열로 표현하면 (2, 3, 3, 3)이다.
각 숫자는 배치, 샘플의 높이, 샘플의 너비, 컬러 채널의 차원을 의미한다.
입력과 곱해지는 가중치도 4개의 차원으로 구성된다.
첫 번째, 두 번째 차원은 가중치의 높이와 너비이고 세 번째 차원은 채널이며 네 번째 차원이 가중치의 개수이다.
다음의 경우 (2, 2, 3, 3)으로 표현한다.

입력과 가중치에 세임 패딩을 적용하여 합성곱을 수행하면 (입력의 배치, 입력의 높이, 입력의 너비, 가중치의 개수)가 된다.

코드로 구현해보자.
import tensorflow as tf
x_4d = x.astype(np.float).reshape(1, 3, 3, 1)
w_4d = w.reshape(2, 2, 1, 1)
print(x_4d)
print(w_4d)
스트라이드는 1, 패딩은 세임 패딩을 적용한다.
c_out = tf.nn.conv2d(x_4d, w_4d, strides=1, padding='SAME')
c_out.numpy().reshape(3, 3)
