문제
주어진 두 원 사이에 있는 정수의 점의 개수를 구하는 문제이다.
원의 방정식을 이용하여 쉽게 풀 수 있다.
제한 사항을 보면 주어지는 원의 반지름(r)이 꽤 크다.
따라서, 완전 탐색은 불가능하다고 판단했다.
문제 설명
x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해 주세요.
※ 각 원 위의 점도 포함하여 셉니다.
https://school.programmers.co.kr/learn/courses/30/lessons/181187#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
제한 사항
- 1 ≤ r1 < r2 ≤ 1,000,000
풀이
x의 값을 설정하면 두 원의 점 y1, y2를 알 수 있다.
원의 방정식을 이용하면 된다.
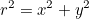
long double y1 = x < r1 ? sqrt((long long)r1*r1 - (long long)x*x) : 0;
long double y2 = sqrt((long long)r2*r2 - (long long)x*x);작은 원의 범위를 넘어가는 부분도 탐색해야 하기 때문에 범위를 넘어가면 0으로 대체한다.
y의 값을 구한 후 y1 ~ y2 사이에 있는 점을 구하면 된다.
그러기 위해 y1의 값은 올림하고 y2의 값은 내림하여 값을 조정한다.
// 정수로 조정
y1 = ceil(y1);
y2 = floor(y2);
작은 원의 y가 0이 되는 지점에서 점의 개수가 달라진다.
이전에는 x축을 기준으로 대칭적으로 존재하지만 이 부분부터는 축에 닿는 부분은 1개의 점만 존재하기 때문에 식을 다르게 작성해야 한다.
if(x < r1)
{
answer += (y2 - y1 + 1) * 4;
}
else
{
answer += (y2 - y1) * 4 + 2;
}
이러한 과정을 x가 1부터 r2가 되기 전까지 반복하여 답을 구하면 된다.
이때, x축과 y축에 있는 점들은 제외하고 계산한다. (계산하는 법이 다르기 때문이다.)
계산이 끝난 후 경곗값 부분을 처리하면 된다.
// y = 0 (r2)
answer += 2;
// x = 0
answer += (r2 - r1 + 1) * 2;
전체 코드
#include <string>
#include <vector>
#include <cmath>
using namespace std;
long long solution(int r1, int r2) {
long long answer = 0;
// x의 값을 설정하면 두 원의 점 y1, y2를 알 수 있음
// y1 ~ y2 사이 점을 구함
// 원의 방정식: r^2 = x^2 + y^2
// 경계값은 제외
for(int x = 1; x < r2; x++)
{
long double y1 = x < r1 ? sqrt((long long)r1*r1 - (long long)x*x) : 0;
long double y2 = sqrt((long long)r2*r2 - (long long)x*x);
// 정수로 조정
y1 = ceil(y1);
y2 = floor(y2);
if(x < r1)
{
answer += (y2 - y1 + 1) * 4;
}
else
{
answer += (y2 - y1) * 4 + 2;
}
}
// y = 0 (r2)
answer += 2;
// x = 0
answer += (r2 - r1 + 1) * 2;
return answer;
}
문제
주어진 두 원 사이에 있는 정수의 점의 개수를 구하는 문제이다.
원의 방정식을 이용하여 쉽게 풀 수 있다.
제한 사항을 보면 주어지는 원의 반지름(r)이 꽤 크다.
따라서, 완전 탐색은 불가능하다고 판단했다.
문제 설명
x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해 주세요.
※ 각 원 위의 점도 포함하여 셉니다.
https://school.programmers.co.kr/learn/courses/30/lessons/181187#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
제한 사항
- 1 ≤ r1 < r2 ≤ 1,000,000
풀이
x의 값을 설정하면 두 원의 점 y1, y2를 알 수 있다.
원의 방정식을 이용하면 된다.
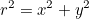
long double y1 = x < r1 ? sqrt((long long)r1*r1 - (long long)x*x) : 0;
long double y2 = sqrt((long long)r2*r2 - (long long)x*x);작은 원의 범위를 넘어가는 부분도 탐색해야 하기 때문에 범위를 넘어가면 0으로 대체한다.
y의 값을 구한 후 y1 ~ y2 사이에 있는 점을 구하면 된다.
그러기 위해 y1의 값은 올림하고 y2의 값은 내림하여 값을 조정한다.
// 정수로 조정
y1 = ceil(y1);
y2 = floor(y2);
작은 원의 y가 0이 되는 지점에서 점의 개수가 달라진다.
이전에는 x축을 기준으로 대칭적으로 존재하지만 이 부분부터는 축에 닿는 부분은 1개의 점만 존재하기 때문에 식을 다르게 작성해야 한다.
if(x < r1)
{
answer += (y2 - y1 + 1) * 4;
}
else
{
answer += (y2 - y1) * 4 + 2;
}
이러한 과정을 x가 1부터 r2가 되기 전까지 반복하여 답을 구하면 된다.
이때, x축과 y축에 있는 점들은 제외하고 계산한다. (계산하는 법이 다르기 때문이다.)
계산이 끝난 후 경곗값 부분을 처리하면 된다.
// y = 0 (r2)
answer += 2;
// x = 0
answer += (r2 - r1 + 1) * 2;
전체 코드
#include <string>
#include <vector>
#include <cmath>
using namespace std;
long long solution(int r1, int r2) {
long long answer = 0;
// x의 값을 설정하면 두 원의 점 y1, y2를 알 수 있음
// y1 ~ y2 사이 점을 구함
// 원의 방정식: r^2 = x^2 + y^2
// 경계값은 제외
for(int x = 1; x < r2; x++)
{
long double y1 = x < r1 ? sqrt((long long)r1*r1 - (long long)x*x) : 0;
long double y2 = sqrt((long long)r2*r2 - (long long)x*x);
// 정수로 조정
y1 = ceil(y1);
y2 = floor(y2);
if(x < r1)
{
answer += (y2 - y1 + 1) * 4;
}
else
{
answer += (y2 - y1) * 4 + 2;
}
}
// y = 0 (r2)
answer += 2;
// x = 0
answer += (r2 - r1 + 1) * 2;
return answer;
}
