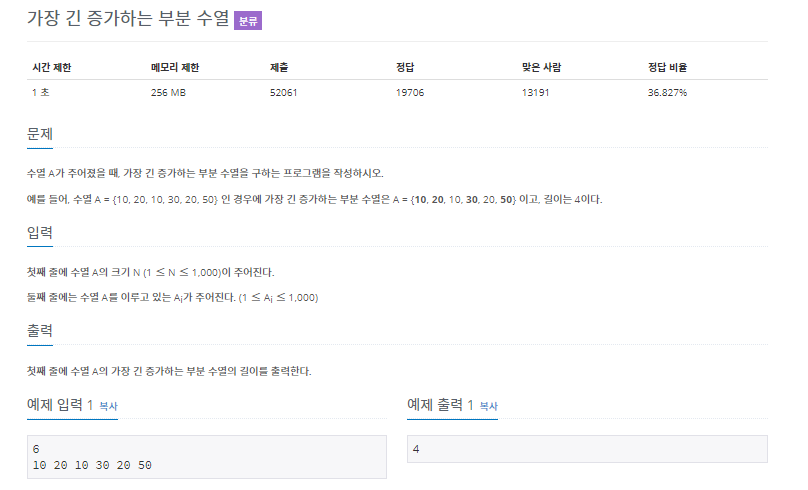
증가하는 수열을 만드는 문제이다. 기준을 정해서 그 부분까지의 가장 긴 부분 수열을 구하는 문제로 분할할 수 있다.
즉 i번째까지의 가장 긴 증가하는 수열을 저장해놓고 계속해서 사용하며 마지막까지 수열을 구해 나간다.
다음은 Java로 작성한 코드이다.
import java.util.Scanner;
public class partSequence {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int x = scan.nextInt();
//수열 저장
int arr[] = new int[x];
//가장 긴 증가하는 수열의 수
int solution[] = new int[x];
//입력을 받는 동시에 solution을 모두 1로 초기화
for( int i = 0 ; i < x ; i++ ) {
arr[i] = scan.nextInt();
solution[i] = 1;
}
//수열 계산
for( int i = 0 ; i < x ; i++ ) {
for(int j = 0 ; j <= i ; j++) {
if( arr[j] < arr[i] && solution[i] <= solution[j]) {
solution[i] = solution[j]+1;
}
}
}
int max = 0;
//가장 큰 수열을 찾아 출력
for( int i = 0 ; i < x ; i++ ) {
max = Math.max(max, solution[i]);
}
System.out.println(max);
}
}
arr[]은 수열을 입력받아 저장하는 배열이고, solution[]은 i번째까지의 가장 긴 증가하는 수열의 수를 저장해 놓는 배열이다. 우선, solution[]을 모두 1로 초기화 한다.
i번까지의 가장 긴 증가하는 수열을 구하는 과정에서 j번째 수가 i번째 수보다 작고, j번째 solution이 i번째 solution보다 크거나 같으면 solution[j]에 1을 더해 solution[i]에 저장한다.
(solution[j]에는 j까지의 가장 긴 증가하는 수열의 수가 저장되어 있고, i번째 수가 더 크기때문에 수열에 i까지 합할 수 있기 때문이다.)
마지막까지 수열의 수를 구한 후, 저장되어 있는 solution중 제일 큰 수를 찾아 출력한다.
