문제 설명
Ax + By + C = 0으로 표현할 수 있는 n개의 직선이 주어질 때, 이 직선의 교점 중 정수 좌표에 별을 그리려 합니다.
예를 들어, 다음과 같은 직선 5개를
- 2x - y + 4 = 0
- -2x - y + 4 = 0
- -y + 1 = 0
- 5x - 8y - 12 = 0
- 5x + 8y + 12 = 0
좌표 평면 위에 그리면 아래 그림과 같습니다.
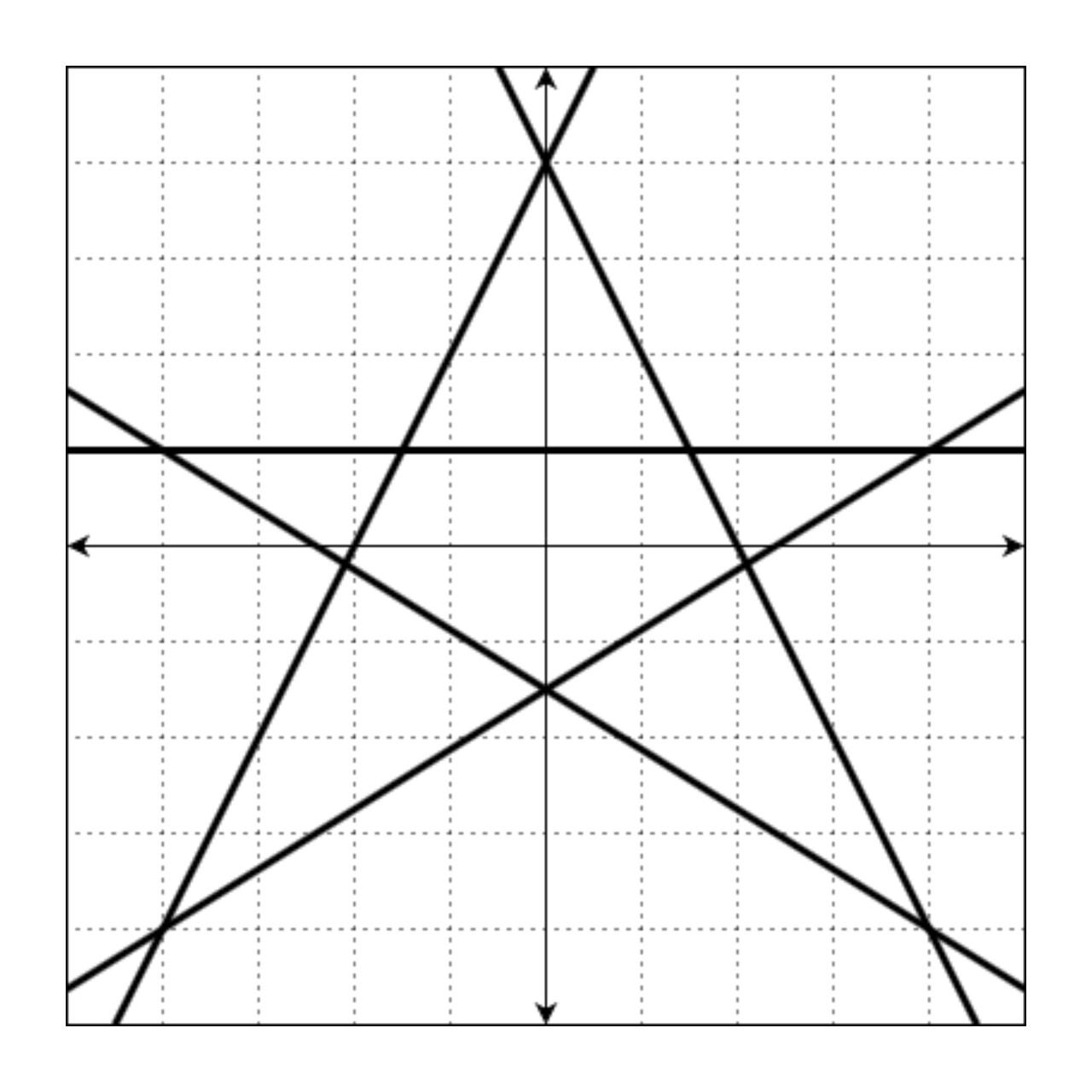
이때, 모든 교점의 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4), (1.5, 1.0), (2.1, -0.19), (0, -1.5), (-2.1, -0.19), (-1.5, 1.0)입니다. 이 중 정수로만 표현되는 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4)입니다.
만약 정수로 표현되는 교점에 별을 그리면 다음과 같습니다.
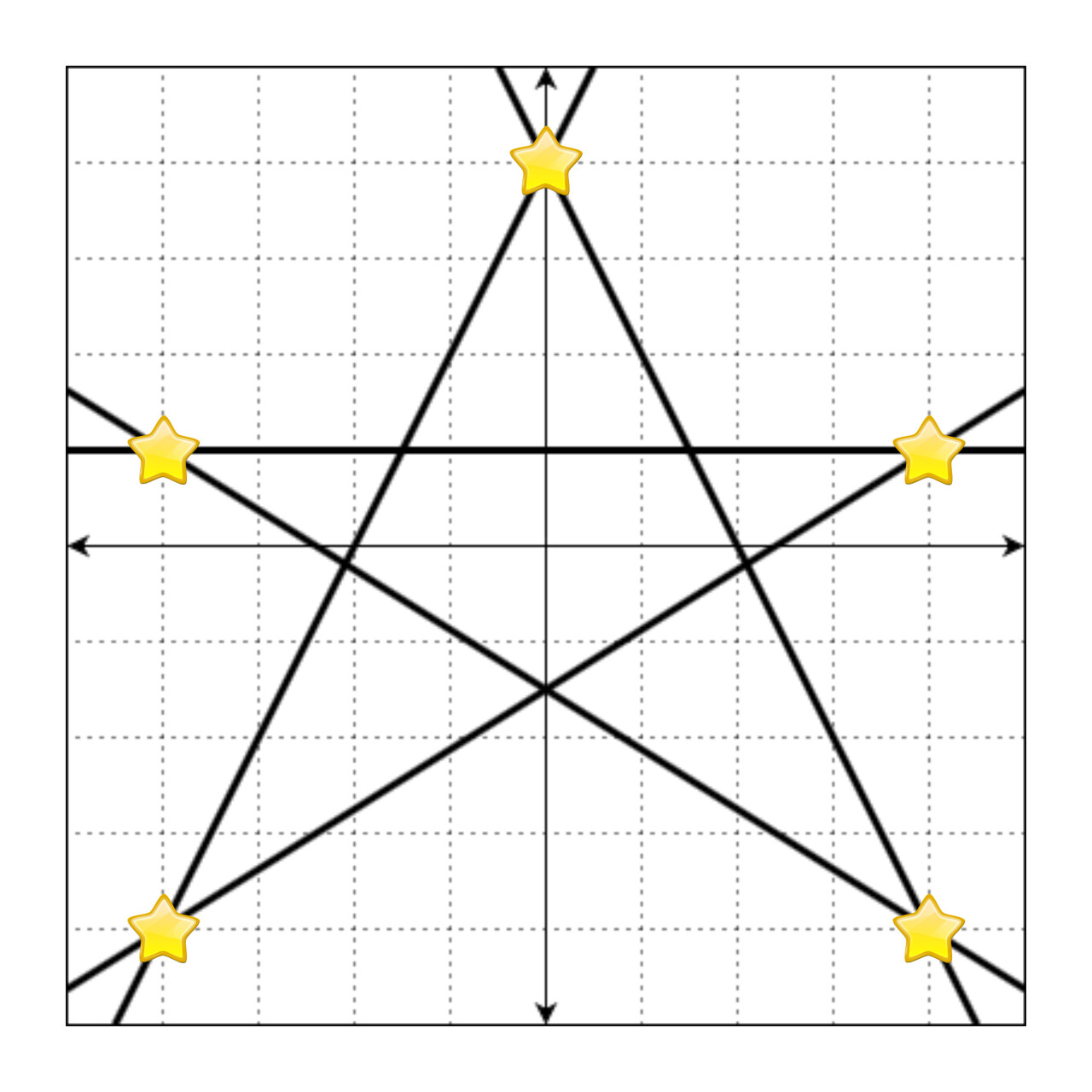
위의 그림을 문자열로 나타낼 때, 별이 그려진 부분은 *, 빈 공간(격자선이 교차하는 지점)은 .으로 표현하면 다음과 같습니다.
"..........."
".....*....."
"..........."
"..........."
".*.......*."
"..........."
"..........."
"..........."
"..........."
".*.......*."
"..........."이때 격자판은 무한히 넓으니 모든 별을 포함하는 최소한의 크기만 나타내면 됩니다.
따라서 정답은
"....*...."
"........."
"........."
"*.......*"
"........."
"........."
"........."
"........."
"*.......*"입니다.
직선 A, B, C에 대한 정보가 담긴 배열 line이 매개변수로 주어집니다. 이때 모든 별을 포함하는 최소 사각형을 return 하도록 solution 함수를 완성해주세요.
제한 사항
- line의 세로(행) 길이는 2 이상 1,000 이하인 자연수입니다.
- line의 가로(열) 길이는 3입니다.
- line의 각 원소는 [A, B, C] 형태입니다.
- A, B, C는 -100,000 이상 100,000 이하인 정수입니다.
- 무수히 많은 교점이 생기는 직선 쌍은 주어지지 않습니다.
- A = 0이면서 B = 0인 경우는 주어지지 않습니다.
- 정답은 1,000 * 1,000 크기 이내에서 표현됩니다.
- 별이 한 개 이상 그려지는 입력만 주어집니다.
풀이
임의의 두 개의 직선을 선택하여 교점을 구한 뒤 정수만을 채택한다.
임의의 두 개의 직선을 고르는 방법은 조합을 만드는 것이다.
교점을 구하는 식은 다음과 같다.
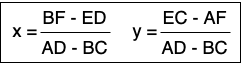
즉, 분자를 분모로 나누었을 때, 나누어 떨어지는 경우만 채택하면 된다.
그리고 좌표 평면을 최소의 범위로 잘라야 한다.
X, Y의 좌표들 중 최소, 최댓값을 구한 뒤 차이를 구하면 된다.
그 후, 각 좌표들을 배열에 맞게 이동하면 된다.
X는 최솟값의 좌표가 0이 되기 때문에 minX(X의 최솟값)을 빼주면 된다.
Y는 최댓값의 좌표가 0이 되기 때문에 maxY(Y의 최댓값)에서 각 좌표를 빼주면 된다.
long long x = p.first - minX;
long long y = maxY - p.second;
이 문제에서 주의할 부분이 있다.
계산 결과가 int안에서 표현되지 않을 경우가 있다.
따라서, long이나 long long자료형을 사용해야 한다.
또한, 최솟값, 최댓값의 초기값을 충분히 작고 충분히 크게 해주지 않으면 27, 28번 테스트에서 실패한다.
const long long MAX = 9'223'372'036'854'775'807;
전체 코드
#include <string>
#include <vector>
#include <iostream>
#include <set>
using namespace std;
const long long MAX = 9'223'372'036'854'775'807;
set<pair<long long,long long>> points;
long long minX = MAX;
long long minY = MAX;
long long maxX = -MAX;
long long maxY = -MAX;
pair<long long, long long> findPoint(vector<int> a, vector<int> b)
{
// 평행
long A = static_cast<long>(a[0]);
long B = static_cast<long>(a[1]);
long C = static_cast<long>(b[0]);
long D = static_cast<long>(b[1]);
long E = static_cast<long>(a[2]);
long F = static_cast<long>(b[2]);
long det = (A * D) - (B * C);
if(det == 0) return {MAX, MAX};
long long x = MAX;
long long y = MAX;
if(((B * F) - (E * D)) % det == 0)
{
x = ((B * F) - (E * D)) / det;
}
if(((E * C) - (A * F)) % det == 0)
{
y = ((E * C) - (A * F)) / det;
}
return {x,y};
}
void dfs(vector<vector<int>>& line, vector<vector<int>>& temp, int idx)
{
if(temp.size() == 2)
{
auto point = findPoint(temp[0], temp[1]);
if(point.first != MAX && point.second != MAX)
{
minX = min(minX, point.first);
minY = min(minY, point.second);
maxX = max(maxX, point.first);
maxY = max(maxY, point.second);
points.insert(point);
}
return;
}
for(int i = idx; i < line.size(); i++)
{
temp.push_back(line[i]);
dfs(line, temp, i+1);
temp.pop_back();
}
}
vector<string> solution(vector<vector<int>> line) {
vector<string> answer;
vector<vector<int>> temp;
dfs(line, temp, 0);
long long rangeX = maxX - minX + 1;
long long rangeY = maxY - minY + 1;
for(long long i = 0; i < rangeY; i++)
{
string row(rangeX, '.');
answer.push_back(row);
}
for(auto p : points)
{
long long x = p.first - minX;
long long y = maxY - p.second;
answer[y][x] = '*';
}
return answer;
}문제 설명
Ax + By + C = 0으로 표현할 수 있는 n개의 직선이 주어질 때, 이 직선의 교점 중 정수 좌표에 별을 그리려 합니다.
예를 들어, 다음과 같은 직선 5개를
- 2x - y + 4 = 0
- -2x - y + 4 = 0
- -y + 1 = 0
- 5x - 8y - 12 = 0
- 5x + 8y + 12 = 0
좌표 평면 위에 그리면 아래 그림과 같습니다.

이때, 모든 교점의 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4), (1.5, 1.0), (2.1, -0.19), (0, -1.5), (-2.1, -0.19), (-1.5, 1.0)입니다. 이 중 정수로만 표현되는 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4)입니다.
만약 정수로 표현되는 교점에 별을 그리면 다음과 같습니다.

위의 그림을 문자열로 나타낼 때, 별이 그려진 부분은 *, 빈 공간(격자선이 교차하는 지점)은 .으로 표현하면 다음과 같습니다.
"..........."
".....*....."
"..........."
"..........."
".*.......*."
"..........."
"..........."
"..........."
"..........."
".*.......*."
"..........."이때 격자판은 무한히 넓으니 모든 별을 포함하는 최소한의 크기만 나타내면 됩니다.
따라서 정답은
"....*...."
"........."
"........."
"*.......*"
"........."
"........."
"........."
"........."
"*.......*"입니다.
직선 A, B, C에 대한 정보가 담긴 배열 line이 매개변수로 주어집니다. 이때 모든 별을 포함하는 최소 사각형을 return 하도록 solution 함수를 완성해주세요.
제한 사항
- line의 세로(행) 길이는 2 이상 1,000 이하인 자연수입니다.
- line의 가로(열) 길이는 3입니다.
- line의 각 원소는 [A, B, C] 형태입니다.
- A, B, C는 -100,000 이상 100,000 이하인 정수입니다.
- 무수히 많은 교점이 생기는 직선 쌍은 주어지지 않습니다.
- A = 0이면서 B = 0인 경우는 주어지지 않습니다.
- 정답은 1,000 * 1,000 크기 이내에서 표현됩니다.
- 별이 한 개 이상 그려지는 입력만 주어집니다.
풀이
임의의 두 개의 직선을 선택하여 교점을 구한 뒤 정수만을 채택한다.
임의의 두 개의 직선을 고르는 방법은 조합을 만드는 것이다.
교점을 구하는 식은 다음과 같다.
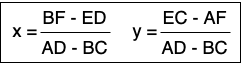
즉, 분자를 분모로 나누었을 때, 나누어 떨어지는 경우만 채택하면 된다.
그리고 좌표 평면을 최소의 범위로 잘라야 한다.
X, Y의 좌표들 중 최소, 최댓값을 구한 뒤 차이를 구하면 된다.
그 후, 각 좌표들을 배열에 맞게 이동하면 된다.
X는 최솟값의 좌표가 0이 되기 때문에 minX(X의 최솟값)을 빼주면 된다.
Y는 최댓값의 좌표가 0이 되기 때문에 maxY(Y의 최댓값)에서 각 좌표를 빼주면 된다.
long long x = p.first - minX;
long long y = maxY - p.second;
이 문제에서 주의할 부분이 있다.
계산 결과가 int안에서 표현되지 않을 경우가 있다.
따라서, long이나 long long자료형을 사용해야 한다.
또한, 최솟값, 최댓값의 초기값을 충분히 작고 충분히 크게 해주지 않으면 27, 28번 테스트에서 실패한다.
const long long MAX = 9'223'372'036'854'775'807;
전체 코드
#include <string>
#include <vector>
#include <iostream>
#include <set>
using namespace std;
const long long MAX = 9'223'372'036'854'775'807;
set<pair<long long,long long>> points;
long long minX = MAX;
long long minY = MAX;
long long maxX = -MAX;
long long maxY = -MAX;
pair<long long, long long> findPoint(vector<int> a, vector<int> b)
{
// 평행
long A = static_cast<long>(a[0]);
long B = static_cast<long>(a[1]);
long C = static_cast<long>(b[0]);
long D = static_cast<long>(b[1]);
long E = static_cast<long>(a[2]);
long F = static_cast<long>(b[2]);
long det = (A * D) - (B * C);
if(det == 0) return {MAX, MAX};
long long x = MAX;
long long y = MAX;
if(((B * F) - (E * D)) % det == 0)
{
x = ((B * F) - (E * D)) / det;
}
if(((E * C) - (A * F)) % det == 0)
{
y = ((E * C) - (A * F)) / det;
}
return {x,y};
}
void dfs(vector<vector<int>>& line, vector<vector<int>>& temp, int idx)
{
if(temp.size() == 2)
{
auto point = findPoint(temp[0], temp[1]);
if(point.first != MAX && point.second != MAX)
{
minX = min(minX, point.first);
minY = min(minY, point.second);
maxX = max(maxX, point.first);
maxY = max(maxY, point.second);
points.insert(point);
}
return;
}
for(int i = idx; i < line.size(); i++)
{
temp.push_back(line[i]);
dfs(line, temp, i+1);
temp.pop_back();
}
}
vector<string> solution(vector<vector<int>> line) {
vector<string> answer;
vector<vector<int>> temp;
dfs(line, temp, 0);
long long rangeX = maxX - minX + 1;
long long rangeY = maxY - minY + 1;
for(long long i = 0; i < rangeY; i++)
{
string row(rangeX, '.');
answer.push_back(row);
}
for(auto p : points)
{
long long x = p.first - minX;
long long y = maxY - p.second;
answer[y][x] = '*';
}
return answer;
}