문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.
- 조각은 한 번에 하나씩 채워 넣습니다.
- 조각을 회전시킬 수 있습니다.
- 조각을 뒤집을 수는 없습니다.
- 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.
다음은 퍼즐 조각을 채우는 예시입니다.
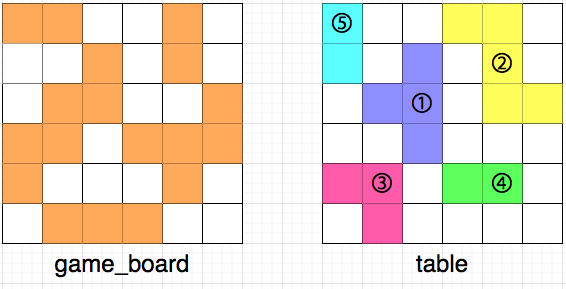
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.
이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.
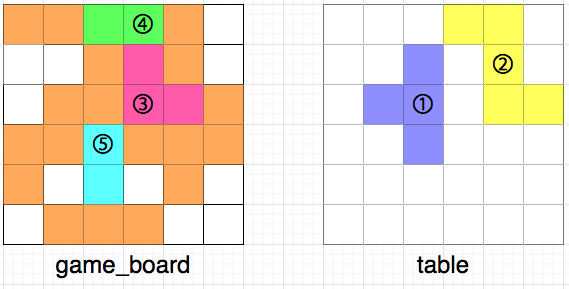
- 3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
- 5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.
다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.

최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.
현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.
https://school.programmers.co.kr/learn/courses/30/lessons/84021
제한 사항
- 3 ≤ game_board의 행 길이 ≤ 50
- game_board의 각 열 길이 = game_board의 행 길이
- 즉, 게임 보드는 정사각 격자 모양입니다.
- game_board의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 이미 채워진 칸을 나타냅니다.\퍼즐 조각이 놓일 빈칸은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- table의 행 길이 = game_board의 행 길이
- table의 각 열 길이 = table의 행 길이
- 즉, 테이블은 game_board와 같은 크기의 정사각 격자 모양입니다.
- table의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 조각이 놓인 칸을 나타냅니다.
- 퍼즐 조각은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- game_board에는 반드시 하나 이상의 빈칸이 있습니다.
- table에는 반드시 하나 이상의 블록이 놓여 있습니다.
풀이
BFS를 이용하는 문제이다.
문제풀이는 간단하다.
- 빈칸과 블록을 BFS를 통해 탐색한다.
- 블록을 회전하며 맞는 빈칸이 있는지 확인하면 된다.
우선 BFS로 빈칸과 블록을 탐색하는 것은 간단하다.
일반적인 BFS와 차이가 없기 때문이다.
이때, 탐색한 빈칸이나 블록을 board처럼 저장하지 말고 각각의 좌표를 저장한다.

4번 블록을 예로 들면, {4, 3}, {4, 4}가 된다.
이를 그대로 저장하지 않고 0,0으로 최대한 당겨서 저장해야 한다.
빈칸과 블록이 위치한 좌표가 다 다르기 때문에 0,0으로 당겨 저장한 뒤 정렬을 통해 일치시키기 위함이다.
즉, 빈칸과 블록을 정규화하는 것이다.
이때, 각 좌표의 x, y의 최솟값을 기억하여 모든 좌표에서 빼는 방법으로 간단하게 할 수 있다.
이제 회전만 구현하면 된다.
5번 블록을 예로 들면, {0, 0}, {1, 0}으로 저장되어 있을 것이다.
이를 시계방향으로 90도 회전시킨다면 {0, 4}, {0, 5}가 된다.
이를 공식으로 표현하면 다음과 같다.
i = j;
j = n-1-i;하지만 회전을 하고도 0,0으로 최대한 당겨 정규화하는 것을 잊어서는 안 된다.
최종적으로 90도를 회전하면 {0, 0}, {0, 1}이 된다.
나머지 회전은 간단하다.
90도 회전시킨 좌표들을 또다시 회전시키면 되기 때문이다.
이제 모든 빈칸과 모든 블록을 하나하나 비교하면 된다.
이때, 빈칸과 블록의 크기가 다른 것은 절대 정답이 될 수 없다.
문제의 조건을 보면 빈칸을 남기고 블록을 채울 수 없다고 되어있기 때문이다.
전체 코드
#include <string>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
using namespace std;
vector<int> dy = {0, 1, 0, -1};
vector<int> dx = {1, 0, -1, 0};
bool cmp(vector<int>& a, vector<int>& b)
{
if(a[0] == b[0]) return a[1] < b[1];
return a[0] < b[0];
}
vector<vector<int>> Rotate(vector<vector<int>>& origin, int n)
{
int minY = n;
int minX = n;
vector<vector<int>> result;
for(auto block : origin)
{
minY = min(minY, block[1]);
minX = min(minX, n-1-block[0]);
result.push_back({block[1], n-1-block[0]});
}
for(int i = 0; i < result.size(); i++)
{
result[i][0] -= minY;
result[i][1] -= minX;
}
sort(result.begin(), result.end(), cmp);
return result;
}
vector<vector<int>> Bfs(vector<vector<int>>& board, vector<vector<bool>>& visited, int y, int x, int num)
{
vector<vector<int>> result;
queue<pair<int,int>> q;
q.push({y, x});
visited[y][x] = true;
result.push_back({y, x});
int minY = board.size();
int minX = board.size();
while(!q.empty())
{
int y = q.front().first;
int x = q.front().second;
q.pop();
minY = min(minY, y);
minX = min(minX, x);
for(int i = 0; i < 4; i++)
{
int new_y = y + dy[i];
int new_x = x + dx[i];
if(new_y < 0 || new_y >= board.size() || new_x < 0 || new_x >= board.size()) continue;
if(visited[new_y][new_x]) continue;
if(board[new_y][new_x] != num) continue;
result.push_back({new_y, new_x});
q.push({new_y, new_x});
visited[new_y][new_x] = true;
}
}
for(int i = 0; i < result.size(); i++)
{
result[i][0] -= minY;
result[i][1] -= minX;
}
sort(result.begin(), result.end(), cmp);
return result;
}
pair<bool, int> Match(vector<vector<int>>& blank, vector<vector<int>>& block, int n)
{
if(blank.size() != block.size()) return {false, 0};
vector<vector<int>> temp = block;
for(int r = 0; r < 4; r++)
{
bool flag = true;
if(r != 0)
{
temp = Rotate(temp, n);
}
for(int i = 0; i < blank.size(); i++)
{
if(blank[i][0] != temp[i][0] || blank[i][1] != temp[i][1])
{
flag = false;
break;
}
}
if(flag)
{
return {true, block.size()};
}
}
return {false, 0};
}
int fillBlank(vector<vector<vector<int>>>& blanks, vector<vector<vector<int>>>& blocks, int n)
{
int result = 0;
vector<bool> usedBlck(blocks.size(), false);
for(int i = 0; i < blanks.size(); i++)
{
for(int j = 0; j < blocks.size(); j++)
{
if(usedBlck[j]) continue;
auto [bMatch, cnt] = Match(blanks[i], blocks[j], n);
if(bMatch)
{
usedBlck[j] = true;
result += cnt;
break;
}
}
}
return result;
}
int solution(vector<vector<int>> game_board, vector<vector<int>> table) {
int answer = -1;
vector<vector<vector<int>>> blanks;
vector<vector<vector<int>>> blocks;
vector<vector<bool>> blankVisited(game_board.size(), vector<bool>(game_board.size(), false));
vector<vector<bool>> blockVisited(game_board.size(), vector<bool>(game_board.size(), false));
for(int i = 0; i < game_board.size(); i++)
{
for(int j = 0; j < game_board.size(); j++)
{
if(game_board[i][j] == 0 && !blankVisited[i][j])
{
auto blank = Bfs(game_board, blankVisited, i, j, 0);
blanks.push_back(blank);
}
if(table[i][j] == 1 && !blockVisited[i][j])
{
auto block = Bfs(table, blockVisited, i, j, 1);
blocks.push_back(block);
}
}
}
answer = fillBlank(blanks, blocks, table.size());
return answer;
}
