다익스트라 알고리즘(Dijkstra's algorithm)

다익스트라 알고리즘(Dijkstra's algorithm)

다익스트라 알고리즘(Dijkstra's algorithm)은 벨만-포드 알고리즘처럼 특정한 노드에서 시작하여 그래프의 모든 노드로 가는 최단 경로를 구하는 알고리즘이다. 다익스트라는 벨만-포드 알고리즘에 비해 좀 더 효율적이기 때문에 그래프가 큰 경우에도 사용할 수 있다는 장점이 있다.
하지만, 이 알고리즘은 음수인 가중치를 가진 간선이 있는 경우에는 사용할 수 없다는 단점이 있다. 

다익스트라 알고리즘도 벨만-포드 알고리즘처럼 각 노드까지의 거리를 저장하고 탐색 과정에서 값을 줄여나간다. 
각 단계에서는 아직 처리하지 않는 노드 중 거리가 가장 작은 노드를 찾고, 그 노드에서 시작하는 모든 간선을 쭉 살펴보며 노드까지의 거리를 줄일 수 있다면 줄인다. 

1. 초기 상태(4번 노드 시작)	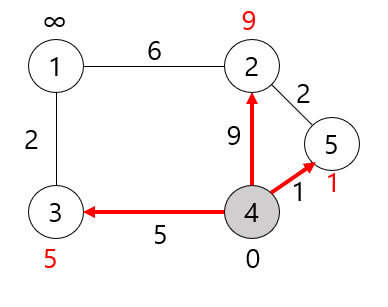2. 시작 노드에서 탐색할 수 있는 노드 탐색
3. 방문할 수 있는 노드중 가장 가까운 노드 선택	4. 방문할 수 있는 노드중 가장 가까운 노드 선택
5. 거리를 줄일 수 있으면 줄인다	6. 모든 노드를 처리하면 종료

각 노드를 방문할 때마다 그 노드에서 시작하는 간선을 이용하여 이웃한 노드까지의 거리를 줄여나간다. 
시작 노드에서 최단거리의 노드를 매 라운드마다 선택하며, 선택하여 처리한 노드까지의 거리는 변하지 않는다.

 

구현

다익스트라 알고리즘을 효율적으로 구현하기 위해서는 아직 처리하지 않은 노드 중거리가 최소인 노드를 효율적으로 찾을 수 있어야 한다. 이 과정에서 사용할 수 있는 적절한 자료 구조로는 아직 처리하지 않은 노드를 거리를 기준으로 저장하는 우선순위 큐가 있다.

그래프는 인접 리스트의 형태로 저장된다. 그리고 우선순위 큐를 사용한다. 우선순위 큐에는 (d, x)의 형태로 값을 저장하는데, 이는 노드 x까지의 거리가 d임을 의미한다. distance [] 배열은 각 노드까지의 거리가 담긴 배열이며, processed [] 배열은 노드를 처리했는지를 저장하는 배열이다.

Pair class를 Comparable interface를 구현하게 하고, 가중치를 기준으로 우선순위를 설정한다.
(낮은 숫자가 우선 순위이다.)

public class Pair implements Comparable<Pair>{
	int a;
	int b;
	public Pair(Integer a, Integer b) {
		this.a = a;
		this.b = b;
	}
	public int first() {
		return a;
	}
	public int second() {
		return b;
	}
	public int getA() {
		return a;
	}
	public void setA(int a) {
		this.a = a;
	}
	public int getB() {
		return b;
	}
	public void setB(int b) {
		this.b = b;
	}
	@Override
	public int compareTo(Pair o) {
		return o.getA() - getA();
	}
	
}

 

즉, 가중치가 낮은(거리가 가까운) 노드를 우선적으로 탐색하고, 거리를 줄여 나간다.

다음은 Java로 작성한 코드이다. 

import java.util.ArrayList;
import java.util.PriorityQueue;

import util.Pair;

public class Dijkstra {

	public static void main(String[] args) {
		//그래프
		ArrayList<ArrayList<util.Pair>> adj = new ArrayList<ArrayList<util.Pair>>();

		for(int i = 0 ; i < 5 ; i++) {
			adj.add(new ArrayList<util.Pair>());
		}
		
		adj.get(0).add(new Pair(1, 6));
		adj.get(0).add(new Pair(2, 2));
		adj.get(1).add(new Pair(0, 6));
		adj.get(1).add(new Pair(3, 9));
		adj.get(1).add(new Pair(4, 2));
		adj.get(2).add(new Pair(0, 2));
		adj.get(2).add(new Pair(3, 5));
		adj.get(3).add(new Pair(1, 9));
		adj.get(3).add(new Pair(2, 5));
		adj.get(3).add(new Pair(4, 1));
		adj.get(4).add(new Pair(1, 2));
		adj.get(4).add(new Pair(3, 1));

		//우선 순위 큐
		PriorityQueue<util.Pair> q= new PriorityQueue<util.Pair>();

		//거리 저장 배열
		int distance[] = new int[5];
		
		//처리 여부 저장
		boolean processed[] = new boolean[5];
		
		
		//거리 무한대 설정
		for( int i = 0 ; i < 5 ; i++ ) {
			distance[i] = (int)Double.POSITIVE_INFINITY;
		}
		
		//4번노드 시작, 시작 거리 0으로 설정
		distance[3] = 0;
		
		q.add(new Pair(0, 3));
		
		//계산
		while(!q.isEmpty()) {
			int a = q.peek().second();
			q.poll();
			
			if(processed[a]) {
				continue;
			}
			
			processed[a] = true;
			for(Pair u : adj.get(a)) {
				int b = u.first();
				int w = u.second();
				
				if(distance[a] + w < distance[b]) {
					distance[b] = distance[a] + w;
					q.add(new Pair(distance[b], b));
				}
			}
		}
		
		//출력
		for(int i = 0 ; i < 5 ; i++ ) {
			System.out.println(i+"노드 거리: "+distance[i]);
		}
	}

}

 우선순위 큐에 가중치가 낮은 순으로 정렬되어 있고, 가까운 순으로 뽑아와 탐색을 진행한다. 이미 처리한 노드이면 건너뛴다. 거리를 줄일 수 있다면, 줄여나간다.