문제 설명
n명의 사람이 일렬로 줄을 서고 있습니다. n명의 사람들에게는 각각 1번부터 n번까지 번호가 매겨져 있습니다. n명이 사람을 줄을 서는 방법은 여러가지 방법이 있습니다. 예를 들어서 3명의 사람이 있다면 다음과 같이 6개의 방법이 있습니다.
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
사람의 수 n과, 자연수 k가 주어질 때, 사람을 나열 하는 방법을 사전 순으로 나열 했을 때, k번째 방법을 return하는 solution 함수를 완성해주세요.
https://school.programmers.co.kr/learn/courses/30/lessons/12936#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
제한 사항
- n은 20이하의 자연수 입니다.
- k는 n! 이하의 자연수 입니다.
풀이
순열을 생성하는 문제이다.
하지만, k번째 순열을 찾아내야 하는 조건이 붙는다.
처음에는 모든 순열을 만들어 저장한 뒤 k번째 순열을 찾았다.
정확도 테스트는 모두 성공했지만 시간 초과가 발생했다.
두 번째 방법으로는 k번째 순열을 만드는 순간 종료하려 했다.
하지만, 여기서도 시간초과가 발생했다.
따라서, 다른 접근법이 필요했다.
발견한 규칙은 /, %를 이용하여 계산할 수 있다는 것이다.
우선 제일 앞자리만 놓고 생각을 해보자.
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
제일 앞자리는 그 뒷자리들의 경우의 수에 따라 결정된다.
예를 들어 3자리를 만들 때, XOO를 만들어야 한다고 가정해 보자.
1XX가 될 수 있는 개수는 [1, 2, 3], [1, 3, 2] 2개이다.
즉, 2XX가 되는 경우는 1XX의 경우의 수 다음이다.
이를 식으로 정리하면 다음과 같이 일반화할 수 있다.
i번째 수 = k / factorial[n-i] + 1
이때, 수열은 중복을 허용하지 않기 때문에 i번째 수는 결과 값이 아닌 남아있는 수 중 앞에서부터 세어 골라야 한다.
그리고 뒤의 자리들을 결정하기 위해서는 나머지를 통해 구해내야 한다.
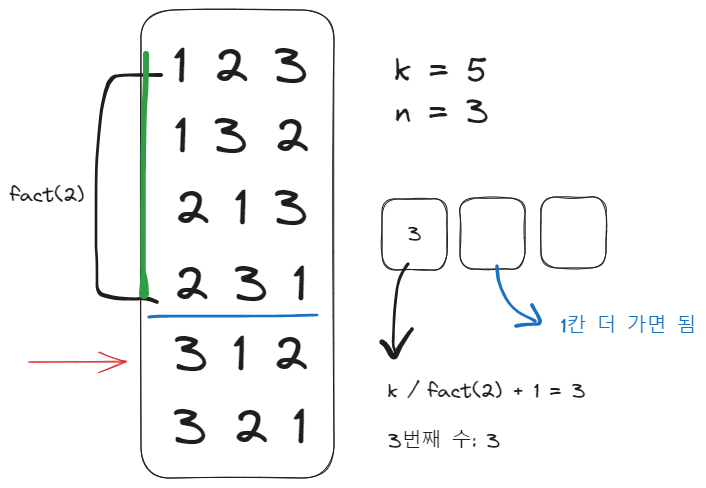
즉, k % fact[n-i]가 남은 수가 된다.
하지만 여기서 주의해야 할 부분이 있다.
만약 k가 fact[n-i]로 나누어 떨어진다면 앞자리를 하나 내리고 나머지 수를 fact[n-i]로 해주어야 한다.
뺄셈의 자릿수 변경과 같은 원리이다.
이러한 식으로 마지막 한 자리를 남기고 진행한 뒤 남은 한 자리는 아직 넣지 않은 수를 넣어주면 된다.
전체 코드
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int findK(int k, int n, vector<bool>& checked)
{
for(int i = 1; i <= n; i++)
{
if(checked[i]) continue;
k--;
if(k==0)
{
checked[i] = true;
return i;
}
}
}
vector<int> solution(int n, long long k) {
vector<int> answer;
vector<bool> checked(n+1, false);
vector<long long> fact;
fact.push_back(0);
fact.push_back(1);
for(int i = 2; i <= n; i++)
{
fact.push_back(fact[i-1] * i);
}
for(int i = n-1; i > 0; i--)
{
int temp = (k / fact[i]) + 1;
if((k % fact[i]) == 0)
{
temp--;
k = fact[i];
}
else
{
k %= fact[i];
}
answer.push_back(findK(temp, n, checked));
}
answer.push_back(findK(1, n, checked));
return answer;
}
문제 설명
n명의 사람이 일렬로 줄을 서고 있습니다. n명의 사람들에게는 각각 1번부터 n번까지 번호가 매겨져 있습니다. n명이 사람을 줄을 서는 방법은 여러가지 방법이 있습니다. 예를 들어서 3명의 사람이 있다면 다음과 같이 6개의 방법이 있습니다.
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
사람의 수 n과, 자연수 k가 주어질 때, 사람을 나열 하는 방법을 사전 순으로 나열 했을 때, k번째 방법을 return하는 solution 함수를 완성해주세요.
https://school.programmers.co.kr/learn/courses/30/lessons/12936#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
제한 사항
- n은 20이하의 자연수 입니다.
- k는 n! 이하의 자연수 입니다.
풀이
순열을 생성하는 문제이다.
하지만, k번째 순열을 찾아내야 하는 조건이 붙는다.
처음에는 모든 순열을 만들어 저장한 뒤 k번째 순열을 찾았다.
정확도 테스트는 모두 성공했지만 시간 초과가 발생했다.
두 번째 방법으로는 k번째 순열을 만드는 순간 종료하려 했다.
하지만, 여기서도 시간초과가 발생했다.
따라서, 다른 접근법이 필요했다.
발견한 규칙은 /, %를 이용하여 계산할 수 있다는 것이다.
우선 제일 앞자리만 놓고 생각을 해보자.
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
제일 앞자리는 그 뒷자리들의 경우의 수에 따라 결정된다.
예를 들어 3자리를 만들 때, XOO를 만들어야 한다고 가정해 보자.
1XX가 될 수 있는 개수는 [1, 2, 3], [1, 3, 2] 2개이다.
즉, 2XX가 되는 경우는 1XX의 경우의 수 다음이다.
이를 식으로 정리하면 다음과 같이 일반화할 수 있다.
i번째 수 = k / factorial[n-i] + 1
이때, 수열은 중복을 허용하지 않기 때문에 i번째 수는 결과 값이 아닌 남아있는 수 중 앞에서부터 세어 골라야 한다.
그리고 뒤의 자리들을 결정하기 위해서는 나머지를 통해 구해내야 한다.

즉, k % fact[n-i]가 남은 수가 된다.
하지만 여기서 주의해야 할 부분이 있다.
만약 k가 fact[n-i]로 나누어 떨어진다면 앞자리를 하나 내리고 나머지 수를 fact[n-i]로 해주어야 한다.
뺄셈의 자릿수 변경과 같은 원리이다.
이러한 식으로 마지막 한 자리를 남기고 진행한 뒤 남은 한 자리는 아직 넣지 않은 수를 넣어주면 된다.
전체 코드
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int findK(int k, int n, vector<bool>& checked)
{
for(int i = 1; i <= n; i++)
{
if(checked[i]) continue;
k--;
if(k==0)
{
checked[i] = true;
return i;
}
}
}
vector<int> solution(int n, long long k) {
vector<int> answer;
vector<bool> checked(n+1, false);
vector<long long> fact;
fact.push_back(0);
fact.push_back(1);
for(int i = 2; i <= n; i++)
{
fact.push_back(fact[i-1] * i);
}
for(int i = n-1; i > 0; i--)
{
int temp = (k / fact[i]) + 1;
if((k % fact[i]) == 0)
{
temp--;
k = fact[i];
}
else
{
k %= fact[i];
}
answer.push_back(findK(temp, n, checked));
}
answer.push_back(findK(1, n, checked));
return answer;
}