백준 5827 - What's Up With Gravity

문제 설명

Captain Bovidian is on an adventure to rescue her crew member, Doctor Beefalo. Like all great adventures, this story plays out in a two dimensional N by M grid (1 <= N, M <= 500), representing a side view of the captain's world. Some grid cells are empty while others are blocked and cannot be traversed.

Unfortunately, Captain Bovidian cannot jump. She must obey the following rules of physics while traversing her world.

1) If there is no cell directly underneath Captain Bovidian (that is, if she is at the edge of the grid), then she flies out into space and fails her mission. 2) If the cell directly underneath Captain Bovidian is empty, then she falls into that cell. 3) Otherwise: a) Captain Bovidian may move left or right if the corresponding cell exists and is empty. b) Or, Captain Bovidian may flip the direction of gravity.

When Captain Bovidian changes the direction of gravity, the cell that's 'underneath' her (as mentioned in rules 1 and 2) toggles between the cell with one higher row index and the cell with one lower row index (the first row in the input has index 1, and the last row has index N). Initially, the cells with one higher row index are underneath Captain Bovidian.

Doctor Beefalo is lost somewhere in this world. Help Captain Bovidian arrive at her cell using the least number of gravity flips as possible. If it is impossible to reach Doctor Beefalo, please output -1.

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, C에서 D로 가는 최소 비용을 구하는 것이다.

이때, 적용되는 규칙은 다음과 같다.

• C는 왼쪽, 오른쪽, 현재 중력의 반대 방향으로 이동할 수 있다.
  • 왼쪽, 오른쪽으로 이동하는 것은 비용이 들지 않는다.
  • 중력의 방향을 바꿔 이동하는 경우 비용이 1 발생한다.
• C는 항상 현재 중력 방향으로 떨어진다.
  • 중력에 의해 Space밖으로 이동한 경우 미션 실패이다.
  • 중력에 의해 이동하다 벽(#)을 만나면 멈춘다.

 

결국, 문제를 풀기 위해서는 C에서 D로 가는 경로를 구해야 한다.

즉, BFS나 DFS를 이용하여 문제를 풀어야 한다.

해당 문제는 이동 방향에 따라 결과가 달라지므로 DFS를 사용하면 풀 수 있다.

하지만, 0-1 BFS를 사용하면 효율적으로 풀 수 있다.

 

0-1 BFS는 기존 BFS를 변형하여 최단 경로를 찾는 알고리즘이다.

0-1이란 이름이 붙은 이유는 가중치가 0 혹은 1인 그래프에 사용가능하기 때문이다.

동작 원리는 간단하다.

기존 BFS는 Queue를 이용하여 경로를 찾는다.

0-1 BFS는 Deque을 이용하여 경로를 찾는다.

Deque의 가장 앞에 있는 요소부터 순차적으로 탐색을 진행한다.

따라서, 가중치가 낮은 0은 Deque의 앞에 가중치가 높은 1은 Deque의 뒤에 넣으면 탐색한다.

이렇게 되면 Deque의 요소는 항상 오름차순으로 정렬이 된다.

 

0-1 BFS를 이번 문제에 적용하면 다음과 같다.

비용이 발생하는 중력을 바꾸는 경우에는 Deque의 뒤에 추가한다.

그렇지 않은 왼쪽, 오른쪽의 이동은 Deque의 앞에 추가한다.

 

예를 들어 보자.

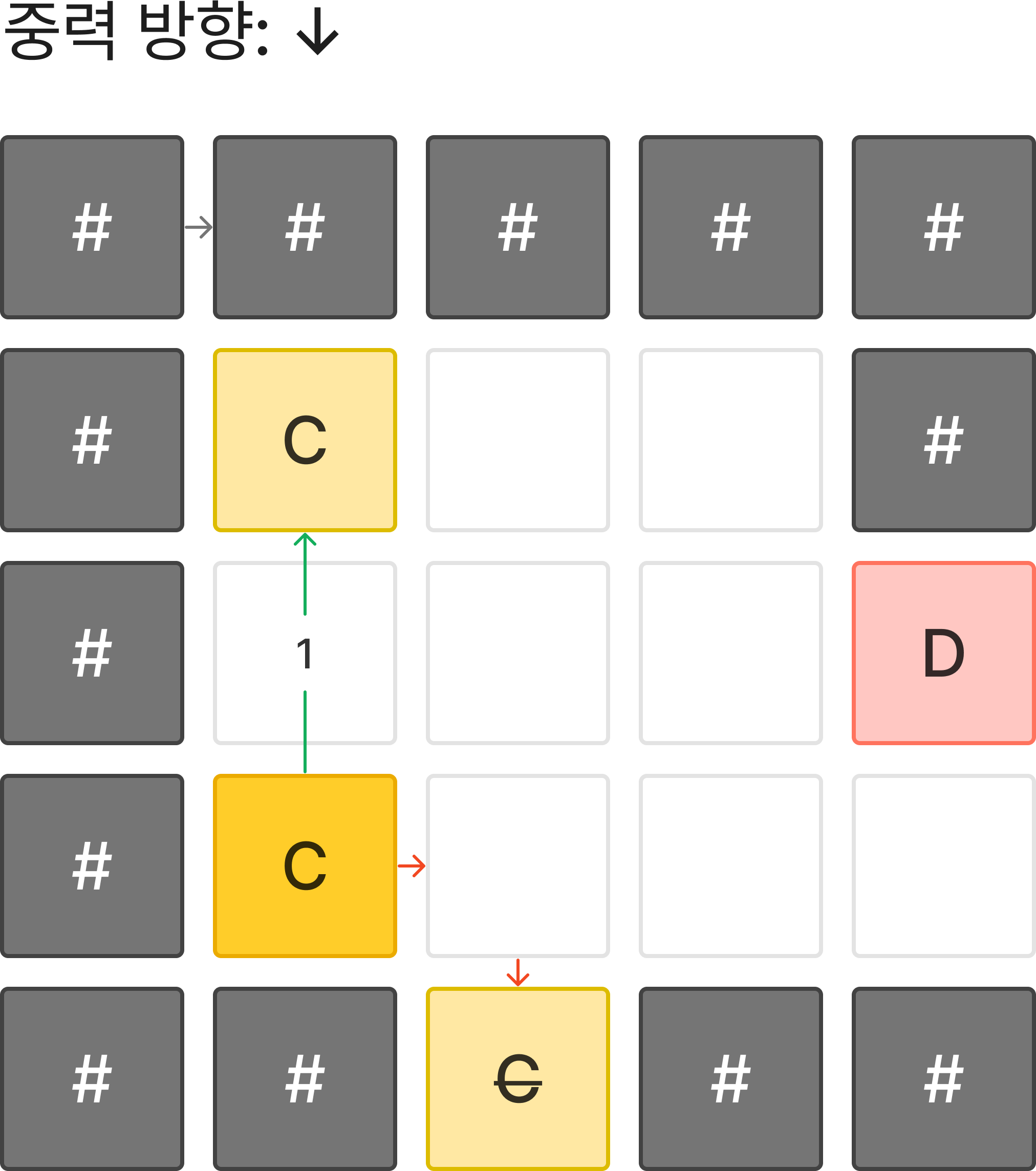
C가 이동할 수 있는 경우는 다음과 같다.

• 왼쪽
  • 벽(#)에 막혀 이동할 수 없다.
• 오른쪽
  • 이동이 가능하나, 중력에 의해 떨어져 Space 밖으로 이동한다.
• 중력 변경
  • 이동 가능하다.
  • 비용이 1 발생한다.

처음엔 중력을 바꿔 이동하는 경우밖에 선택지가 없다.

해당 경우에는 중력을 바꿔 비용이 발생했기 때문에 Deque의 뒤에 추가한다.

이후 과정을 살펴보자.

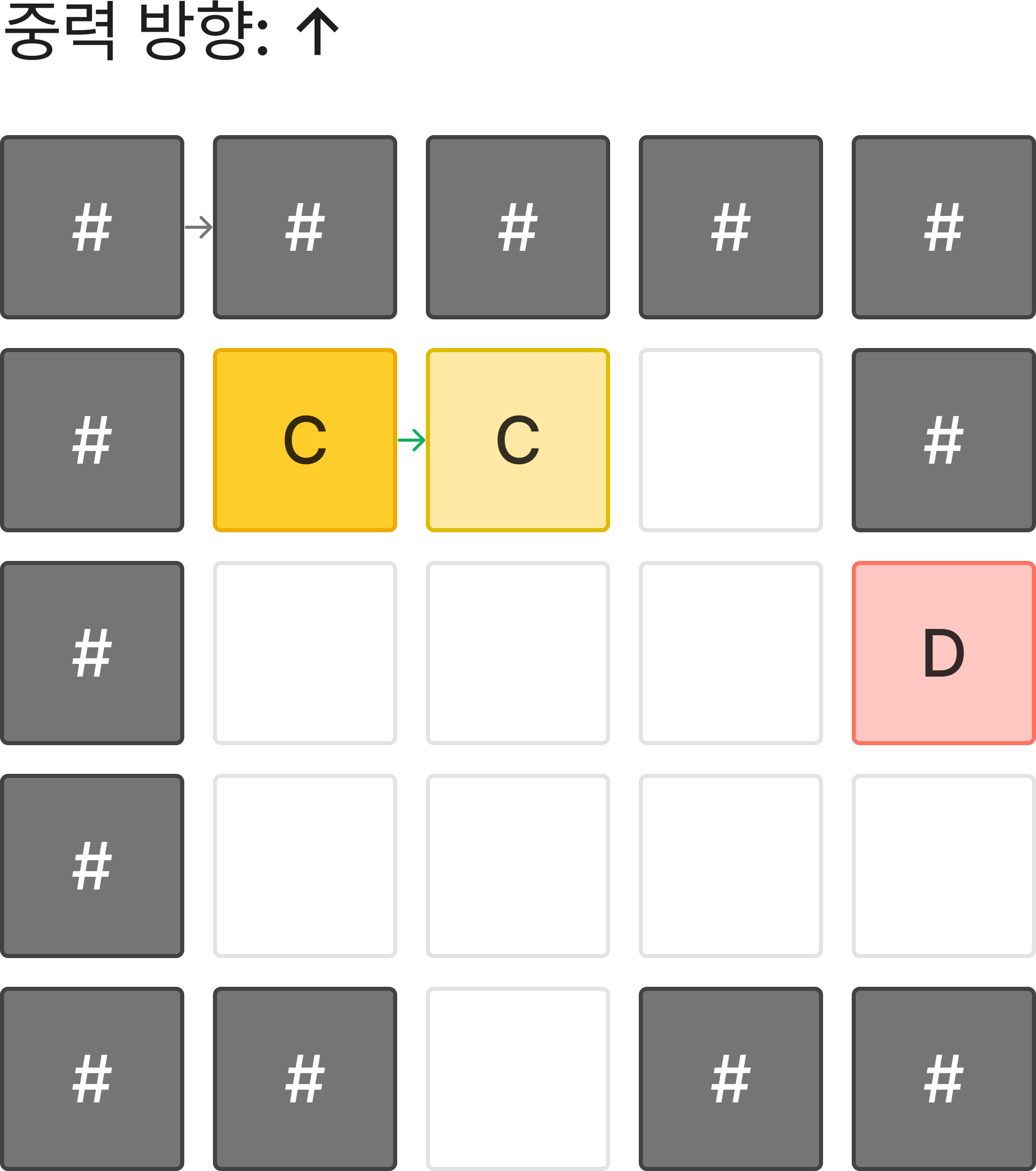
왼쪽은 역시 벽에 막혀 이동할 수 없다.

오른쪽은 이동가능하다. 비용이 발생하지 않기 때문에 Deque의 앞에 추가할 수 있다.

중력의 방향을 변경하는 것도 역시 가능하나 이미 탐색한 지역이기 때문에 굳이 추가할 필요가 없다.

 

이런 식으로 탐색을 진행하다 D를 발견하는 경우 탐색을 종료하면 된다.

만약, Deque가 비었다면 D를 찾을 수 없다는 뜻으로 -1을 출력하면 된다.

 

한 가지 주의할 점이 있다면, 왼쪽 혹은 오른쪽으로 이동한 경우 중력에 의해 떨어지기 전에 D를 발견하여도 미션 성공으로 판정한다.

또한, 중력에 의해 떨어지는 과정에서 D를 발견하여도 미션 성공이다.

 

그리고 C가 공중에 떠 있는 상태로 시작될 수 있기 때문에 처음에 중력에 의한 이동을 한 번 해주어야 한다. 

---

 

 

 

 

 

전체 코드

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>

using namespace std;

int N, M;

vector<int> dy = { 1, -1, 0, 0 };
vector<int> dx = { 0, 0, 1, -1 };

enum Move
{
    DOWN,
    UP,
    RIGHT,
    LEFT
};

bool IsMovable(vector<vector<char>>& Space, int dir, pair<int,int>& CaptainPos)
{
    auto [newY, newX] = CaptainPos;

    while (true)
    {
        newY += dy[dir];
        newX += dx[dir];

        if (newY < 0 || newY >= N) return false;
        if (Space[newY][newX] == 'D')
        {
            CaptainPos = { newY, newX };
            return true;
        }
        if (Space[newY][newX] == '#') break;
    }

    newY -= dy[dir];
    newX -= dx[dir];

    CaptainPos = { newY, newX };

    return true;
}

bool IsInner(int y, int x)
{
    return (y >= 0 && y < N && x >= 0 && x < M);
}

int BFS(vector<vector<char>>& Space, pair<int, int>& CaptainPos)
{
    //switch, {y, x}
    deque<pair<int, pair<int,int>>> dq;
    vector<vector<bool>> visited(N, vector<bool>(M, false));

    dq.push_back({ 0, CaptainPos });

    //cost: 홀수 -> UP, 짝수 -> DOWN
    while (!dq.empty())
    {
        auto [cost, pos] = dq.front();
        dq.pop_front();

        if (visited[pos.first][pos.second]) continue;
        visited[pos.first][pos.second] = true;
        int DIR = cost % 2;

        //LEFT
        {
            int newY = pos.first + dy[LEFT];
            int newX = pos.second + dx[LEFT];

            //cost = 0 : front
            if (IsInner(newY, newX))
            {
                if (Space[newY][newX] == 'D') return cost;

                pair<int, int> newCaptainPos = { newY, newX };
                if (Space[newY][newX] == '.' && IsMovable(Space, DIR, newCaptainPos))
                {
                    if (Space[newCaptainPos.first][newCaptainPos.second] == 'D') return cost;
                    dq.push_front({ cost, newCaptainPos });
                }
            }
        }

        //RIGHT
        {
            int newY = pos.first + dy[RIGHT];
            int newX = pos.second + dx[RIGHT];

            //cost = 0 : front
            if (IsInner(newY, newX))
            {
                if (Space[newY][newX] == 'D') return cost;

                pair<int, int> newCaptainPos = { newY, newX };
                if (Space[newY][newX] == '.' && IsMovable(Space, DIR, newCaptainPos))
                {
                    if (Space[newCaptainPos.first][newCaptainPos.second] == 'D') return cost;
                    dq.push_front({ cost, newCaptainPos });
                }
            }
        }


        //DIR
        {
            int newDir = (DIR + 1) % 2;
            pair<int, int> newCaptainPos = { pos.first, pos.second };

            if (IsMovable(Space, newDir, newCaptainPos))
            {
                if (Space[newCaptainPos.first][newCaptainPos.second] == 'D') return cost+1;
                dq.push_back({ cost + 1, newCaptainPos });
            }
        }
    }

    return -1;
}

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M;

    vector<vector<char>> Space(N, vector<char>(M, '.'));
    pair<int, int> CaptainPos;
    pair<int, int> DoctorPos;

    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < M; j++)
        {
            cin >> Space[i][j];
            if (Space[i][j] == 'C') CaptainPos = { i,j };
            else if (Space[i][j] == 'D') DoctorPos = { i,j };
        }
    }

    if (!IsMovable(Space, DOWN, CaptainPos))
    {
        cout << -1;
        return 0;
    }

    cout << BFS(Space, CaptainPos);

	return 0;
}

---