문제 설명
1번부터 N번까지의 학생들은 각각 블록들을 가지고 있다. 학생마다 최대 M개의 블록을 가지고 있을 수 있으며, 한 명의 학생이 가지고 있는 모든 블록들의 높이는 서로 다르다. 이 때 1번부터 N번까지의 학생들이 가진 블록을 차례대로 사용하여 바닥에서부터 쌓아올려 하나의 탑을 만들고자 한다.
단, 어떤 학생의 블록은 사용하지 않아도 되며 한 학생당 최대 1개의 블록만을 사용할 수 있다.
1번부터 N번까지의 학생들이 가지고 있는 블록들에 대한 정보가 주어졌을 때, 높이가 정확히 H인 탑을 만들 수 있는 경우의 수를 계산하는 프로그램을 작성하시오.
예를 들어 N=3, M=3, H=5일 때, 각 학생마다 가지고 있는 블록들의 높이가 다음과 같다고 가정하자.
- 1번 학생: 2, 3, 5
- 2번 학생: 3, 5
- 3번 학생: 1, 2, 3
이 때, 탑의 높이가 정확히 5가 되도록 블록을 쌓는 경우로는 다음의 6가지가 존재한다. (블록을 사용하지 않는 경우는 X로 표시하였다.)
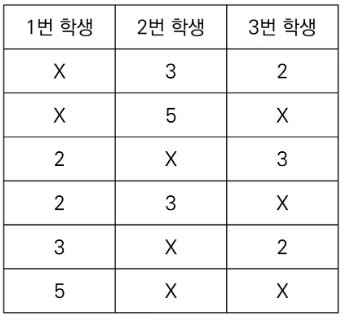
제한 사항


풀이
문제를 요약하면, N명의 학생이 하나의 블록을 쌓아 H를 만드는 것이다.
즉, 각 학생이 하나의 블록을 선택하여 목표를 만드는 것이다.
이때, 블록을 쌓지 않아도 된다.
즉, 선택지가 하나 늘어난다는 뜻이다.
이 문제는 DP를 이용하면 간단하게 풀 수 있다.
N번째 학생은 N-1번째 학생이 만들어 놓은 높이에 자신의 블록을 쌓을 수 있다.
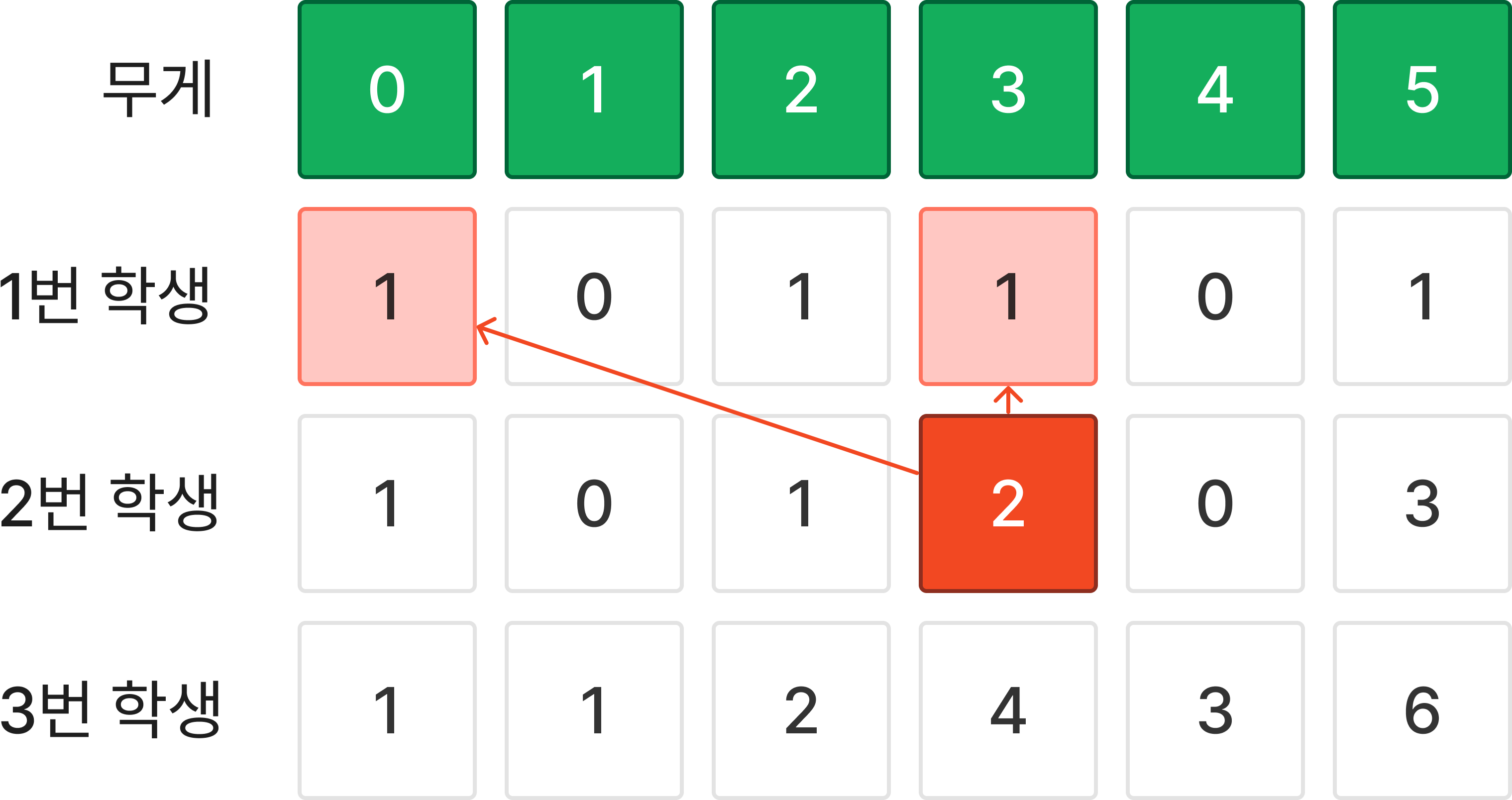
여기서 주의할 점은 N번째 학생이 블록을 쌓지 않을 수 있다는 것이다.
즉, 0의 높이를 쌓을 수 있다는 뜻이다.
따라서, 블록을 추가할 때 높이가 0인 블록을 추가하여 해당 경우를 처리할 수 있다.
for (int i = 1; i < N; i++)
{
for (int j = 0; j <= H; j++)
{
for (int k = 0; k < Blocks[i].size(); k++)
{
int prev = j - Blocks[i][k];
if (prev < 0) continue;
DP[i][j] = (DP[i][j] + DP[i - 1][prev]) % DIV;
}
}
}
이 문제에서 가장 중요했던것은 DP를 푸는 게 아니다.
입력을 처리하는 것이 가장 중요했다.
입력을 제대로 처리하지 않아 계속 문제를 틀렸었다.
입력을 받는 과정이 까다로웠던 이유는 학생마다 블록의 개수가 달랐다.
개수에 대한 정보없이 주어진 문자열을 통해 알아내야 했다.
처음 문제를 풀었을 때는 띄어쓰기와 개행 문자로 구분하였다.
예제는 문제없이 해결했지만, 제출하면 계속 틀렸다.
블록의 높이가 2자리수 이상이라는 점을 간과했다.
따라서, 다음과 같이 처리해야 한다.
cin >> N >> M >> H;
cin.ignore();
for (int i = 0; i < N; i++)
{
string str;
getline(cin, str);
stringstream sstr(str);
int num;
Blocks[i].push_back(0);
while (sstr >> num) Blocks[i].push_back(num);
}
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M, H;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M >> H;
vector<vector<int>> Blocks(N);
vector<vector<int>> DP(N, vector<int>(H+1, 0));
const int DIV = 10'007;
cin.ignore();
for (int i = 0; i < N; i++)
{
string str;
getline(cin, str);
stringstream sstr(str);
int num;
Blocks[i].push_back(0);
while (sstr >> num) Blocks[i].push_back(num);
}
for (int i = 0; i < Blocks[0].size(); i++) DP[0][Blocks[0][i]] = 1;
for (int i = 1; i < N; i++)
{
for (int j = 0; j <= H; j++)
{
for (int k = 0; k < Blocks[i].size(); k++)
{
int prev = j - Blocks[i][k];
if (prev < 0) continue;
DP[i][j] = (DP[i][j] + DP[i - 1][prev]) % DIV;
}
}
}
for (auto row : DP)
{
for (auto c : row)
{
cout << c << " ";
}
cout << "\n";
}
cout << DP[N-1][H];
return 0;
}
문제 설명
1번부터 N번까지의 학생들은 각각 블록들을 가지고 있다. 학생마다 최대 M개의 블록을 가지고 있을 수 있으며, 한 명의 학생이 가지고 있는 모든 블록들의 높이는 서로 다르다. 이 때 1번부터 N번까지의 학생들이 가진 블록을 차례대로 사용하여 바닥에서부터 쌓아올려 하나의 탑을 만들고자 한다.
단, 어떤 학생의 블록은 사용하지 않아도 되며 한 학생당 최대 1개의 블록만을 사용할 수 있다.
1번부터 N번까지의 학생들이 가지고 있는 블록들에 대한 정보가 주어졌을 때, 높이가 정확히 H인 탑을 만들 수 있는 경우의 수를 계산하는 프로그램을 작성하시오.
예를 들어 N=3, M=3, H=5일 때, 각 학생마다 가지고 있는 블록들의 높이가 다음과 같다고 가정하자.
- 1번 학생: 2, 3, 5
- 2번 학생: 3, 5
- 3번 학생: 1, 2, 3
이 때, 탑의 높이가 정확히 5가 되도록 블록을 쌓는 경우로는 다음의 6가지가 존재한다. (블록을 사용하지 않는 경우는 X로 표시하였다.)

제한 사항


풀이
문제를 요약하면, N명의 학생이 하나의 블록을 쌓아 H를 만드는 것이다.
즉, 각 학생이 하나의 블록을 선택하여 목표를 만드는 것이다.
이때, 블록을 쌓지 않아도 된다.
즉, 선택지가 하나 늘어난다는 뜻이다.
이 문제는 DP를 이용하면 간단하게 풀 수 있다.
N번째 학생은 N-1번째 학생이 만들어 놓은 높이에 자신의 블록을 쌓을 수 있다.

여기서 주의할 점은 N번째 학생이 블록을 쌓지 않을 수 있다는 것이다.
즉, 0의 높이를 쌓을 수 있다는 뜻이다.
따라서, 블록을 추가할 때 높이가 0인 블록을 추가하여 해당 경우를 처리할 수 있다.
for (int i = 1; i < N; i++)
{
for (int j = 0; j <= H; j++)
{
for (int k = 0; k < Blocks[i].size(); k++)
{
int prev = j - Blocks[i][k];
if (prev < 0) continue;
DP[i][j] = (DP[i][j] + DP[i - 1][prev]) % DIV;
}
}
}
이 문제에서 가장 중요했던것은 DP를 푸는 게 아니다.
입력을 처리하는 것이 가장 중요했다.
입력을 제대로 처리하지 않아 계속 문제를 틀렸었다.
입력을 받는 과정이 까다로웠던 이유는 학생마다 블록의 개수가 달랐다.
개수에 대한 정보없이 주어진 문자열을 통해 알아내야 했다.
처음 문제를 풀었을 때는 띄어쓰기와 개행 문자로 구분하였다.
예제는 문제없이 해결했지만, 제출하면 계속 틀렸다.
블록의 높이가 2자리수 이상이라는 점을 간과했다.
따라서, 다음과 같이 처리해야 한다.
cin >> N >> M >> H;
cin.ignore();
for (int i = 0; i < N; i++)
{
string str;
getline(cin, str);
stringstream sstr(str);
int num;
Blocks[i].push_back(0);
while (sstr >> num) Blocks[i].push_back(num);
}
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M, H;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M >> H;
vector<vector<int>> Blocks(N);
vector<vector<int>> DP(N, vector<int>(H+1, 0));
const int DIV = 10'007;
cin.ignore();
for (int i = 0; i < N; i++)
{
string str;
getline(cin, str);
stringstream sstr(str);
int num;
Blocks[i].push_back(0);
while (sstr >> num) Blocks[i].push_back(num);
}
for (int i = 0; i < Blocks[0].size(); i++) DP[0][Blocks[0][i]] = 1;
for (int i = 1; i < N; i++)
{
for (int j = 0; j <= H; j++)
{
for (int k = 0; k < Blocks[i].size(); k++)
{
int prev = j - Blocks[i][k];
if (prev < 0) continue;
DP[i][j] = (DP[i][j] + DP[i - 1][prev]) % DIV;
}
}
}
for (auto row : DP)
{
for (auto c : row)
{
cout << c << " ";
}
cout << "\n";
}
cout << DP[N-1][H];
return 0;
}