문제 설명
채영이는 거울을 들여다보는 것을 참 좋아한다. 그래서 집 곳곳에 거울을 설치해두고 집 안을 돌아다닐 때마다 거울을 보곤 한다.
채영이는 새 해를 맞이하여 이사를 하게 되었는데, 거울을 좋아하는 그녀의 성격 때문에 새 집에도 거울을 매달만한 위치가 여러 곳 있다. 또한 채영이네 새 집에는 문이 두 개 있는데, 채영이는 거울을 잘 설치하여 장난을 치고 싶어졌다. 즉, 한 쪽 문에서 다른 쪽 문을 볼 수 있도록 거울을 설치하고 싶어졌다.
채영이네 집에 대한 정보가 주어졌을 때, 한 쪽 문에서 다른 쪽 문을 볼 수 있도록 하기 위해 설치해야 하는 거울의 최소 개수를 구하는 프로그램을 작성하시오.
거울을 설치할 때에는 45도 기울어진 대각선 방향으로 설치해야 한다. 또한 모든 거울은 양면 거울이기 때문에 양 쪽 모두에서 반사가 일어날 수 있다. 채영이는 거울을 매우 많이 가지고 있어서 거울이 부족한 경우는 없다고 하자.
거울을 어떻게 설치해도 한 쪽 문에서 다른 쪽 문을 볼 수 없는 경우는 주어지지 않는다.
https://www.acmicpc.net/problem/2151
제한 사항

풀이
문제를 요약하면, '#'에서 '#'으로 가는 경로중 '!'이 있다면 거울을 설치하여 방향을 바꿀 수 있고 '.'이면 직진해야 한다.
이때, 거울을 최대한 적게 사용하는 경로에서 사용된 거울의 개수를 구하는 것이다.
이전에 비슷한 문제를 푼적이 있다.
백준 6087 - 레이저 통신
문제 설명크기가 1×1인 정사각형으로 나누어진 W×H 크기의 지도가 있다. 지도의 각 칸은 빈 칸이거나 벽이며, 두 칸은 'C'로 표시되어 있는 칸이다.'C'로 표시되어 있는 두 칸을 레이저로 통신하기
hvvan.tistory.com
이와 비슷하게 문제를 풀면 된다.
문제의 핵심은 deque를 사용한 0-1 BFS이다.
거울을 설치하는 것을 비용으로 정해, 거울이 설치되면 +1 그렇지 않으면 그냥 진행하는 식으로 진행한다.
문제의 요구사항은 가장 적게 거울을 사용해야 하는 것이므로 거울을 사용할 때는 deque의 뒤에 그렇지 않으면 deque의 앞에 추가한다.

#(0,3)에서 출발하여 아래칸(1,3)은 .이기 때문에 거울을 설치할 수 없다.
그렇기 때문에 deque의 앞에 추가한다.
또한, 방향을 바꿀 수 없기 때문에 직진만 한다.
이후, !인 칸(2,3)에 도착하면 왼쪽 혹은 오른쪽으로 방향을 변경할 수 있다.
하지만 오른쪽은 벽으로 막혀있기 때문에 진행할 수 없다.
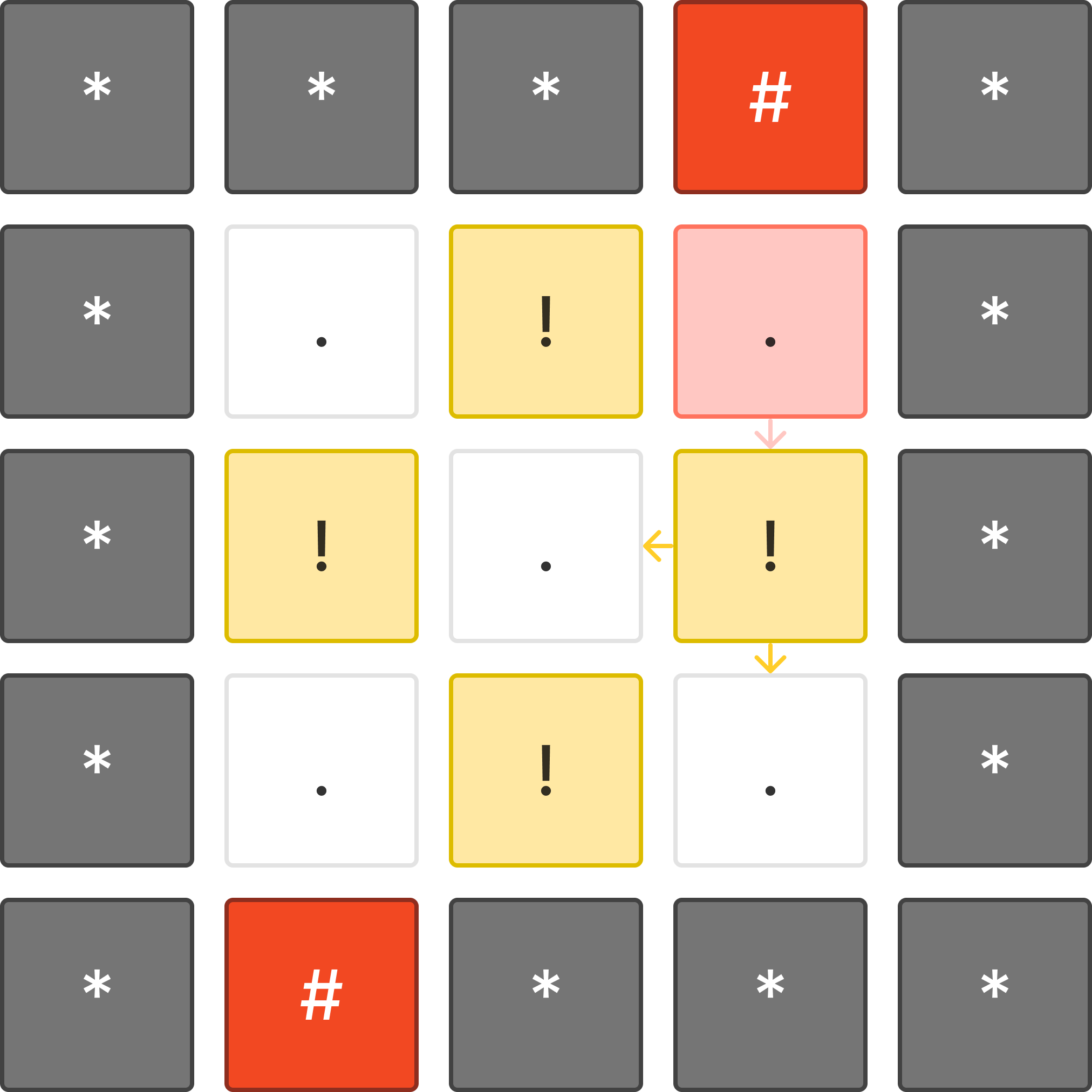
만약, 왼쪽으로 이동한다면 거울을 설치한 것이기 때문에 deque의 뒤에 추가한다.
그렇지 않고, 직진했다면 deque의 앞에 추가한다.
이런 방법으로 BFS를 진행하며 최솟값을 갱신하고 최솟값보다 현재 거울의 개수가 많다면 더 이상 진행하지 않아도 된다.
이는 0-1 BFS의 특징인데, deque는 비용으로 정렬이 되어 있다.
비용이 늘어나는 것은 뒤쪽에 추가하기 때문에 비용이 적은 분기는 앞쪽에 있을 수밖에 없다.
즉, 최솟값보다 더 큰 비용이 나온 순간 그 뒤에있는 것들은 무조건 최솟값보다 더 많다는 뜻이다.
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
long long N;
bool IsInner(int y, int x)
{
return (y >= 0 && y < N && x >= 0 && x < N);
}
int BFS(vector<vector<char>>& Room, vector<pair<int, int>>& Doors)
{
int result = INT_MAX;
auto Start = Doors[0];
auto End = Doors[1];
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
vector<int> di = { 0, -1, 1 };
//y, x, dir, mirror
deque<tuple<int, int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, 0));
for (int i = 0; i < 4; i++)
{
int newY = Start.first + dy[i];
int newX = Start.second + dx[i];
if (!IsInner(newY, newX)) continue;
if (Room[newY][newX] == '*') continue;
dq.push_back({ Start.first, Start.second, i, 0 });
}
while (!dq.empty())
{
auto [y, x, dir, mirror] = dq.front();
dq.pop_front();
if (mirror >= result) break;
int iterCnt = Room[y][x] == '!' ? 3 : 1;
for (int i = 0; i < iterCnt; i++)
{
int newDir = (dir + di[i] + 4) % 4;
int addMirror = i > 0 ? 1 : 0;
int newY = y + dy[newDir];
int newX = x + dx[newDir];
if (!IsInner(newY, newX)) continue;
if (Room[newY][newX] == '*') continue;
if (newY == End.first && newX == End.second)
{
result = min(result, mirror+ addMirror);
continue;
}
if (addMirror == 1)
{
dq.push_back({ newY, newX, newDir, mirror+addMirror });
}
else
{
dq.push_front({ newY, newX, newDir, mirror });
}
}
}
return result;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<char>> Room(N, vector<char>(N));
vector<pair<int, int>> Doors;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> Room[i][j];
if (Room[i][j] == '#')
{
Doors.push_back({ i,j });
}
}
}
cout << BFS(Room, Doors);
return 0;
}
문제 설명
채영이는 거울을 들여다보는 것을 참 좋아한다. 그래서 집 곳곳에 거울을 설치해두고 집 안을 돌아다닐 때마다 거울을 보곤 한다.
채영이는 새 해를 맞이하여 이사를 하게 되었는데, 거울을 좋아하는 그녀의 성격 때문에 새 집에도 거울을 매달만한 위치가 여러 곳 있다. 또한 채영이네 새 집에는 문이 두 개 있는데, 채영이는 거울을 잘 설치하여 장난을 치고 싶어졌다. 즉, 한 쪽 문에서 다른 쪽 문을 볼 수 있도록 거울을 설치하고 싶어졌다.
채영이네 집에 대한 정보가 주어졌을 때, 한 쪽 문에서 다른 쪽 문을 볼 수 있도록 하기 위해 설치해야 하는 거울의 최소 개수를 구하는 프로그램을 작성하시오.
거울을 설치할 때에는 45도 기울어진 대각선 방향으로 설치해야 한다. 또한 모든 거울은 양면 거울이기 때문에 양 쪽 모두에서 반사가 일어날 수 있다. 채영이는 거울을 매우 많이 가지고 있어서 거울이 부족한 경우는 없다고 하자.
거울을 어떻게 설치해도 한 쪽 문에서 다른 쪽 문을 볼 수 없는 경우는 주어지지 않는다.
https://www.acmicpc.net/problem/2151
제한 사항


풀이
문제를 요약하면, '#'에서 '#'으로 가는 경로중 '!'이 있다면 거울을 설치하여 방향을 바꿀 수 있고 '.'이면 직진해야 한다.
이때, 거울을 최대한 적게 사용하는 경로에서 사용된 거울의 개수를 구하는 것이다.
이전에 비슷한 문제를 푼적이 있다.
백준 6087 - 레이저 통신
문제 설명크기가 1×1인 정사각형으로 나누어진 W×H 크기의 지도가 있다. 지도의 각 칸은 빈 칸이거나 벽이며, 두 칸은 'C'로 표시되어 있는 칸이다.'C'로 표시되어 있는 두 칸을 레이저로 통신하기
hvvan.tistory.com
이와 비슷하게 문제를 풀면 된다.
문제의 핵심은 deque를 사용한 0-1 BFS이다.
거울을 설치하는 것을 비용으로 정해, 거울이 설치되면 +1 그렇지 않으면 그냥 진행하는 식으로 진행한다.
문제의 요구사항은 가장 적게 거울을 사용해야 하는 것이므로 거울을 사용할 때는 deque의 뒤에 그렇지 않으면 deque의 앞에 추가한다.

#(0,3)에서 출발하여 아래칸(1,3)은 .이기 때문에 거울을 설치할 수 없다.
그렇기 때문에 deque의 앞에 추가한다.
또한, 방향을 바꿀 수 없기 때문에 직진만 한다.
이후, !인 칸(2,3)에 도착하면 왼쪽 혹은 오른쪽으로 방향을 변경할 수 있다.
하지만 오른쪽은 벽으로 막혀있기 때문에 진행할 수 없다.

만약, 왼쪽으로 이동한다면 거울을 설치한 것이기 때문에 deque의 뒤에 추가한다.
그렇지 않고, 직진했다면 deque의 앞에 추가한다.
이런 방법으로 BFS를 진행하며 최솟값을 갱신하고 최솟값보다 현재 거울의 개수가 많다면 더 이상 진행하지 않아도 된다.
이는 0-1 BFS의 특징인데, deque는 비용으로 정렬이 되어 있다.
비용이 늘어나는 것은 뒤쪽에 추가하기 때문에 비용이 적은 분기는 앞쪽에 있을 수밖에 없다.
즉, 최솟값보다 더 큰 비용이 나온 순간 그 뒤에있는 것들은 무조건 최솟값보다 더 많다는 뜻이다.
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
long long N;
bool IsInner(int y, int x)
{
return (y >= 0 && y < N && x >= 0 && x < N);
}
int BFS(vector<vector<char>>& Room, vector<pair<int, int>>& Doors)
{
int result = INT_MAX;
auto Start = Doors[0];
auto End = Doors[1];
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
vector<int> di = { 0, -1, 1 };
//y, x, dir, mirror
deque<tuple<int, int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, 0));
for (int i = 0; i < 4; i++)
{
int newY = Start.first + dy[i];
int newX = Start.second + dx[i];
if (!IsInner(newY, newX)) continue;
if (Room[newY][newX] == '*') continue;
dq.push_back({ Start.first, Start.second, i, 0 });
}
while (!dq.empty())
{
auto [y, x, dir, mirror] = dq.front();
dq.pop_front();
if (mirror >= result) break;
int iterCnt = Room[y][x] == '!' ? 3 : 1;
for (int i = 0; i < iterCnt; i++)
{
int newDir = (dir + di[i] + 4) % 4;
int addMirror = i > 0 ? 1 : 0;
int newY = y + dy[newDir];
int newX = x + dx[newDir];
if (!IsInner(newY, newX)) continue;
if (Room[newY][newX] == '*') continue;
if (newY == End.first && newX == End.second)
{
result = min(result, mirror+ addMirror);
continue;
}
if (addMirror == 1)
{
dq.push_back({ newY, newX, newDir, mirror+addMirror });
}
else
{
dq.push_front({ newY, newX, newDir, mirror });
}
}
}
return result;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<char>> Room(N, vector<char>(N));
vector<pair<int, int>> Doors;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> Room[i][j];
if (Room[i][j] == '#')
{
Doors.push_back({ i,j });
}
}
}
cout << BFS(Room, Doors);
return 0;
}