백준 1167 - 트리의 지름

 

 

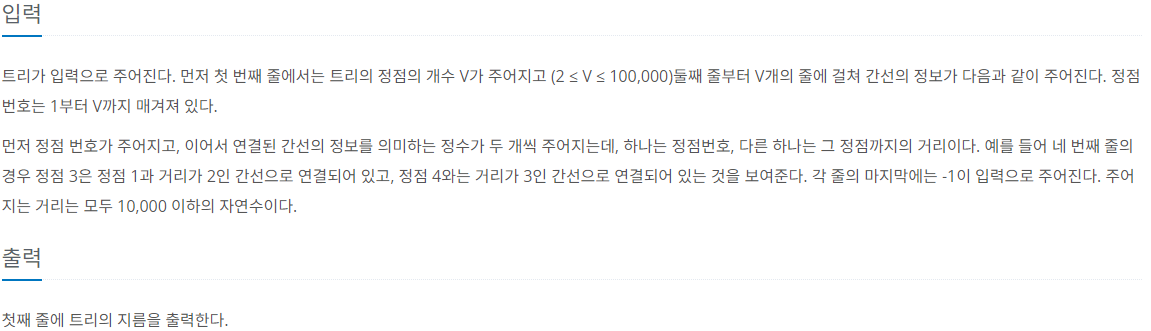
문제 설명

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

https://www.acmicpc.net/problem/1167

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, 트리의 지름을 구하는 것이다.

트리의 지름이란 트리에 있는 노드 간의 거리가 가장 먼 두 노드의 거리를 말한다.

트리의 지름을 구하는 방법은 크게 두 가지이다.

• DFS를 이용하는 방법
• DP를 이용하는 방법

DFS를 이용하는 방법은 간단하다.

임의의 노드를 고른 뒤 DFS를 통해 가장 먼 노드를 찾아낸다.

가장 먼 노드는 트리의 지름에 포함되는 노드이다.

따라서, 그 노드에서 가장 먼 노드를 다시 구하면 그 거리가 트리의 지름이 된다.

 

이를 증명하는 것은 간단하다.

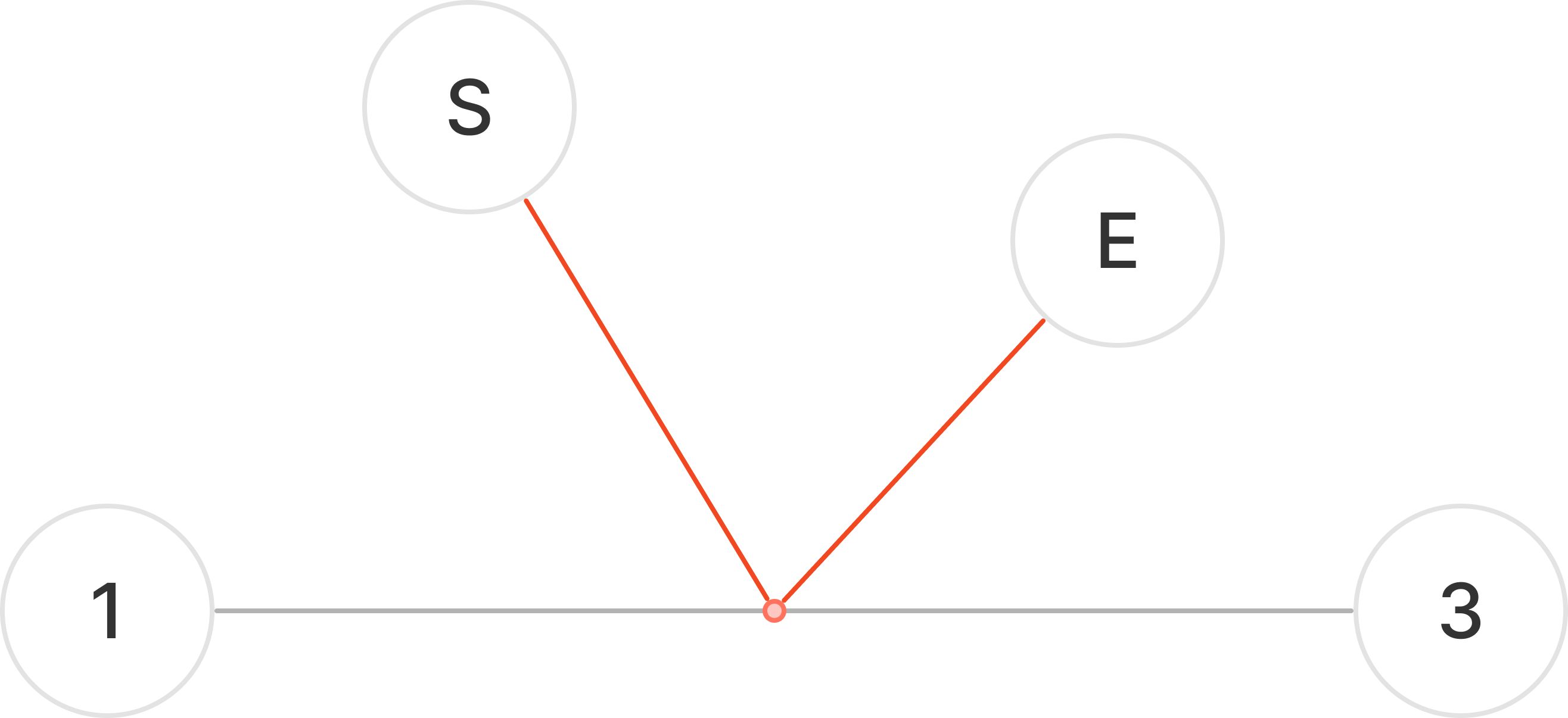
트리의 지름을 이루는 노드가 1과 3이라고 해 보자.

임의의 점 S에서 가장 먼 노드를 찾으면 1이나 3을 찾게 된다.

만약, E라고 한다면 지름이 1과 E로 이루어지기 때문에 모순이 된다.

 

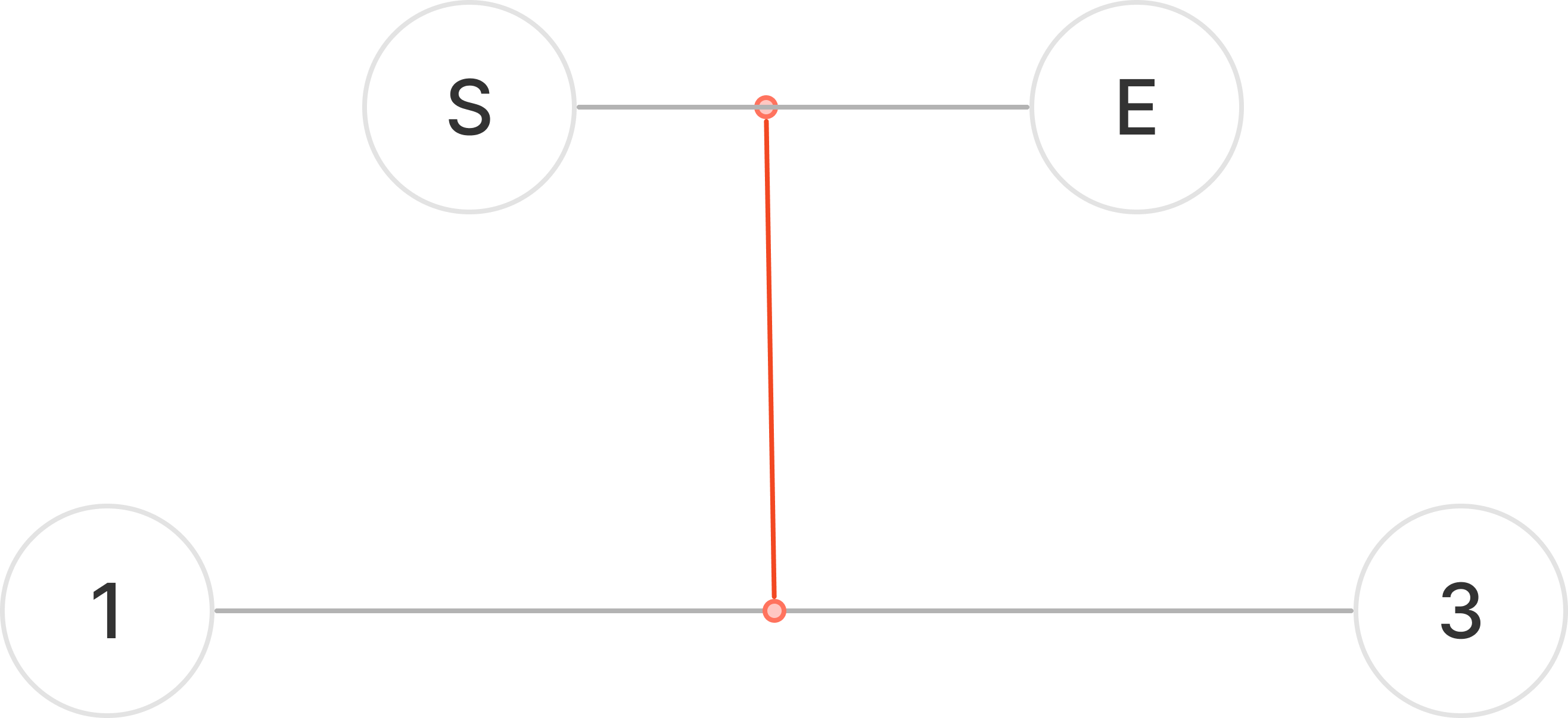
위와 같은 경우에도 성립한다.

1과 3이 지름을 이루고 있다면 S에서 가장 먼 노드를 찾게 되면 지름을 이루는 노드를 찾게 된다.

이 역시 그렇지 않게되면 지름이 바뀌기 때문이다.

 

정리하면 트리의 지름을 구하는 과정은 다음과 같다.

• 임의의 노드에서 DFS를 통해 가장 먼 노드를 찾는다
• 가장 먼 노드에서 DFS를 통해 또 가장 먼 노드를 찾는다.

먼 노드를 구하는 것은 BFS로도 가능하다.

하지만, 해당 문제에서는 메모리 초과가 발생해 DFS로 진행해야 한다.

int N;
int maxDist = 0;
int maxNode = 0;

void DFS(vector<vector<pair<int, int>>>& adj, vector<bool>& visited, int start, int dist)
{
    if (visited[start]) return;

    if (maxDist < dist)
    {
        maxDist = dist;
        maxNode = start;
    }

    visited[start] = true;
    for (auto [next, cost] : adj[start])
    {
        DFS(adj, visited, next, dist + cost);
    }
}

 

DP를 이용하는 방법은 아직까지는 잘 모르지만 정리하면 다음과 같다.

트리의 지름을 구하기 위해서는 두 가지를 구해야 한다.

• toLeaf(x): x가 루트일 때, 리프노드로 가는 가장 먼 거리
• maxLength(x): 가장 높은 지점이 x인 경로의 최대 길이

이는 모두 $O(N)$안에 계산할 수 있다.

toLeaf를 계산하기 위해서는 모든 자식 노드를 살펴보고 toLeft(c)가 최대인 자식 노드를 찾아 1을 더하면 된다.

즉, 재귀적으로 높이를 구하는 방식인 것 같다.

maxLength를 계산하기 위해서는 toLeaf(c1)+toLeaf(c2)이 되는 서로 다른 두 자식 노드를 찾은 뒤 그 값에 2를 더하면 된다.

예를 들어,

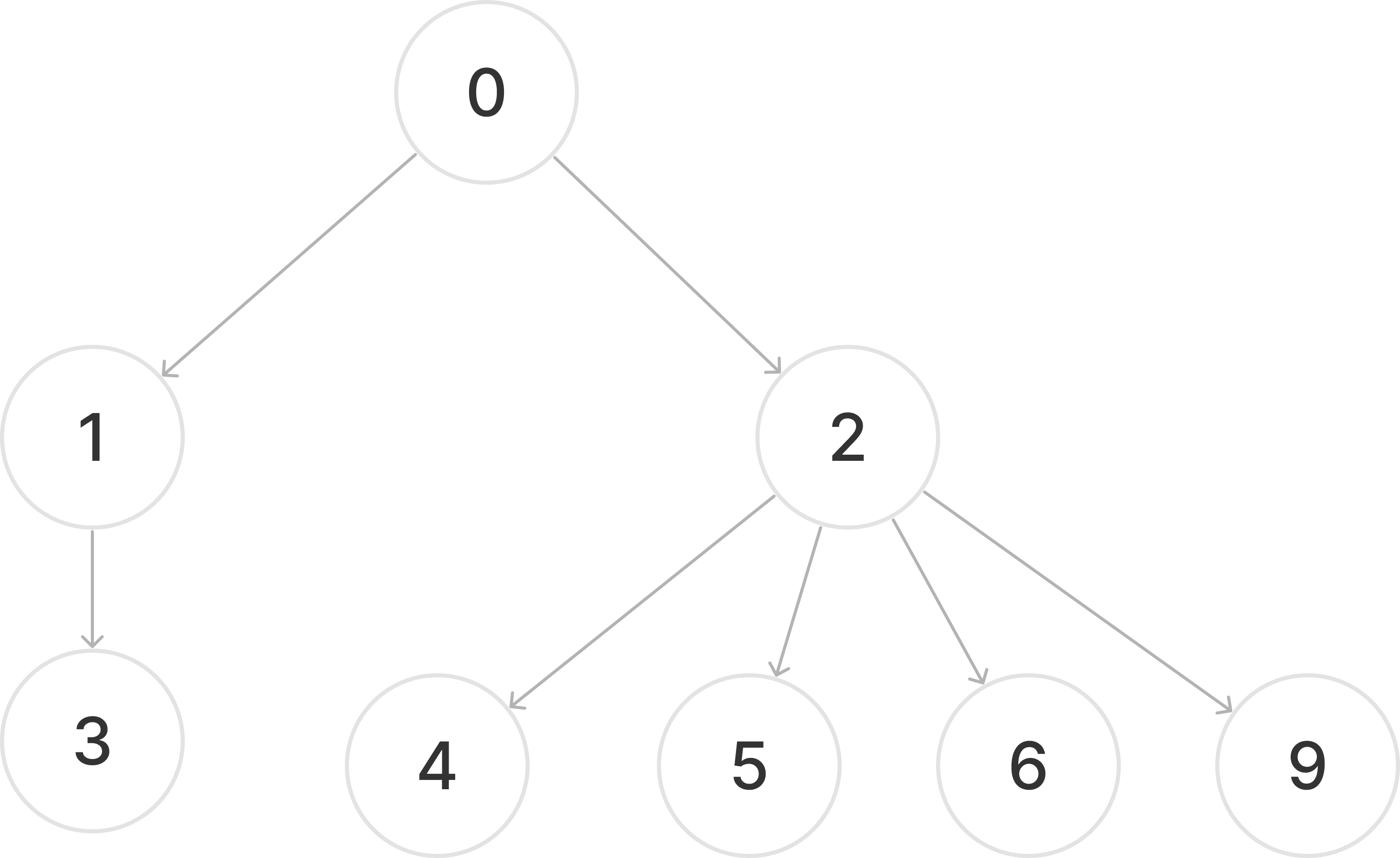
toLeaf(0)의 값은 2이다.

maxLength(0)의 값은 4이다.

이게 이론적으로는 이해가 되지만, 실제로 $O(N)$에 모든 노드에 대해 계산하는 것을 어떻게 구현해야 할지 감이 안 잡힌다.

대충 구현해 보면 다음과 같지 않을까 생각한다.

//x가 root일 때 i의 toLeaf값
toLeaf[x][i]

int toLeaf(int node)
{
    if (node == leaf) return 0;

    toLeaf[x][node] = 0;
    for (auto c : children)
    {
        toLeaf[x][node] = max(toLeaf[x][node], toLeaf(c));
    }
}


for(int i = 1; i <= N; i++)
{
	//가장 큰 두개 고르기
}

---

 

 

 

 

 

전체 코드

#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>

using namespace std;

int N;
int maxDist = 0;
int maxNode = 0;


void DFS(vector<vector<pair<int, int>>>& adj, vector<bool>& visited, int start, int dist)
{
    if (visited[start]) return;

    if (maxDist < dist)
    {
        maxDist = dist;
        maxNode = start;
    }

    visited[start] = true;
    for (auto [next, cost] : adj[start])
    {
        DFS(adj, visited, next, dist + cost);
    }
}

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> N;
    vector<vector<pair<int, int>>> adj(N+1);
    vector<bool> visited(N + 1, false);

    for (int i = 1; i <= N; i++)
    {
        int a, b, c;
        cin >> a;
        cin >> b;

        while (b != -1)
        {
            cin >> c;

            adj[a].push_back({ b,c });
            cin >> b;
        }
    }

    DFS(adj, visited, 1, 0);
    fill(visited.begin(), visited.end(), false);

    maxDist = 0;
    DFS(adj, visited, maxNode, 0);

    cout << maxDist;

    return 0;
}

---