백준 2042 - 구간 합 구하기

문제 설명

어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.

https://www.acmicpc.net/problem/2042

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, 트리에 대한 정보가 주어지고, M개의 쿼리가 주어지면 해당하는 연산을 하는 것이다.

쿼리의 종류로는 특정한 지점의 수를 변경하는 것과 주어진 구간의 곱을 출력하는 것이 있다.

 

해당 문제를 풀기 위해서는 구간 트리를 사용해야 한다.

구간 트리란 세그멘테이션 트리라고도 불리며 특정 구간의 쿼리에 맞는 연산을 수행한 결과를 나타내는 트리를 말한다.

예를 들어 보자.

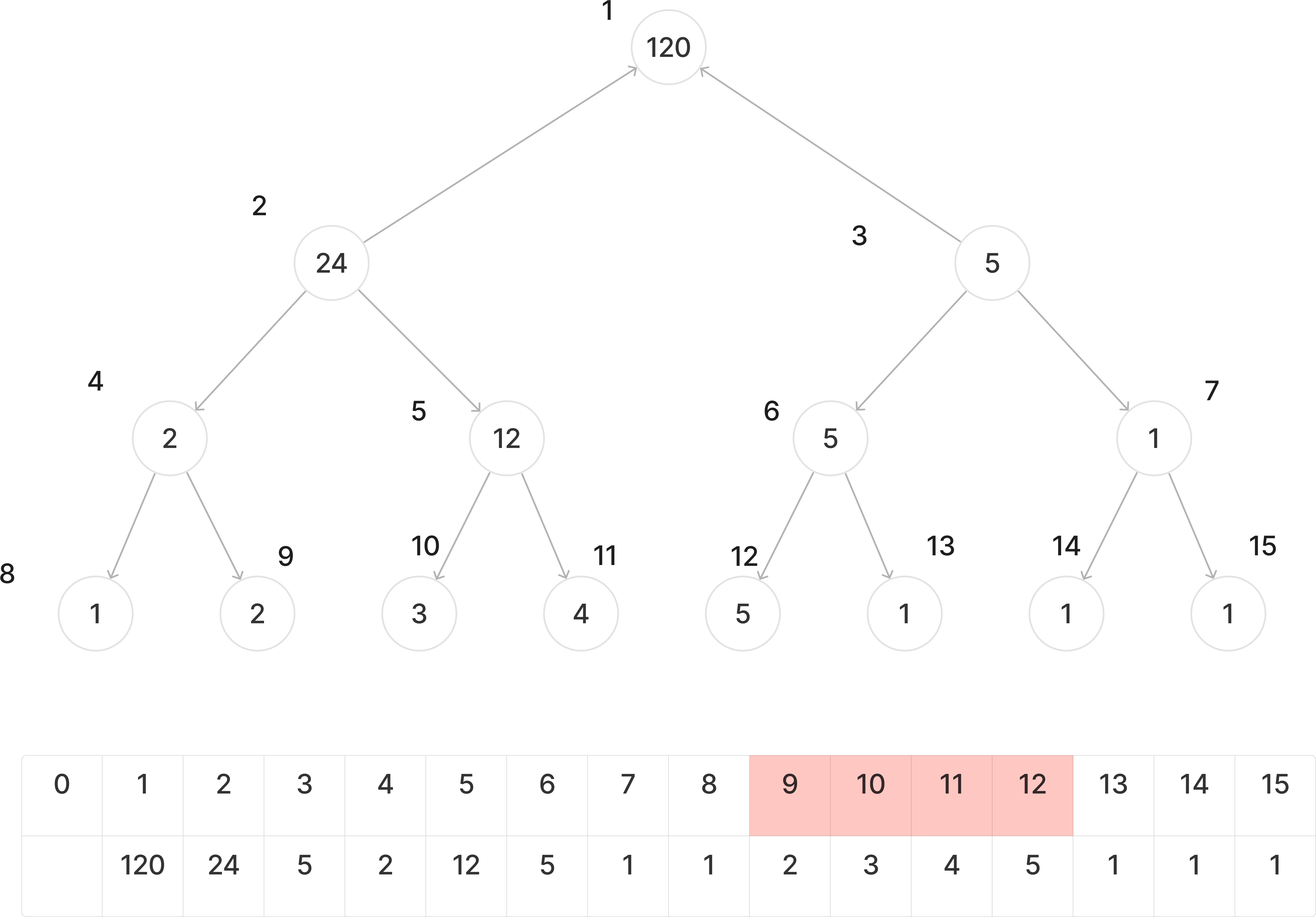
문제의 예시로 주어진 트리를 시각화한 것이다.

구간 트리는 위와같이 배열로 관리하는 것이 간편하다.

여기서 주의할 점은 구간 트리의 리프노드는 원래의 배열의 노드가 저장되어야 한다.

또한, $2^k$개의 개수로 맞추어야 한다.

예시에서는 5개의 노드가 있다. {1, 2, 3, 4, 5}

가장 가까운 $2^k$개는 8개이다.

따라서, 곱셈의 항등원인 1로 채워준다.

 

이후, 아래의 규칙에 의해 배열의 남은 칸이 채워진다.

tree[k] = tree[2*k] * tree[2*k+1]

이 규칙은 이진 트리의 특성을 이용한 것이다.

k의 왼쪽, 오른쪽 자식은 2*k, 2*k+1번째 노드이기 때문이다.

 

이렇게 tree배열을 세팅했다면, 쿼리를 처리하면 된다.

우선, 기존 값을 변경하는 쿼리를 처리해 보자.

기존 값은 트리의 N만큼 이동하여 저장되어 있다.

리프 노드에 저장되어야 하기 때문이다.

이때, N은 실제 N(5)이 아니라 $2^k$으로 맞춘 8 임을 주의해야 한다.

그렇다면 해당 부분을 X로 변경하고 부모를 타고가며 값을 변경해 주면 된다.

void ChangeNum(vector<long long>& Segment, int b, int c)
{
    b += scaledN;
    Segment[b] = c;
    for (b /= 2; b >= 1; b /= 2)
    {
        Segment[b] = Segment[2 * b] * Segment[2 * b + 1] % DIV;
    }
}

 

구간의 곱을 구하는 쿼리는 다음과 같이 처리한다.

구간의 시작 부분이 부모노드의 오른쪽 자식일 때, 부모 노드를 계산 결과에 추가하게 된다면 왼쪽 노드의 값이 딸려온다.

부모 노드는 왼쪽과 오른쪽 자식의 계산 결과이기 때문이다.

반대로, 구간의 끝 부분이 부모 노드의 왼쪽 자식이면 오른쪽 값이 딸려온다.

이러한 불필요한 부분을 제거하며 계속하여 부모로 옮기면 된다.

int GetMult(vector<long long>& Segment, int b, int c)
{
    b += scaledN;
    c += scaledN;

    int ans = 1;
    while (b <= c)
    {
        if (b % 2 == 1) ans = ans * Segment[b++] % DIV;
        if (c % 2 == 0) ans = ans * Segment[c--] % DIV;

        b /= 2;
        c /= 2;
    }

    return ans;
}

---

 

 

 

 

 

전체 코드

#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>

using namespace std;

int scaledN = 1, N, M, K;
const int DIV = 1'000'000'007;

void ChangeNum(vector<long long>& Segment, int b, int c)
{
    b += scaledN;
    Segment[b] = c;
    for (b /= 2; b >= 1; b /= 2)
    {
        Segment[b] = Segment[2 * b] * Segment[2 * b + 1] % DIV;
    }
}

int GetMult(vector<long long>& Segment, int b, int c)
{
    b += scaledN;
    c += scaledN;

    int ans = 1;
    while (b <= c)
    {
        if (b % 2 == 1) ans = ans * Segment[b++] % DIV;
        if (c % 2 == 0) ans = ans * Segment[c--] % DIV;

        b /= 2;
        c /= 2;
    }

    return ans;
}


int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M >> K;

    while (scaledN < N)
    {
        scaledN *= 2;
    }

    vector<long long> Segment(scaledN * 2, 1);

    for (int i = 0; i < N; i++)
    {
        cin >> Segment[i+ scaledN];
    }

    for (int i = scaledN - 1; i > 0; i--)
    {
        Segment[i] = Segment[2 * i] * Segment[2 * i + 1] % DIV;
    }

    for (int i = 0; i < M + K; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;

        if (a == 1)
        {
            ChangeNum(Segment, b-1, c);
        }
        else
        {
            cout << GetMult(Segment, b-1, c-1) << "\n";
        }
    }

    return 0;
}

---