문제 설명
인하대 컴퓨터 공학과에 재학 중인 이산이는 오랜만에 미팅을 나가 볼까 한다. 미팅은 N명이 원탁에 앉아서 진행된다고 한다. 질투가 난 이산이 친구 명기는 X의 저주를 걸었다. 그 저주는 N명이 동시에 2명씩 짝을 지어 악수할 때 사람의 팔이 교차되거나 한 사람이라도 악수를 하지 못하면 그 미팅은 실패하게 되는 저주다. 하지만 명기는 이산이에게 저주를 풀 기회를 주었다. 미팅에 성공할 경우의 수를 구하여 큰소리로 외치면 저주가 풀린다. 하지만 이산이는 계산 능력이 부족해서 당신에게 도움을 청했다. 이산이가 걸린 저주를 풀어주는 프로그램을 만들어주자.
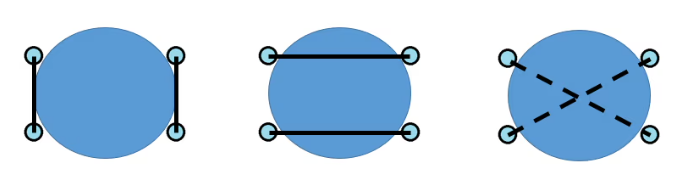
미팅에 참가한 사람이 4명일 경우 미팅에 성공할 경우는 다음 그림과 같이 2가지이다.
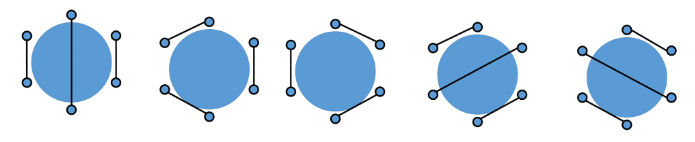
미팅에 참가한 사람이 6명일 경우 미팅에 성공할 경우는 다음 그림과 같이 5가지이다.
제한 사항


풀이
문제를 요약하면, N명이 악수를 하는데 서로 교차하지 않게 하는 방법의 개수를 찾아야 한다.
해당 문제는 카탈란 수를 통해 쉽게 구할 수 있다.
그렇다면, 왜 이 문제가 카탈란 수의 수열을 따라가는지 확인해 보자.
임의의 두 명이 악수를 한다고 가정해 보자.
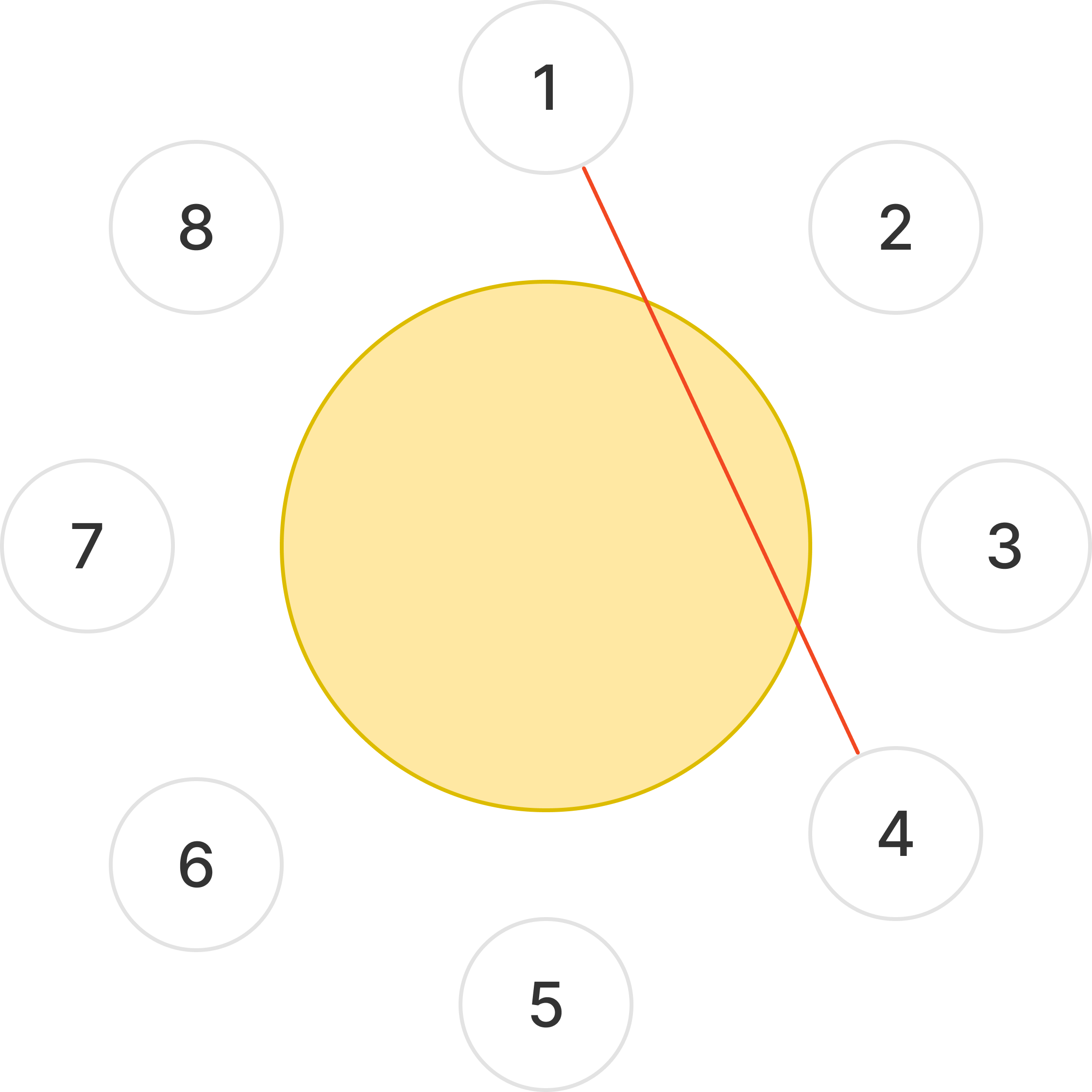
1번과 4번이 악수를 했다면, 8번과 3번은 악수할 수 없다.
악수를 하는 순간 겹치지 않기 위해서는 왼쪽과 오른쪽이 악수할 수 없다.
즉, 1번이 i번째 사람과 악수를 했다면, [2, i-1], [i+1, n] 두 개의 그룹으로 나눠진다.
그렇다면, 다음과 같이 정의할 수 있다.
- $C_i$: 1번부터 i번째까지 올바르게 악수를 했을 경우의 수
- $C_{n-i-1}$: i+1부터 n까지 올바르게 악수를 했을 경우의 수
이 두 가지의 곱으로 모든 경우의 수가 표현이 된다.
그리고 각 i에 대해 악수를 진행할 수 있으므로 최종적인 식은 다음과 같이 된다.
$$\sum_{i=1}^{ N-1 } C_iC_ {n-i-1} $$
이때, N은 쌍으로 계산한다.
N /= 2;
vector<long long> dp(N + 1, 0);
dp[0] = 1;
for (int i = 1; i <= N; i++)
{
for (int j = 0; j < i; j++)
{
dp[i] += dp[j] * dp[i - 1 - j] % DIV;
}
dp[i] %= DIV;
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
const int DIV = 987654321;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
N /= 2;
vector<long long> dp(N + 1, 0);
dp[0] = 1;
for (int i = 1; i <= N; i++)
{
for (int j = 0; j < i; j++)
{
dp[i] += dp[j] * dp[i - 1 - j] % DIV;
}
dp[i] %= DIV;
}
cout << dp[N];
return 0;
}