문제 설명
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
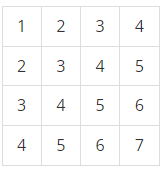
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/11660
제한 사항


풀이
문제를 요약하면, N x N 표가 주어지고 구간을 나타내는 좌표 (x1, y1), (x2, y2)가 주어질 때, 구간의 합을 구하는 문제이다.
1차원 구간합은 누적 합을 통해 쉽게 구해낼 수 있다.
2차원 구간합 역시 누적합으로 쉽게 구할 수 있다.
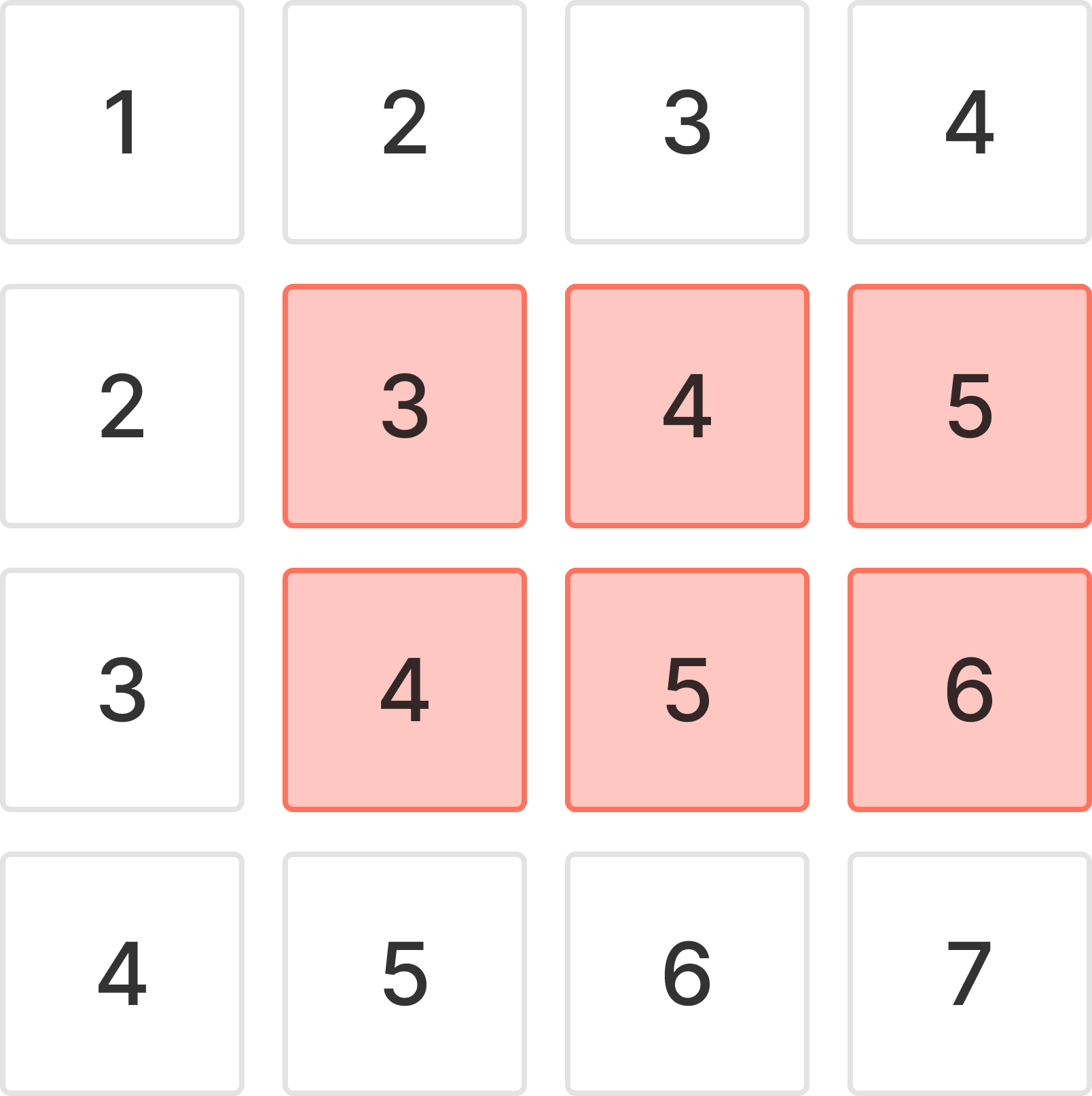
(2, 2)부터 (3, 4)까지의 구간 합을 구한다고 생각해 보자.
즉, 우리가 구해야 하는 것은 빨간 부분이다.
우선, 표를 누적합을 통해 구해내 보자.
누적합은 (1, 1)부터 (x, y)까지의 합을 구하는 것이다.
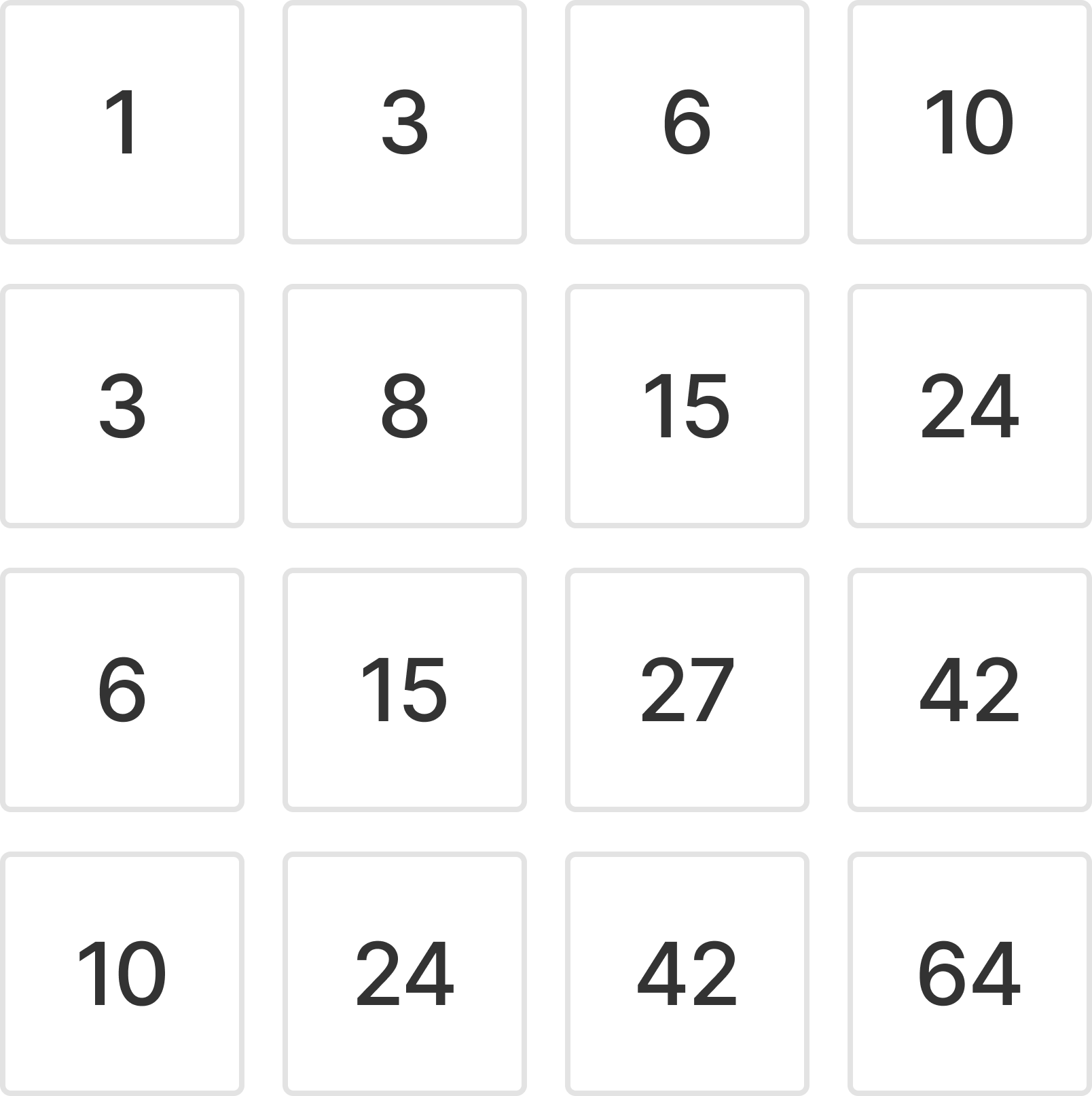
누적합을 구하면 위와 같은 결과가 나온다.
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
cin >> board[i][j];
sum[i][j] += sum[i][j - 1] + sum[i - 1][j] + board[i][j] - sum[i - 1][j - 1];
}
}자신의 위와 왼쪽을 더하고 대각선은 두 번 더해지기 때문에 한 번 빼주면 된다.
궁극적으로 우리가 구해야 하는 빨간 부분만의 누적합을 구하는 것은 다음과 같다.
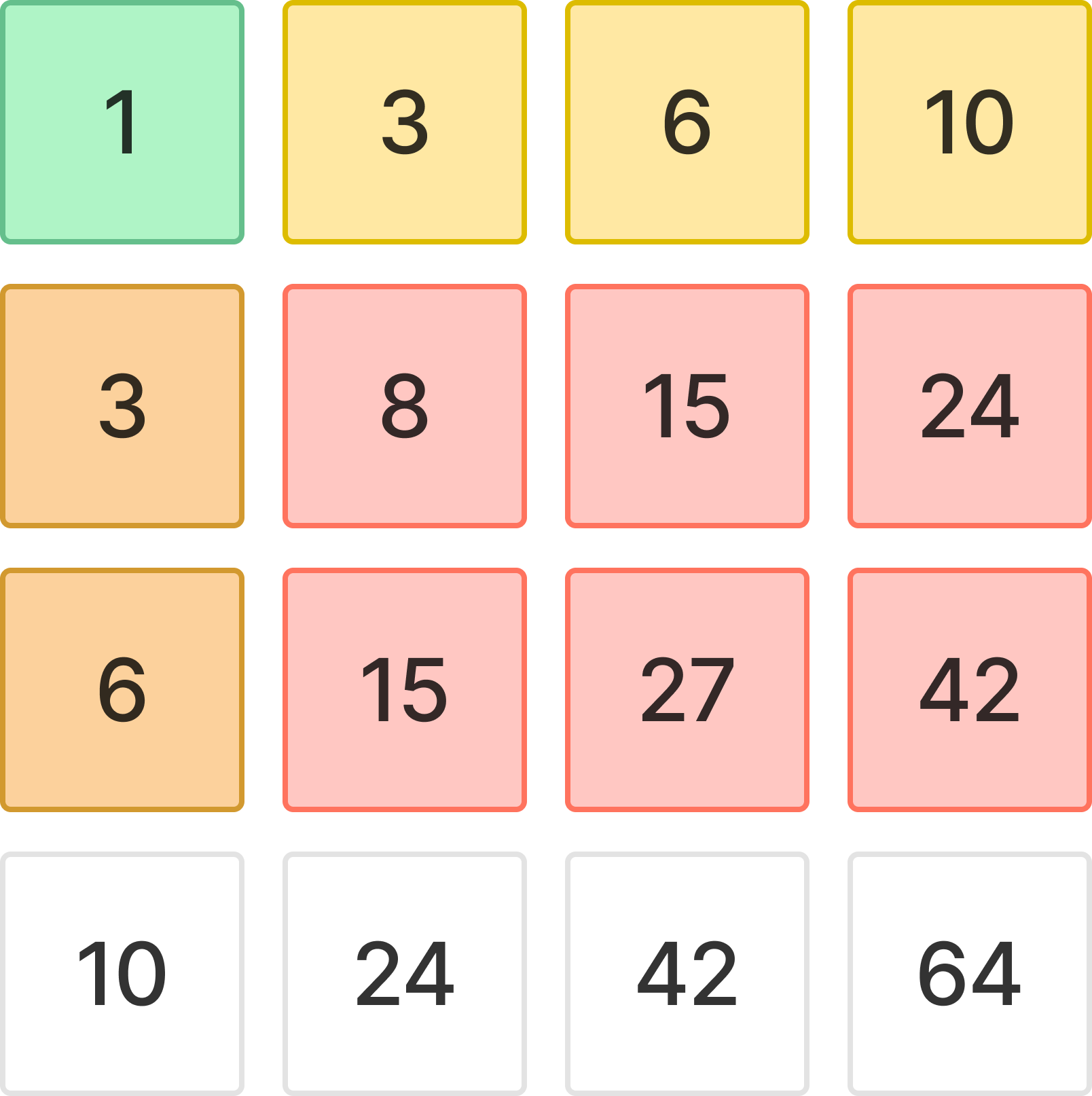
빨간 부분의 오른쪽 아래(42)는 (1, 1)부터 구해진 누적합이다.
(2, 2)부터 시작해야 하기 때문에 불필요한 부분은 제거해 주어야 한다.
따라서, (1, 1)부터 (1, 4)까지의 누적합과 (1, 1)부터 (3,1)까지의 누적합을 빼주어야 한다.
하지만, 그렇게 하면 (1, 1)이 두 번 빼지기 때문에 다시 한번 더해주어야 한다.
while (M--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] << "\n";
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N, M;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<int>> board(N+1, vector<int>(N+1));
vector<vector<int>> sum(N+1, vector<int>(N+1, 0));
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
cin >> board[i][j];
sum[i][j] += sum[i][j - 1] + sum[i - 1][j] + board[i][j] - sum[i - 1][j - 1];
}
}
while (M--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] << "\n";
}
return 0;
}
문제 설명
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/11660
제한 사항


풀이
문제를 요약하면, N x N 표가 주어지고 구간을 나타내는 좌표 (x1, y1), (x2, y2)가 주어질 때, 구간의 합을 구하는 문제이다.
1차원 구간합은 누적 합을 통해 쉽게 구해낼 수 있다.
2차원 구간합 역시 누적합으로 쉽게 구할 수 있다.

(2, 2)부터 (3, 4)까지의 구간 합을 구한다고 생각해 보자.
즉, 우리가 구해야 하는 것은 빨간 부분이다.
우선, 표를 누적합을 통해 구해내 보자.
누적합은 (1, 1)부터 (x, y)까지의 합을 구하는 것이다.

누적합을 구하면 위와 같은 결과가 나온다.
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
cin >> board[i][j];
sum[i][j] += sum[i][j - 1] + sum[i - 1][j] + board[i][j] - sum[i - 1][j - 1];
}
}자신의 위와 왼쪽을 더하고 대각선은 두 번 더해지기 때문에 한 번 빼주면 된다.
궁극적으로 우리가 구해야 하는 빨간 부분만의 누적합을 구하는 것은 다음과 같다.

빨간 부분의 오른쪽 아래(42)는 (1, 1)부터 구해진 누적합이다.
(2, 2)부터 시작해야 하기 때문에 불필요한 부분은 제거해 주어야 한다.
따라서, (1, 1)부터 (1, 4)까지의 누적합과 (1, 1)부터 (3,1)까지의 누적합을 빼주어야 한다.
하지만, 그렇게 하면 (1, 1)이 두 번 빼지기 때문에 다시 한번 더해주어야 한다.
while (M--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] << "\n";
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N, M;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<int>> board(N+1, vector<int>(N+1));
vector<vector<int>> sum(N+1, vector<int>(N+1, 0));
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
cin >> board[i][j];
sum[i][j] += sum[i][j - 1] + sum[i - 1][j] + board[i][j] - sum[i - 1][j - 1];
}
}
while (M--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] << "\n";
}
return 0;
}