문제 설명
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.
https://www.acmicpc.net/problem/11057
제한 사항


풀이
문제를 요약하면, i번째 숫자가 i-1번째보다 크거나 같은 수를 오르막 수라고 한다.
N이 주어지면 N자리 수의 오르막 수의 개수를 구하면 된다.
만약, i자리 수의 오르막 수의 개수를 안다면 i+1자리 수의 오르막 수의 개수를 구할 수 있다.
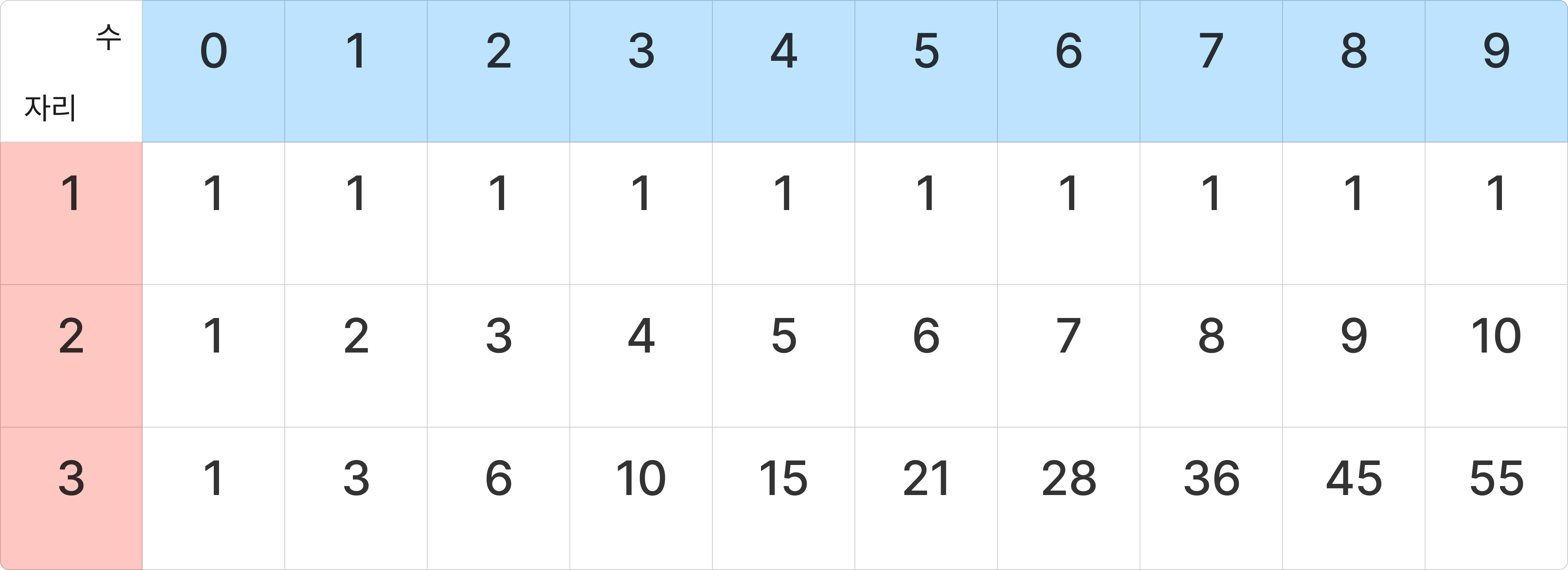
i자리의 수가 특정한 수로 끝난다고 가정을 하면 i-1자리 수 중 끝자리가 자신보다 낮은 수들에 자신을 더하면 오르막 수가 된다.
예를 들어, 2자리 오르막 수 중 5로 끝나는 수는 {15, 25, 35, 45, 55}가 된다.
즉, 5보다 작은 수들에 5를 더해 오르막 수를 구할 수 있다.
이러한 과정을 N까지 진행하면 정답을 구할 수 있다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
const int DIV = 10'007;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<int>> dp(N + 1, vector<int>(10, 0));
for (int i = 0; i <= 9; i++)
{
dp[1][i] = 1;
}
//i자리
for (int i = 2; i <= N; i++)
{
//j로 끝나는
for (int j = 0; j <= 9; j++)
{
for (int k = 0; k <= j; k++)
{
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % DIV;
}
}
}
int ans = 0;
for (int i = 0; i <= 9; i++)
{
ans = (ans + dp[N][i]) % DIV;
}
cout << ans;
return 0;
}
문제 설명
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.
https://www.acmicpc.net/problem/11057
제한 사항


풀이
문제를 요약하면, i번째 숫자가 i-1번째보다 크거나 같은 수를 오르막 수라고 한다.
N이 주어지면 N자리 수의 오르막 수의 개수를 구하면 된다.
만약, i자리 수의 오르막 수의 개수를 안다면 i+1자리 수의 오르막 수의 개수를 구할 수 있다.

i자리의 수가 특정한 수로 끝난다고 가정을 하면 i-1자리 수 중 끝자리가 자신보다 낮은 수들에 자신을 더하면 오르막 수가 된다.
예를 들어, 2자리 오르막 수 중 5로 끝나는 수는 {15, 25, 35, 45, 55}가 된다.
즉, 5보다 작은 수들에 5를 더해 오르막 수를 구할 수 있다.
이러한 과정을 N까지 진행하면 정답을 구할 수 있다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
const int DIV = 10'007;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<int>> dp(N + 1, vector<int>(10, 0));
for (int i = 0; i <= 9; i++)
{
dp[1][i] = 1;
}
//i자리
for (int i = 2; i <= N; i++)
{
//j로 끝나는
for (int j = 0; j <= 9; j++)
{
for (int k = 0; k <= j; k++)
{
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % DIV;
}
}
}
int ans = 0;
for (int i = 0; i <= 9; i++)
{
ans = (ans + dp[N][i]) % DIV;
}
cout << ans;
return 0;
}