문제 설명
어떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.

이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.
동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.
제한 사항


풀이
문제를 요약하면 2*N개의 칸의 사자를 배치하는데 가로, 세로가 연속하게 배치할 수 없다.
이때, 2*N칸의 사자를 배치할 수 있는 경우의 수를 구하면 된다.
N번째 칸에 사자를 배치하는 방법은 두 가지이다.
- N번째 칸에 사자를 배치할 경우
- N번째 칸에 사자를 배치하지 않을 경우
N번째 칸까지 사자를 배치하는 경우는 아래와 같다.
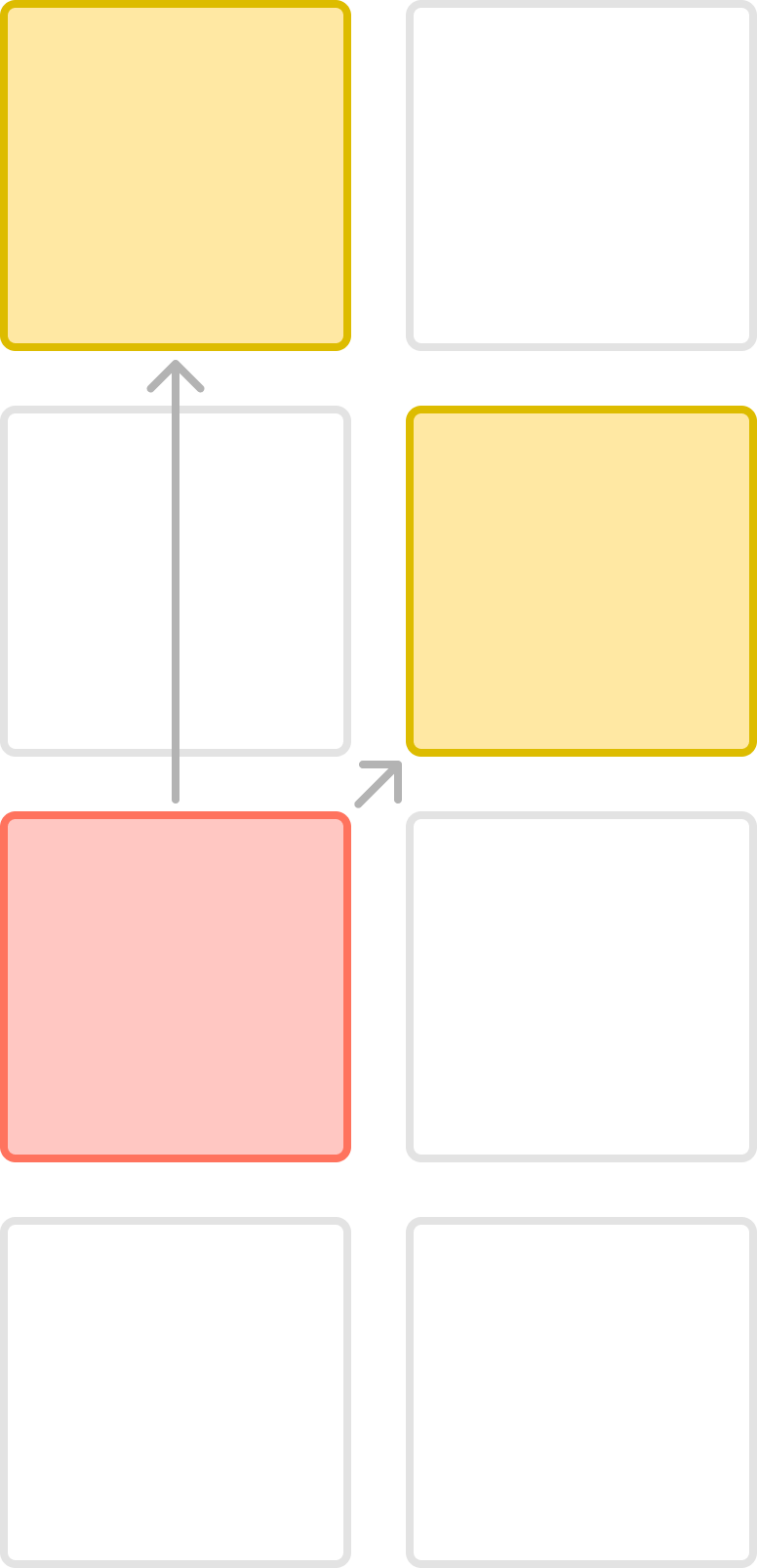
N번째 칸에 사자를 배치하지 않는다면 N-1번째 칸과 상관없다.
즉, N-1번째 왼쪽과 오른쪽의 경우의 수를 모두 더해야 한다.
N번째 칸에 사자를 배치한다면 N-1번째 칸에 사자가 있어서는 안 된다.
따라서, N-1번째 칸에 사자가 없다고 가정하고 N-2번째 칸의 경우를 더하면 된다.
dp[i] = (dp[i - 1] * 2 + dp[i - 2]) % DIV;
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
const int DIV = 9901;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<int> dp(N+1, 0);
dp[0] = 1;
dp[1] = 3;
for (int i = 2; i <= N; i++)
{
dp[i] = (dp[i - 1] * 2 + dp[i - 2]) % DIV;
}
cout << dp[N];
return 0;
}