문제 설명
N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다.
어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다. 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.
각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.
이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.
https://www.acmicpc.net/problem/1238
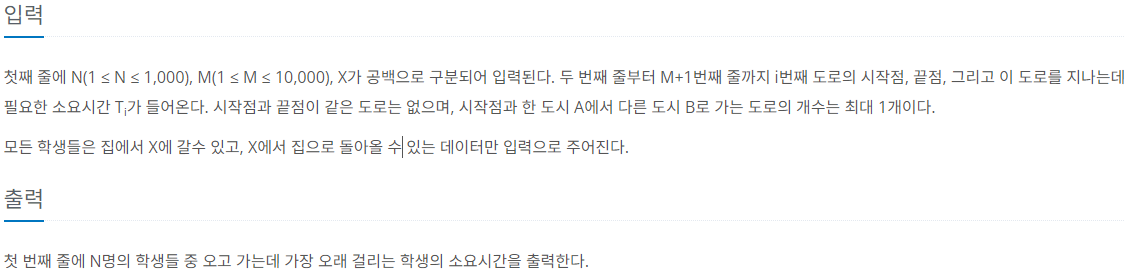
제한 사항

풀이
문제를 요약하면, N개의 노드가 있을 때 각 노드에서 X노드에 도착한 후 되돌아가는 경로가 가장 긴 노드의 이동거리를 구하는 것이다.
문제를 해결하는 방법은 여러 가지이다.
우선, N이 최대 1000이기 때문에 시간복잡도가 $O(N^3)$인 플로이드-와샬을 사용해도 충분히 해결가능하다.
for (int k = 1; k <= N; k++)
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
result[i][j] = min(result[i][j], result[i][k] + result[k][j]);
}
}
}
하지만, 시간이 오래걸린다.

시간을 줄이기 위해서는 한 가지 트릭을 사용하면 된다.
문제를 간단하게 만들어 보면, A → X → A가 최대인 노드를 구하면 되는 것이다.
우선, X → A는 구해내기 쉽다.
X노드를 시작으로 다익스트라를 한 번 진행하면 된다.
하지만, A → X가 문제이다.
각 노드를 시작으로 다익스트라를 진행해야 하는데 이렇게 하면 시간이 오래 걸릴 것이다.
여기서 트릭을 이용하면 최적화가 가능하다.
주어지는 그래프는 단방향 그래프이다.
주어지는 간선들을 역방향으로 조작하면 각 노드에서부터 X까지 이동하는 거리를 알 수 있다.
예를 들어 보자.
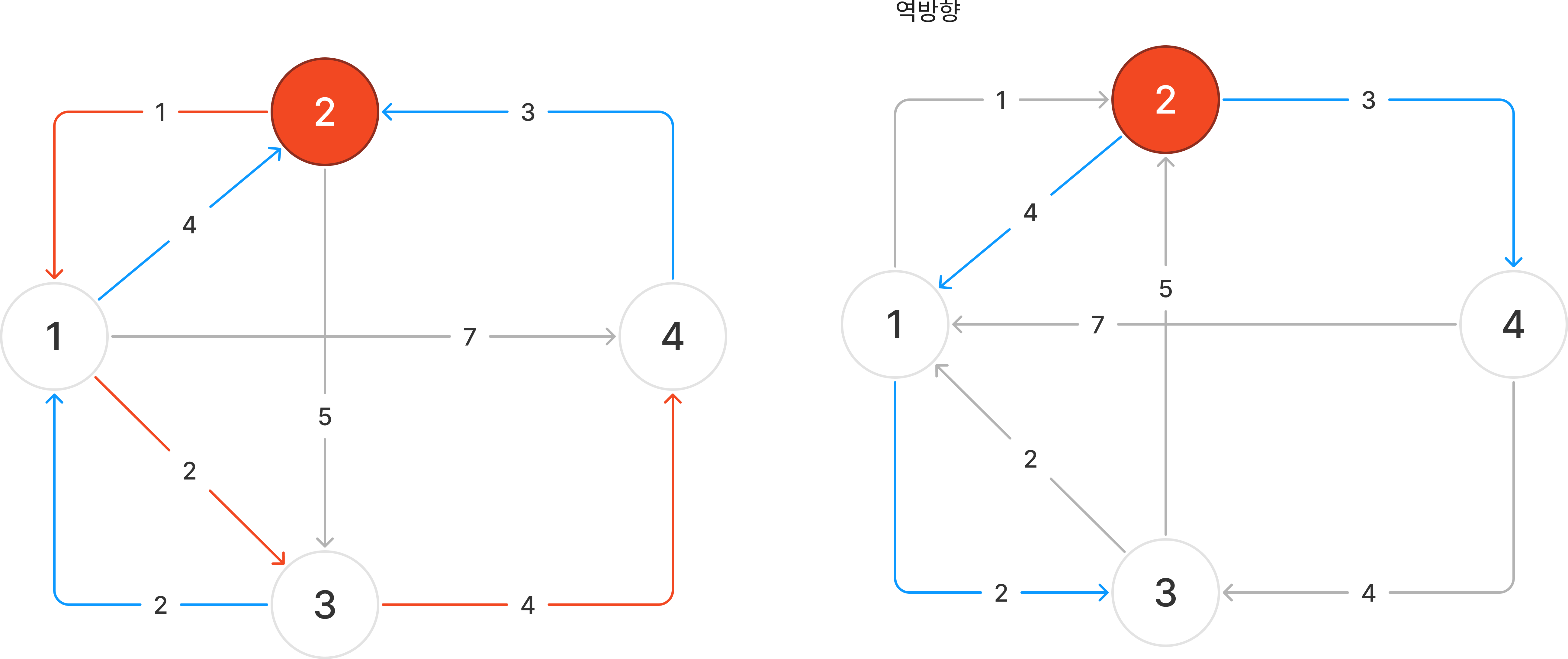
왼쪽이 주어진 그래프이고 오른쪽이 역방향으로 조작한 그래프이다.
역방향 그래프를 X에서 시작하는 다익스트라를 통해 각 노드까지의 최단 거리를 구하면 각 노드에서 시작하여 X에 도착하는 이동 거리를 구할 수 있다.
즉, 빨간 선은 X에서 각 노드로 돌아가는 간선이며 파란 선은 각 노드에서 X로 향하는 간선을 의미한다.
정리하면, 총 2번의 다익스트라를 진행한다.
한 번은 정방향 그래프를 이용해 X에서 시작하는 이동거리를 구한다. 이는 X에서 각 노드로 되돌아가는 이동 경로이다.
또 한 번은 역방향 그래프를 이용해 X에서 시작하는 이동거리를 구한다. 이는 각 노드에서 X로 향하는 이동 경로이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N, M, X;
vector<vector<pair<int, int>>> goRoads;
vector<vector<pair<int, int>>> backRoads;
vector<int> goDist;
vector<int> backDist;
const int MAX = 1000 * 100 + 1;
void Dijk(int start, vector<vector<pair<int, int>>>& roads, vector<int>& result)
{
//cost, dest
priority_queue<pair<int, int>> pq;
pq.push({ 0, start });
result[start] = 0;
while (!pq.empty())
{
auto [cost, dest] = pq.top();
pq.pop();
if (-cost < result[dest]) continue;
for (auto& [next, dist] : roads[dest])
{
if (result[next] > result[dest] + dist)
{
result[next] = result[dest] + dist;
pq.push({ -result[next], next });
}
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M >> X;
goRoads.resize(N + 1);
backRoads.resize(N + 1);
goDist.resize(N + 1, MAX);
backDist.resize(N + 1, MAX);
for (int i = 0; i < M; i++)
{
int a, b, c;
cin >> a >> b >> c;
backRoads[a].push_back({ b, c });
goRoads[b].push_back({ a, c });
}
//X번까지 왕복이 제일 긴 학생
//오고 가는 길이 다를 수 있음
Dijk(X, backRoads, backDist);
Dijk(X, goRoads, goDist);
int ans = 0;
for (int i = 1; i <= N; i++)
{
ans = max(ans, goDist[i] + backDist[i]);
}
cout << ans;
return 0;
}