문제 설명
성냥개비는 숫자를 나타내기에 아주 이상적인 도구이다. 보통 십진수를 성냥개비로 표현하는 방법은 다음과 같다.
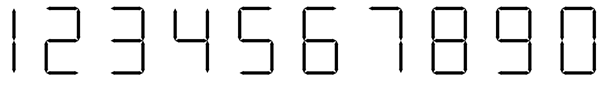
성냥개비의 개수가 주어졌을 때, 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 큰 수를 찾는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/3687
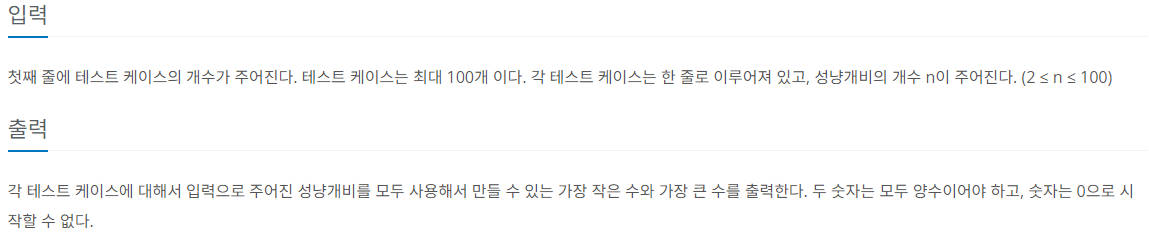
제한 사항

풀이
문제를 요약하면, N개의 성냥개비가 주어질 때, 만들 수 있는 가장 작은 수와 가장 큰수를 찾아내는 것이다.
처음 문제를 풀 때는 정해진 것과 변할 수 있는 것을 나누는 방식으로 접근하였다.
숫자 0~9를 만드는 성냥개비의 개수는 정해져 있다.
따라서, 각 경우에 대해 필요한 성냥개비의 개수를 미리 구해낸 뒤 이를 이용하여 수를 만들며 최소, 최대를 갱신하면 된다고 생각했다.
논리상 오류가 없고 예제도 통과하여 제출하였더니 시간 초과가 발생했다.
이는 최종적으로 수를 만들 때, 정렬을 통해 최소, 최대를 만들기 때문에 같은 집합이라면 동일한 연산을 중복하는 것이라 판단하여 방문체크를 통해 중복을 없애려 했다.
하지만, 이렇게 되면 메모리가 상당히 많이 필요하다고 생각했다.
따라서, 시간을 줄이기 위해서는 접근법을 바꿔야 했다.
보통 dfs, bfs는 dp로 변환이 가능하다.
해당 문제는 최소의 경우에만 dp로 변경하면 된다.
최대는 정해진 룰이 있기 때문이다.
최댓값을 만드는 방법은 최대한 적은 개수로 계속하여 자릿수를 늘리는 것이다.
즉, 2개의 성냥개비가 필요한 1을 계속하여 늘려 자릿수를 늘린 뒤 만약 주어진 N개의 성냥개비를 다썼다면 그대로 111...이 연속한 수가 만들어질 것이고 만약 3개가 남았다면 1이 아닌 7을 넣어주면 된다.
7은 총 3개의 성냥개비가 필요하며 7이 아닌 1을 추가한다 하더라도 1개의 성냥개비가 남아 더 이상 수를 추가할 수 없으므로 해당 경우에 7을 넣는 것이 최적해를 보장한다.
void makeMax(int num, vector<int>& nums)
{
if (num == 0) return;
if (num == 3)
{
nums.push_back(7);
return;
}
nums.push_back(1);
makeMax(num - 2, nums);
return;
}
그렇다면 이제 최솟값만 구하면 된다.
최솟값은 앞서 말했듯이 dp를 통해 구할 수 있다.
우선, 한 자리 수의 최솟값은 정해져 있다.
dp[1] = 9;
dp[2] = 1;
dp[3] = 7;
dp[4] = 4;
dp[5] = 2;
dp[6] = 6;
dp[7] = 8;dp[1]이 9인 이유는 1개의 성냥개비로 만들 수 있는 수가 없지만 이후 계산의 편의를 위해 임의의 최댓값을 넣어주었다.
이후, 8부터는 기록한 수를 이용하여 구해낼 수 있다.
만약, 8개로 한 자리 수를 만드는 것은 불가능하다.
그렇다면 두 자리 수를 만드려면 2개를 사용한 후 남은 6개로 만드는 방법, 3개 + 5개 등등 가능한 경우를 확인하며 dp를 채워나가면 된다.
단, dp에 기록된 것이 항상 가장 작은 값이 되는 것은 아니다.
예외가 발생하는 이유는 0때문이다.
문제에서 요구한 수의 범위는 자연수이기 때문에 0은 포함되지 않는다.
하지만, 두 번째 자릿수부터 0을 포함시킬 수 있다.
따라서, 최솟값을 유지하는 또 다른 배열을 통해 값을 계산해야 한다.
dp.resize(101, LLONG_MAX);
dp[1] = 9;
dp[2] = 1;
dp[3] = 7;
dp[4] = 4;
dp[5] = 2;
dp[6] = 6;
dp[7] = 8;
//makeMin
int minNums[8] = { 9,9,1,7,4,2,9,8 };
for (int i = 8; i <= 100; ++i)
{
for (int j = 2; j <= 7; ++j)
{
dp[i] = min(dp[i], dp[i - j] * 10 + minNums[j]);
}
}dp는 k개의 성냥개비로 만들 수 있는 가장 작은 수 이기 때문에 거기에 성냥개비 j개로 가장 작은 수를 만들어 더한 경우를 계산하여 dp를 갱신하는 것이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N, T;
vector<long long> dp;
void makeMax(int num, vector<int>& nums)
{
if (num == 0) return;
if (num == 3)
{
nums.push_back(7);
return;
}
nums.push_back(1);
makeMax(num - 2, nums);
return;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> T;
dp.resize(101, LLONG_MAX);
dp[1] = 9;
dp[2] = 1;
dp[3] = 7;
dp[4] = 4;
dp[5] = 2;
dp[6] = 6;
dp[7] = 8;
//makeMin
int minNums[8] = { 9,9,1,7,4,2,0,8 };
for (int i = 8; i <= 100; ++i)
{
for (int j = 2; j <= 7; ++j)
{
dp[i] = min(dp[i], dp[i - j] * 10 + minNums[j]);
}
}
for (int i = 0; i < T; i++)
{
cin >> N;
cout << dp[N] << " ";
//makeMax
vector<int> maxNums;
makeMax(N, maxNums);
for (auto itr = maxNums.rbegin(); itr != maxNums.rend(); itr++)
{
cout << *itr;
}
cout << "\n";
}
return 0;
}
