백준 1781 - 컵라면

 

문제 설명

상욱 조교는 동호에게 N개의 문제를 주고서, 각각의 문제를 풀었을 때 컵라면을 몇 개 줄 것인지 제시 하였다. 하지만 동호의 찌를듯한 자신감에 소심한 상욱 조교는 각각의 문제에 대해 데드라인을 정하였다.

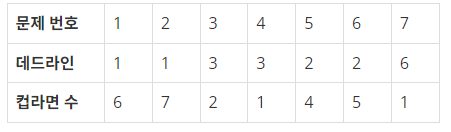
위와 같은 상황에서 동호가 2, 6, 3, 1, 7, 5, 4 순으로 숙제를 한다면 2, 6, 3, 7번 문제를 시간 내에 풀어 총 15개의 컵라면을 받을 수 있다.

문제는 동호가 받을 수 있는 최대 컵라면 수를 구하는 것이다. 위의 예에서는 15가 최대이다.

문제를 푸는데는 단위 시간 1이 걸리며, 각 문제의 데드라인은 N이하의 자연수이다. 또, 각 문제를 풀 때 받을 수 있는 컵라면 수와 최대로 받을 수 있는 컵라면 수는 모두 231보다 작은 자연수이다.

https://www.acmicpc.net/problem/1781

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, N개의 문제가 주어지고 해당 문제의 데드라인과 보상이 주어진다.

데드라인 안에 문제를 해결하면 보상을 받는다. 

하루에 문제를 하나씩 풀 때, 받을 수 있는 최대 보상을 구해야 한다.

 

해당 문제는 비슷한 문제로 가방에 최대 가치의 보석을 담는 문제인 백준 1202 - 보석 도둑을 푼적이 있어 접근법을 생각해 낼 수 있었다.

해당 문제는 그리디를 이용해서 접근해야 하는 문제이다.

간단하게 설명하면 보상을 획득 가능한 집합을 만들고 그 집합에서 최대 가치를 고르는 것이다.

그렇다면 보상을 획득 가능한 집합을 만들기만 하면 끝이다.

 

보상 획득 가능 집합은 데드라인을 넘기지 않고 문제를 해결할 수 있는 것들이다.

예를 들어,

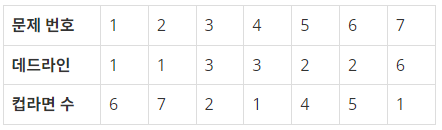
1일에 풀어 보상을 획득할 수 있는 문제는 1~7번 모든 문제이다.

2일에 풀어 보상을 획득할 수 있는 문제는 3~7번 문제이다.

시간순으로 후보군을 만들어 나가면 선택지가 점점 좁아지며 최적해를 구할 수 없다.

만약, 1일에 7번 문제를 풀었다면 데드라인이 1일인 문제는 보상을 받을 수 없기 때문이다.

즉, 해당 문제는 데드라인을 넘기지 않는 문제들을 후보군으로 설정해야 하기 때문에 시간의 역순으로 후보군을 만들어 가야 한다.

예를 들어 보자.

7일에 문제를 풀어 보상을 받을 수 있는 문제는 없으며, 6일에 풀어 보상을 받을 수 있는 문제는 7번 문제이다.

그렇다면, 6일까지의 최대 보상은 {7, X}로 문제를 풀었을 경우이다.

4, 5일 모두 보상을 받을 수 있는 문제는 없고 3일에 보상을 받을 수 있는 문제는 3, 4번이다.

이 중, 최댓값을 선택하면 3번문제가 될 것이다. {3, X, X, 7, X}

2일에 보상을 획득할 수 있는 문제는 5, 6번이다. 마찬가지로 최대 보상을 선택하면 {6, 3, X, X, 7, X}이 된다.

1일도 마찬가지로 진행하면 {2, 6, 3, X, X, 7, X}가 된다.

이때, X에는 선택되지 않은 어떤 수가 들어가도 상관이 없으며 7의 위치도 X와 변경되어도 된다.

정리하자면, 데드라인의 끝( 시간의 마지막 = N )부터 진행하며 해당 날짜까지 보상을 받을 수 있는 문제들을 모두 pq에 넣은 뒤 최댓값을 뽑아 더해주면 된다.

단, 논리대로 진행되기 위해서는 우선적으로 데드라인 순으로 정렬이 되어야 한다.

---

 

 

 

 

 

전체 코드

#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <list>
#include <bitset>

using namespace std;

int N;
vector<pair<int, int>> problems;

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cout.precision(4);

    cin >> N;
    problems.resize(N + 1);

    for (int i = 1; i <= N; i++)
    {
        int a, b;
        cin >> a >> b;

        //{deadline, reward}
        problems[i] = { a,b };
    }

    sort(problems.begin(), problems.end());

    int idx = N;
    long long ans = 0;

    priority_queue<int> pq;

    for (int i = N; i > 0; i--)
    {
        while (idx > 0 && problems[idx].first >= i)
        {
            pq.push(problems[idx].second);
            idx--;
        }

        if (pq.empty()) continue;
        
        ans += pq.top();
        pq.pop();
    }

    cout << ans;

    return 0;
}

 

---