문제 설명
아래의 그림과 같이 배열된 장애물들 사이로, 구슬을 굴린다.
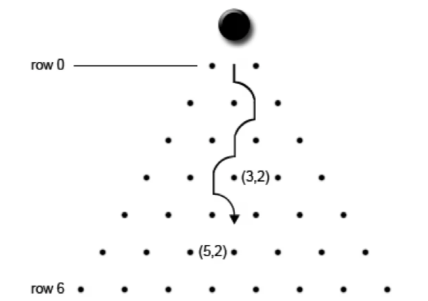
장애물들은 n개의 행에 걸쳐 배치되어 있으며, 구슬은 맨 위의 행부터 맨 아래의 행을 향해 구른다. 각 행의 장애물들을 지나면서, 구슬은 왼쪽 또는 오른쪽으로 굴러갈 수 있다. 각 행의 번호는 0부터 n-1까지로 주어지며, 그 행의 장애물 사이의 공간은 왼쪽부터 차례로 0으로 주어진다.
(0, 0)의 위치에서부터 아래로 구슬을 굴려갈 때, n-1번 행까지 구슬을 굴리는 경우의 수를 구하는 프로그램을 작성하시오. 단, 구슬은 주어진 m개의 공간을 모두 지나야 한다.
https://www.acmicpc.net/problem/23317
제한 사항

풀이
문제를 요약하면, 주어진 좌표에 해당하는 빈칸을 모두 통과하여 바닥까지 떨어지는 경우의 수를 구하는 것이다.
우선, 좌표가 없이 떨어지는 모든 경우의 수를 구한다고 생각해 보자.
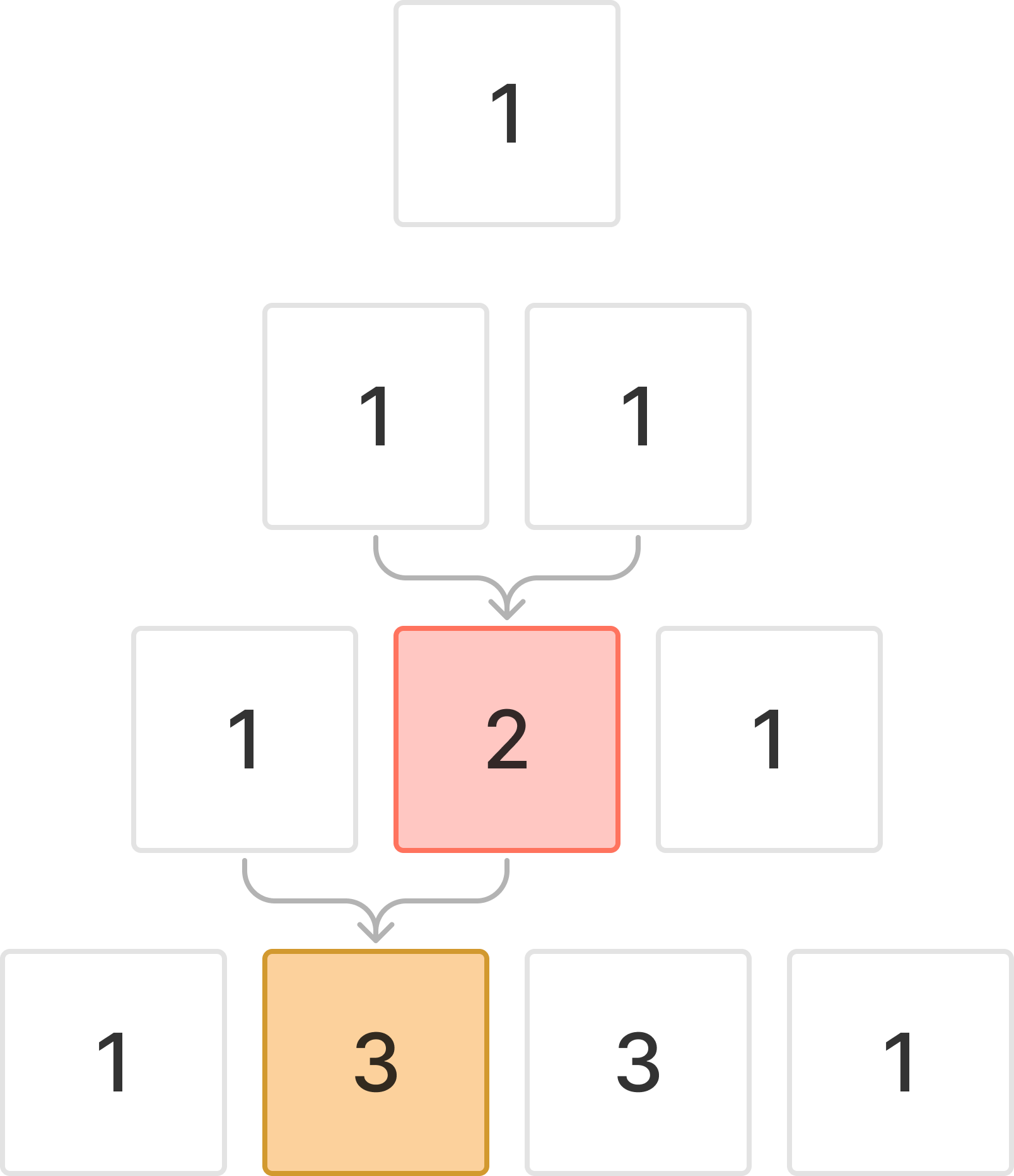
그렇다면, 제일 위칸은 무조건 1가지의 경우의 수만 존재할 것이다.
그 아랫줄은 총 2개의 빈칸이 있으며 각각 1가지의 경우의 수가 존재한다.
그 밑줄은 각각 1, 2, 1의 경우의 수가 생긴다.
가운데 칸은 자신의 왼쪽 위칸, 오른쪽 위칸에서 모두 떨어질 수 있기에 두 경우를 합해야 한다.
그 경우의 수가 아래까지 전달 된다.
그럼, 좌표가 지정되어 있는 칸을 무조건 지나야 한다고 하면 같은 줄에 있는 다른 빈칸은 지날 수 없다.
즉, 같은 줄에 있는 좌표와 다른 칸을 지나는 경우의 수를 0으로 기록한 뒤 아랫줄부터 다시 같은 과정을 진행하면 된다.
7
2
3 2
5 2이러한 경우의 배열 형태를 살펴보자.
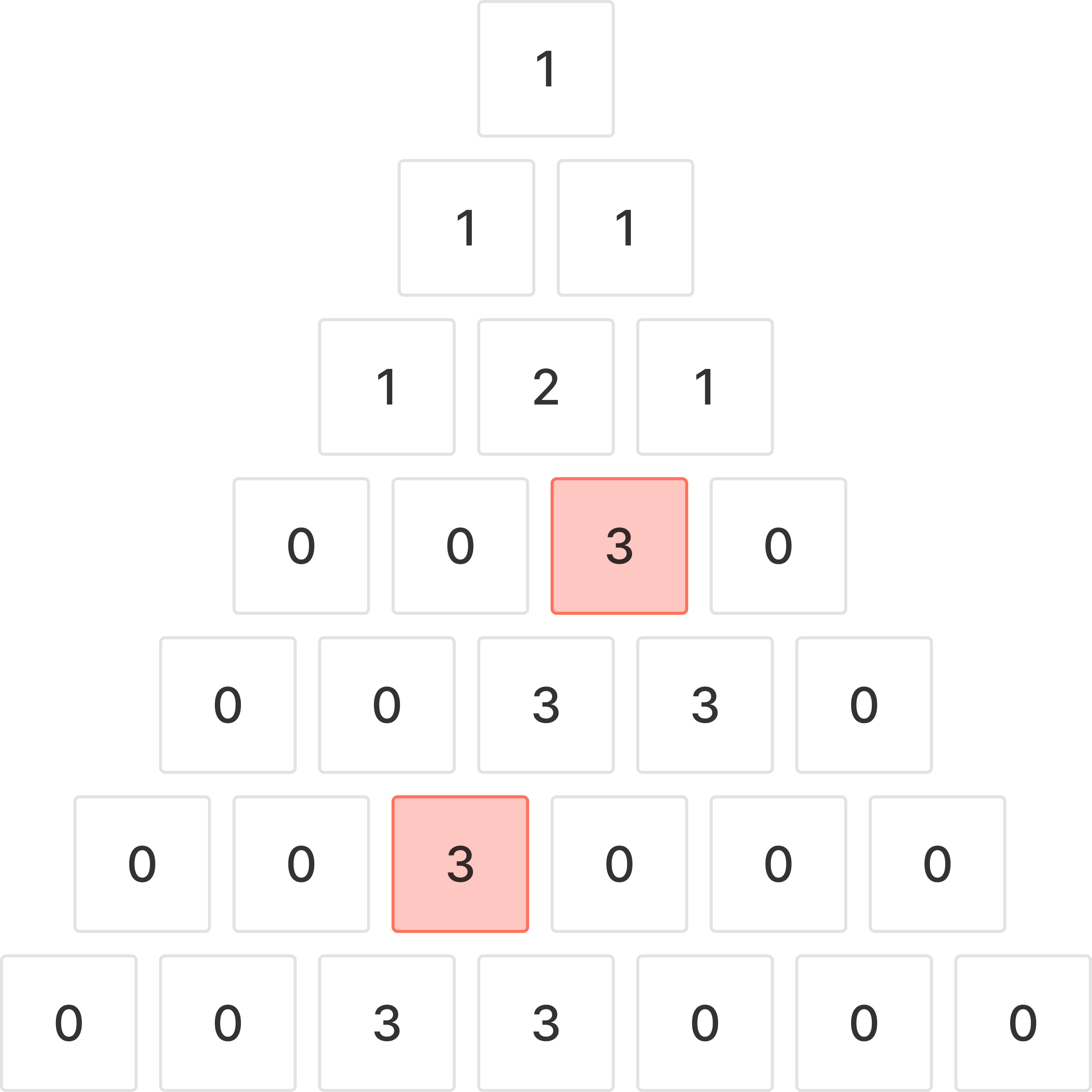
빨간 칸이 꼭 지나야 하는 칸이다.
꼭 지나야 하는 칸을 모두 지나왔다면, 바닥까지 떨어지는 경우의 수를 모두 구해 다 더해주면 된다.
여기서 주의할 점은 입력에 주어지는 좌표가 동일한 좌표를 입력받을 수 있다.
또한, 위와 같은 논리가 적용되기 위해서는 위에서부터 진행해야 하기 때문에 좌표가 정렬된 상태를 유지해야 한다.
따라서, 이에 부합하는 set을 이용하는 것이 좋다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<vector<int>> dp(N, vector<int>(N, 0));
set<pair<int, int>> points;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
points.insert({ a,b });
}
dp[0][0] = 1;
int row = 1;
for (auto itr = points.begin(); itr != points.end(); itr++)
{
auto [y, x] = *itr;
for (; row <= y; row++)
{
for (int j = 0; j <= row; j++)
{
dp[row][j] += dp[row - 1][j];
if (j - 1 >= 0)
{
dp[row][j] += dp[row - 1][j - 1];
}
if (row == y && j != x) dp[row][j] = 0;
}
}
}
long long ans = 0;
for (int i = row; i < N; i++)
{
for (int j = 0; j <= i; j++)
{
dp[i][j] += dp[i - 1][j];
if (j - 1 >= 0)
{
dp[i][j] += dp[i - 1][j - 1];
}
if (i == N - 1) ans += dp[i][j];
}
}
cout << ans;
return 0;
}