문제 설명
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.
여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최솟값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.
https://www.acmicpc.net/problem/10868
제한 사항


풀이
문제를 요약하면, (a, b)구간의 최솟값을 구하는 쿼리를 M번 수행하면 된다.
M이 최대 100,000이기 때문에 $O(N^2)$으로는 시간 초과가 발생한다.
해당 문제는 세그먼트 트리를 이용하면 쉽게 풀 수 있다.
세그먼트 트리란, 원래의 배열을 리프 노드로 하는 이진 트리를 말한다.
각 부모 노드는 자식 노드에 대한 쿼리를 진행한 결과를 기록하면 된다.
해당 문제에서는 최솟값을 구하는 쿼리를 요구하므로 부모 노드에 최솟값을 기록하면 된다.
예를 들어 보자.
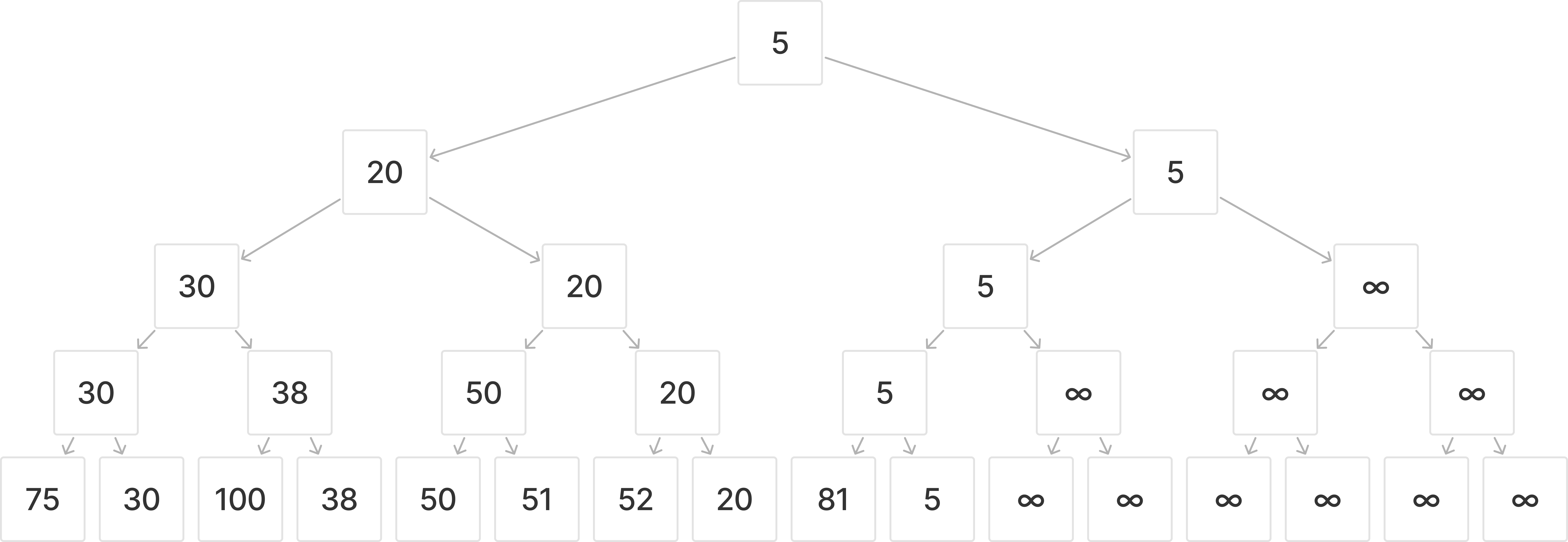
세그먼트 트리는 포화 이진 트리이기 때문에 $2^k$개의 리프노트가 필요하다.
이렇게 구성된 트리는 다음과 같은 특징을 갖는다.
- 왼쪽 자식: 2 * k
- 오른쪽 자식: 2 * k + 1
- 부모: k / 2
세그먼트 트리는 쿼리를 자식에 대해서만 처리한 뒤 루트 노드까지 진행하기 때문에 쿼리를 $O(logN)$안에 처리할 수 있다는 것이다.
또한, 리프 노드를 갱신하는 것도 $O(logN)$안에 처리할 수 있다.
이 역시, 자신의 부모로만 전달하면 되기 때문이다.
우선 노드의 상태를 업데이트하는 함수부터 봐 보자.
void update(int idx)
{
int converted = (idx + leafSize) / 2;
while (converted >= 1)
{
seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
converted /= 2;
}
}리프 노드의 사이즈만큼 인덱스를 옮긴 뒤, 루트까지 갱신하면 된다.
쿼리를 처리하는 함수는 다음과 같다.
int getMin(int a, int b)
{
int left = a + leafSize;
int right = b + leafSize;
int result = INT_MAX;
while (left <= right)
{
if (left % 2 == 1) result = min(result, seg[left++]);
if (right % 2 == 0) result = min(result, seg[right--]);
left /= 2;
right /= 2;
}
return result;
}왼쪽 인덱스가 홀수라면 해당 노드의 부모는 (a, b)에 포함하지 않는 a-1까지 포함하여 계산하게 된다.
따라서, 미리 계산한 뒤 부모로 옮긴다.
오른쪽 인덱스는 반대로 생각하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> nums;
vector<int> seg;
int leafSize = 1;
void update(int idx)
{
int converted = (idx + leafSize) / 2;
while (converted >= 1)
{
seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
converted /= 2;
}
}
int getMin(int a, int b)
{
int left = a + leafSize;
int right = b + leafSize;
int result = INT_MAX;
while (left <= right)
{
if (left % 2 == 1) result = min(result, seg[left++]);
if (right % 2 == 0) result = min(result, seg[right--]);
left /= 2;
right /= 2;
}
return result;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
while (leafSize < N)
{
leafSize *= 2;
}
seg.resize(2 * leafSize + 1, INT_MAX);
nums.resize(N + 1);
for (int i = 1; i <= N; i++)
{
cin >> nums[i];
seg[leafSize + i] = nums[i];
}
for (int i = 1; i <= N; i += 2)
{
update(i);
}
vector<pair<int, int>> querise;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
cout << getMin(a, b) << "\n";
}
return 0;
}
문제 설명
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.
여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최솟값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.
https://www.acmicpc.net/problem/10868
제한 사항


풀이
문제를 요약하면, (a, b)구간의 최솟값을 구하는 쿼리를 M번 수행하면 된다.
M이 최대 100,000이기 때문에
해당 문제는 세그먼트 트리를 이용하면 쉽게 풀 수 있다.
세그먼트 트리란, 원래의 배열을 리프 노드로 하는 이진 트리를 말한다.
각 부모 노드는 자식 노드에 대한 쿼리를 진행한 결과를 기록하면 된다.
해당 문제에서는 최솟값을 구하는 쿼리를 요구하므로 부모 노드에 최솟값을 기록하면 된다.
예를 들어 보자.

세그먼트 트리는 포화 이진 트리이기 때문에
이렇게 구성된 트리는 다음과 같은 특징을 갖는다.
- 왼쪽 자식: 2 * k
- 오른쪽 자식: 2 * k + 1
- 부모: k / 2
세그먼트 트리는 쿼리를 자식에 대해서만 처리한 뒤 루트 노드까지 진행하기 때문에 쿼리를
또한, 리프 노드를 갱신하는 것도
이 역시, 자신의 부모로만 전달하면 되기 때문이다.
우선 노드의 상태를 업데이트하는 함수부터 봐 보자.
void update(int idx)
{
int converted = (idx + leafSize) / 2;
while (converted >= 1)
{
seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
converted /= 2;
}
}리프 노드의 사이즈만큼 인덱스를 옮긴 뒤, 루트까지 갱신하면 된다.
쿼리를 처리하는 함수는 다음과 같다.
int getMin(int a, int b)
{
int left = a + leafSize;
int right = b + leafSize;
int result = INT_MAX;
while (left <= right)
{
if (left % 2 == 1) result = min(result, seg[left++]);
if (right % 2 == 0) result = min(result, seg[right--]);
left /= 2;
right /= 2;
}
return result;
}왼쪽 인덱스가 홀수라면 해당 노드의 부모는 (a, b)에 포함하지 않는 a-1까지 포함하여 계산하게 된다.
따라서, 미리 계산한 뒤 부모로 옮긴다.
오른쪽 인덱스는 반대로 생각하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> nums;
vector<int> seg;
int leafSize = 1;
void update(int idx)
{
int converted = (idx + leafSize) / 2;
while (converted >= 1)
{
seg[converted] = min(seg[converted * 2], seg[converted * 2 + 1]);
converted /= 2;
}
}
int getMin(int a, int b)
{
int left = a + leafSize;
int right = b + leafSize;
int result = INT_MAX;
while (left <= right)
{
if (left % 2 == 1) result = min(result, seg[left++]);
if (right % 2 == 0) result = min(result, seg[right--]);
left /= 2;
right /= 2;
}
return result;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
while (leafSize < N)
{
leafSize *= 2;
}
seg.resize(2 * leafSize + 1, INT_MAX);
nums.resize(N + 1);
for (int i = 1; i <= N; i++)
{
cin >> nums[i];
seg[leafSize + i] = nums[i];
}
for (int i = 1; i <= N; i += 2)
{
update(i);
}
vector<pair<int, int>> querise;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
cout << getMin(a, b) << "\n";
}
return 0;
}