문제 설명
지금 구두 수선공에게는 손님으로부터 주문 받고 제작해야 할 작업이 N개 쌓여있다. 구두 수선공은 하루에 한 작업만 수행할 수 있고, i번째 작업을 완료하는 데 Ti일이 걸린다. 이때 Ti는 정수이고 1 ≤ Ti ≤ 1000이다.
i번째 작업을 시작하기 전에 하루가 지연될 때마다 구두 수선공은 보상금 Si센트를 지불해야 한다. 이때 Si는 정수이고 1 ≤ Si ≤ 10000이다. 구두 수선공을 돕기 위해 최저 보상금을 지불하는 작업 순서를 정해야 한다.
하루에 2개 이상의 작업을 동시에 수행할 수 없다. 작업 i를 수행하고 있는 경우, 작업 i를 마칠 때 까지 작업 i 외의 다른 작업을 수행할 수 없다.
https://www.acmicpc.net/problem/14908
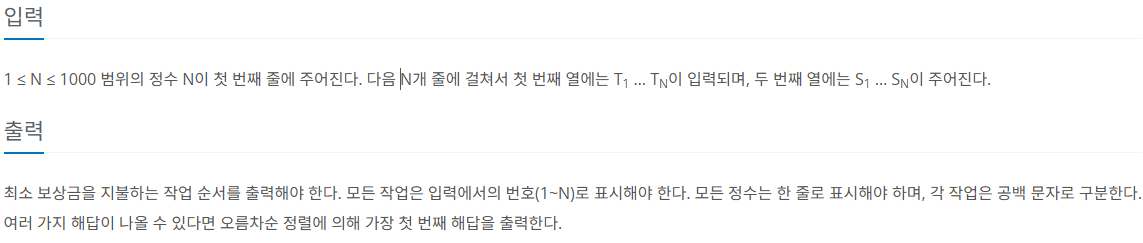
제한 사항

풀이
문제를 요약하면, T시간이 걸리는 작업을 모두 수행해야 한다.
만약 작업이 다른 작업에 의해 지연되는 경우 하루마다 S원씩 보상금을 주어야 할 때 보상금을 최소로 하는 작업 순서를 구해야 한다.
처음에는 해당 문제를 dp로 접근해 봤다.
i번째 작업까지만 존재한다고 가정했을 때, j시간에서 보상해야 하는 보상금의 최솟값을 구하려 해 봤다.
하지만, 점화식을 세우기 쉽지 않았다.
해당 문제는 다르게 접근해야 했다.
우선, 작업의 데드라인을 d라고 하고 실제로 작업이 완료되는 날을 x라고 해보자.
그렇다면, (x-d) * S만큼의 보상금을 지불해야 한다.
이러한 상황에서 전체 보상금을 적게 만들기 위해서는 하루당 보상금을 최대한 적게 만드는 것이 좋다.
4
3 4
1 1000
2 2
5 5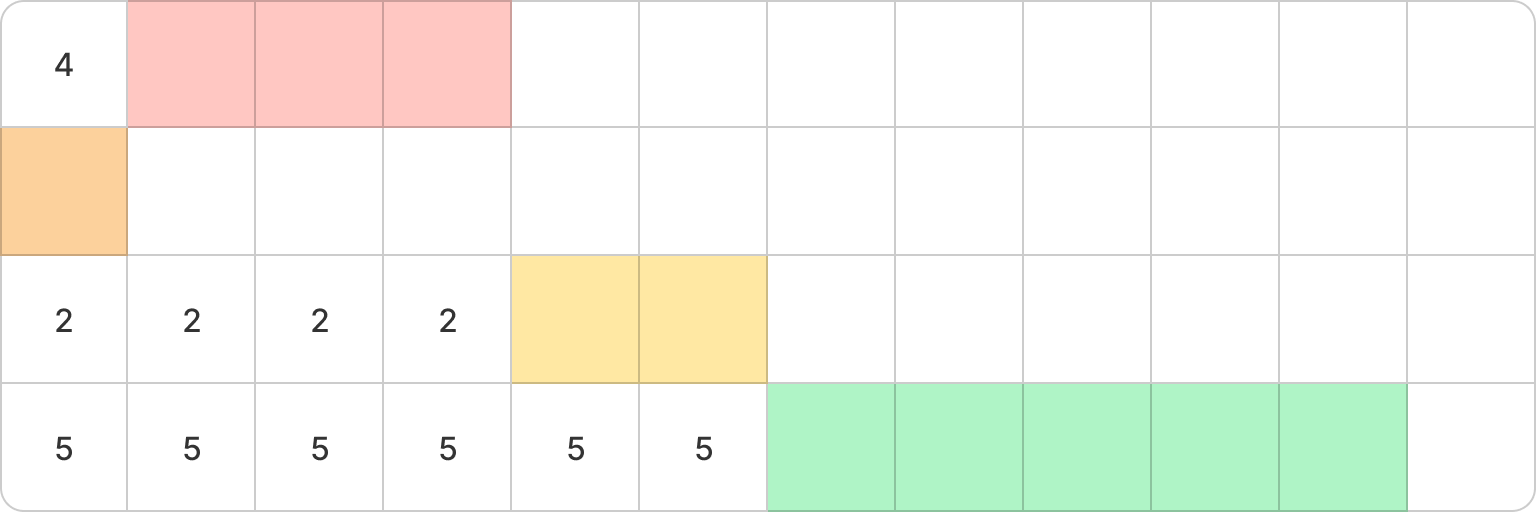
예를 들어, 입력이 위와 같을 때 보상금을 최대한 적게 주기 위해서는 위와 같은 형태가 된다.
이를 다르게 표현하여 보상금을 아낀다고 생각해 보자.
그렇다면 각 작업은 하루에 S/T만큼의 보상금을 아낄 수 있는 것이다.
이를 이용하여 S/T만큼의 점수를 얻는 문제로 바꾸어 보았을 때, S/T가 가장 큰 것부터 선택하는 것이 해당 문제에서의 해답이 된다.
예를 들어, 1234번 작업을 순서대로 진행했다고 가정해 보자.
그렇다면 S/T는 다음과 같다.
| 1 | 2 | 3 | 4 |
| 4/3 | 1000/1 | 2/2 | 5/5 |
1번과 2번의 순서를 맞바꾸지 않는다면 4/3원을 획득하지만, 1000/1원을 잃게 된다.
즉, 4/3원을 아낄 수 있지만 1000/1원을 보상금으로 지불해야 한다.
따라서, 1번과 2번의 순서를 바꾸어 1000/1원을 얻고 4/3원을 잃도록 해야 한다.
그렇기 때문에 S/T와 i번째 작업인 것을 기록하는 자료구조를 만들고 이를 S/T기준으로 내림차순 정렬한다면 정답을 구할 수 있다.
만약, S/T가 같다면 i를 기준으로 오름차순이 되도록 정렬해야 한다.
문제에서 답이 여러 개일 경우 오름차순으로 정렬된 해답을 원했기 때문이다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
struct Task
{
Task(int n, double c) : num(n), cost(c)
{};
int num;
double cost;
bool operator < (const Task& Other) const
{
if (cost == Other.cost) return num < Other.num;
return cost > Other.cost;
}
};
int N;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
vector<Task> tasks;
int size = 0;
for (int i = 1; i <= N; i++)
{
double t, s;
cin >> t >> s;
tasks.push_back({ i, s/t });
}
sort(tasks.begin(), tasks.end());
for (auto task : tasks)
{
cout << task.num << " ";
}
return 0;
}