문제 설명
2018년 강원도에서 새로운 동굴이 발견되었다. 이 동굴에는 총 N개의 넓은 방이 존재하며 좁은 통로로 서로 연결되어 있는 것으로 밝혀졌다. N개의 방은 1번부터 N번까지의 번호를 붙여 1번 방, 2번 방, …, N번 방으로 부른다. 통로는 정확히 N-1개가 발견되었는데, 각각 서로 다른 두 방 사이를 연결시켜 주며 중간에 다른 통로와 이어지는 경우는 없다고 한다. 또한 이 통로들을 이용하여 임의의 두 방 사이를 이동하는 것이 가능하며, 임의의 두 방 사이를 이동할 때 같은 통로를 두 번 이상 지나지 않는 경로는 유일한 것으로 밝혀졌다.
새로 발견된 동굴을 조사하기 위해 동굴 탐사 로봇 두 대를 이용하기로 하였다. 두 로봇은 어떤 시점이 되면 각자가 획득한 정보를 공유하기 위해 통신을 해야 한다. 두 로봇이 서로 통신을 하기 위해서는 동굴 내의 같은 통로 위에 위치해야만 한다. 참고로 임의의 통로의 양 끝에 위치한 두 방들도 그 통로 위에 위치해 있다고 간주한다.
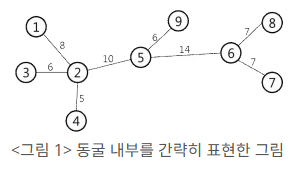
<그림 1>은 방이 9개인 동굴 내부를 간략하게 나타낸 예이다. <그림 1>에서 방은 원으로 표현되어 있으며 원 안의 수는 방 번호이다. 8개의 통로는 두 원 사이의 선분으로 표시되어 있으며 그 위의 정수 값이 통로의 길이이다. 예를 들어, 5번 방과 9번 방 사이에 길이가 6 인 통로가 있음을 알 수 있다. 만약 두 로봇이 1번 방과 9번 방에 위치해 있다면, 각각 2번 방과 5번 방으로 이동한 후 통신할 수 있으며 이때 이동한 거리의 합은 14로 최소이다.
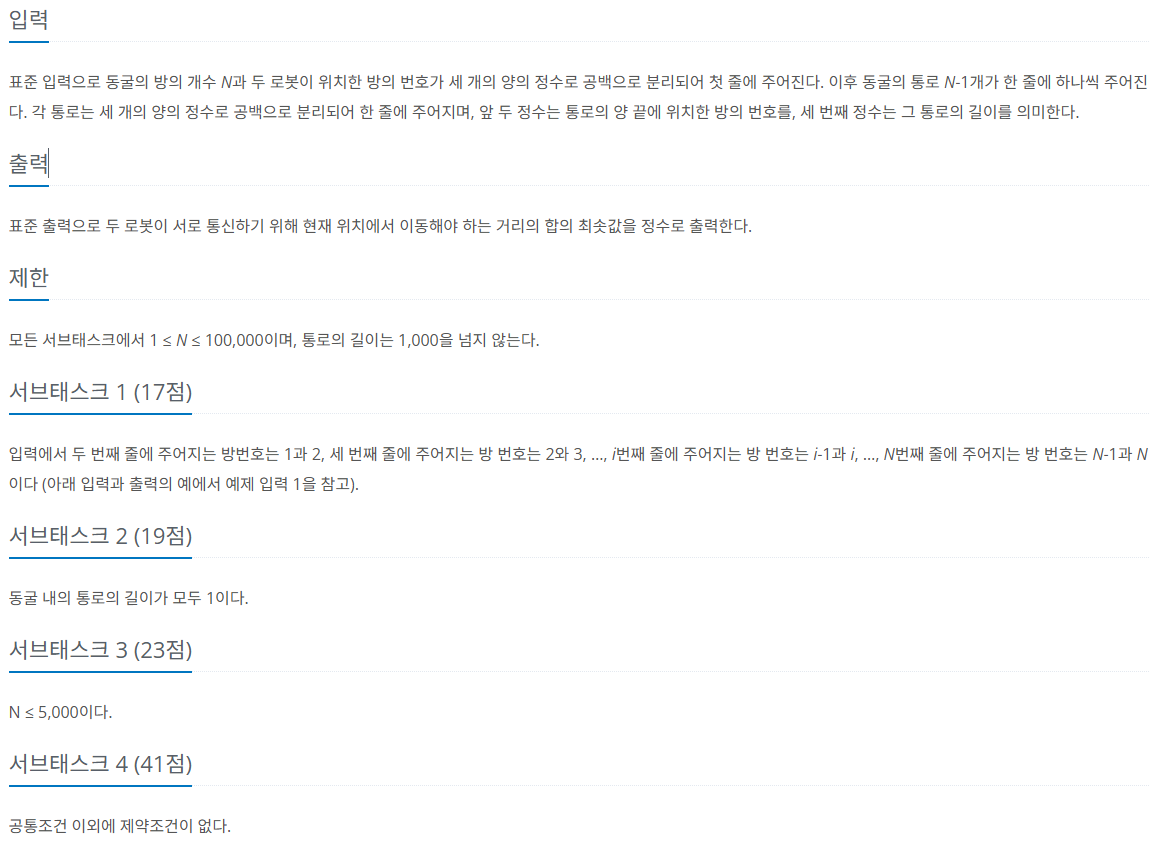
동굴 내의 통로에 대한 정보와 두 로봇의 현재 위치가 입력으로 주어질 때, 서로 통신하기 위해 이동해야 하는 거리의 합의 최솟값을 계산하는 프로그램을 작성하시오.
동굴의 각 통로는 양 끝에 위치한 두 방의 번호와 그 길이로 주어진다. 두 로봇의 위치는 방 번호로 주어진다.
https://www.acmicpc.net/problem/15971
제한 사항

풀이
문제를 요약하면, 두 로봇이 시작위치에서 하나의 통로를 사이에 두고 만날 경우 최소 이동거리를 구해야 한다.
문제의 조건이 트리 형식과 유사해서 최소 공통 조상을 찾는 문제로 바꿔보았다.
하지만, 이렇게 진행하게 되면 경로를 추적하는 게 쉽지 않아 다른 풀이를 생각해 봤다.
최소 공통 조상을 찾는다는 것은 두 노드 사이의 거리를 구하는 것과 같다.
즉, 두 로봇이 시작하는 노드끼리의 최소 거리를 구한다면 그 경로 중, 가장 긴 통로를 제거하면 정답이 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, S, E;
vector<bool> visited;
vector<vector<pair<int, int>>> roads;
int minDist = INT_MAX;
int ans = INT_MAX;
void dfs(int current, int total, int maxCost)
{
if (current == E)
{
minDist = min(minDist, total);
ans = min(ans, minDist - maxCost);
cout << ans;
exit(0);
}
for (auto& [next, cost] : roads[current])
{
if (visited[next]) continue;
visited[next] = true;
dfs(next, total + cost, max(maxCost, cost));
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> S >> E;
visited.resize(N + 1, false);
roads.resize(N+1);
for (int i = 0; i < N-1; i++)
{
int a, b, c;
cin >> a >> b >> c;
roads[a].push_back({ b,c });
roads[b].push_back({ a,c });
}
visited[S] = true;
dfs(S, 0, 0);
return 0;
}