문제 설명
1부터 34까지 수가 적힌 카드가 충분히 많이 있다. 이들 중 몇 장을 일렬로 늘어놓고, 그 숫자를 차례로 적었다. 예를 들어 아래와 같이 카드가 놓인 경우 숫자를 차례로 적으면 27123이 된다.
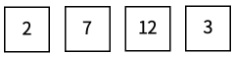
나중에, 적어 놓은 것에 맞게 다시 카드를 늘어놓으려고 보니, 방법이 여러 가지일 수 있다는 것을 알았다. 예를 들어 27123의 경우 아래와 같이 여섯 가지 다른 방법이 있다.
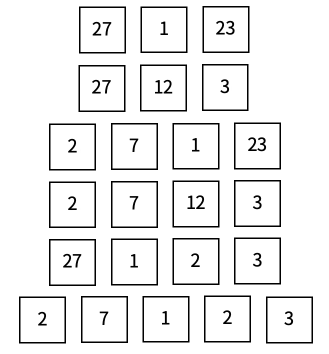
카드의 숫자를 차례로 적어 놓은 것이 주어질 때, 위와 같이 그것을 가지고 거꾸로 카드의 배열을 찾으려고 한다. 가능한 카드의 배열이 모두 몇 개인지 구하는 프로그램을 작성하시오.
제한 사항


풀이
문제를 요약하면, 1~34까지의 숫자카드를 이용해 주어진 문자열을 만들 수 있는 경우의 수를 세는 문제이다.
숫자 카드는 중복으로 사용이 가능하다.
해당 문제는 간단해 보이지만 함정이 하나 있다.
바로 0이다.
1~34 사이의 숫자 카드를 사용하기 때문에 0을 사용해서 문자열을 만들 수 없지만, 10이나 20, 30은 사용이 가능하다.
즉, 0은 무조건 두 자리 수로만 사용이 가능하다는 것이다.
문제를 간단히 만들어보면 현재 자리에서 한 자릿수를 고를 경우와 두 자릿수를 고를 경우를 고려하여 개수를 세면 된다.
개수를 세는 부분을 생각해보면 전체 경우의 수는 각 인덱스까지 만들 수 있는 경우의 수를 구했을 때 마지막 인덱스를 확인하면 된다.
즉, DP를 이용하면 효율적으로 문제를 풀 수 있다.
현재 인덱스까지 만들 수 있는 경우의 수는 다음과 같다.
- 현재 인덱스를 한 자리 수로 선택한 경우: 0이 아니라면 i-1까지 만든 경우의 수를 더해준다.
- 현재 인덱스를 두 자리 수로 선택한 경우: 선택한 수가 10~34 사이의 수라면 i-2까지 만든 경우의 수를 더해준다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
string num;
vector<int> dp;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> num;
dp.resize(num.length());
dp[0] = 1;
for (int i = 1; i < num.length(); i++)
{
if (num[i] != '0') dp[i] += dp[i - 1];
int n = stoi(num.substr(i - 1, 2));
if (10 <= n && n <= 34)
{
dp[i] += i - 2 >= 0 ? dp[i - 2] : 1;
}
}
cout << dp[num.length() - 1];
return 0;
}
문제 설명
1부터 34까지 수가 적힌 카드가 충분히 많이 있다. 이들 중 몇 장을 일렬로 늘어놓고, 그 숫자를 차례로 적었다. 예를 들어 아래와 같이 카드가 놓인 경우 숫자를 차례로 적으면 27123이 된다.

나중에, 적어 놓은 것에 맞게 다시 카드를 늘어놓으려고 보니, 방법이 여러 가지일 수 있다는 것을 알았다. 예를 들어 27123의 경우 아래와 같이 여섯 가지 다른 방법이 있다.

카드의 숫자를 차례로 적어 놓은 것이 주어질 때, 위와 같이 그것을 가지고 거꾸로 카드의 배열을 찾으려고 한다. 가능한 카드의 배열이 모두 몇 개인지 구하는 프로그램을 작성하시오.
제한 사항


풀이
문제를 요약하면, 1~34까지의 숫자카드를 이용해 주어진 문자열을 만들 수 있는 경우의 수를 세는 문제이다.
숫자 카드는 중복으로 사용이 가능하다.
해당 문제는 간단해 보이지만 함정이 하나 있다.
바로 0이다.
1~34 사이의 숫자 카드를 사용하기 때문에 0을 사용해서 문자열을 만들 수 없지만, 10이나 20, 30은 사용이 가능하다.
즉, 0은 무조건 두 자리 수로만 사용이 가능하다는 것이다.
문제를 간단히 만들어보면 현재 자리에서 한 자릿수를 고를 경우와 두 자릿수를 고를 경우를 고려하여 개수를 세면 된다.
개수를 세는 부분을 생각해보면 전체 경우의 수는 각 인덱스까지 만들 수 있는 경우의 수를 구했을 때 마지막 인덱스를 확인하면 된다.
즉, DP를 이용하면 효율적으로 문제를 풀 수 있다.
현재 인덱스까지 만들 수 있는 경우의 수는 다음과 같다.
- 현재 인덱스를 한 자리 수로 선택한 경우: 0이 아니라면 i-1까지 만든 경우의 수를 더해준다.
- 현재 인덱스를 두 자리 수로 선택한 경우: 선택한 수가 10~34 사이의 수라면 i-2까지 만든 경우의 수를 더해준다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
string num;
vector<int> dp;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> num;
dp.resize(num.length());
dp[0] = 1;
for (int i = 1; i < num.length(); i++)
{
if (num[i] != '0') dp[i] += dp[i - 1];
int n = stoi(num.substr(i - 1, 2));
if (10 <= n && n <= 34)
{
dp[i] += i - 2 >= 0 ? dp[i - 2] : 1;
}
}
cout << dp[num.length() - 1];
return 0;
}