문제 설명
트럭을 타고 이동하던 상근이는 경찰의 검문을 받게 되었다. 경찰은 상근이가 운반하던 화물을 하나하나 모두 확인할 것이기 때문에, 검문하는데 엄청나게 오랜 시간이 걸린다.
상근이는 시간을 때우기 위해서 수학 게임을 하기로 했다.
먼저 근처에 보이는 숫자 N개를 종이에 적는다. 그 다음, 종이에 적은 수를 M으로 나누었을 때, 나머지가 모두 같게 되는 M을 모두 찾으려고 한다. M은 1보다 커야 한다.
N개의 수가 주어졌을 때, 가능한 M을 모두 찾는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2981
제한 사항

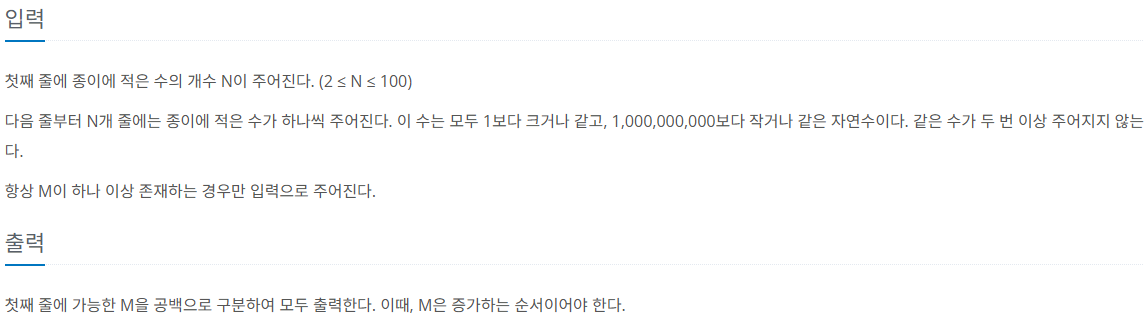
풀이
문제를 요약하면, N개의 수가 주어지고 이를 M으로 나눌 때 나머지가 모두 같아지는 M을 전부 구하는 것이다.
문제는 간단하지만 수학적인 지식이 없다면 문제를 풀지 못한다.
문제를 수식으로 전개한다면 쉽게 풀 수 있지만 수식을 만들어 내는 것이 쉽지 않다.
예시를 통해 수식을 만들어 보자.
3
6
34
38M과 공통된 나머지 r을 통해 수를 표현해 보자.
- 6 = a * M + r
- 34 = b * M + r
- 38 = c * M + r
우리가 알고 있는 수는 a, b, c, M, r 중 아무것도 없다.
하지만 식을 연립하여 미지수를 줄일 수 있다.
38 - 34 = (c - b) * M, 34 - 6 = (b - a) * M
→ 4 = (c - b) * M, 28 = (b - a) * M
이 식을 풀어보면 4와 28의 공약수가 M이 된다.
즉, 4와 28의 최대 공약수를 구한다면 최대 공약수의 약수들이 M이 될 수 있다.
최대 공약수는 재귀를 통해 간단하게 구할 수 있다.
a와 b(a > b)의 최대 공약수는 b와 a-b의 최대 공약수와 같다.
이는 유클리드 호제법으로 증명 되었다.
int GCD(int a, int b)
{
if (a < b) swap(a, b);
if (a % b == 0) return b;
return GCD(b, a - b);
}
최대 공약수를 구했다면 그 약수를 구하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
#define INPUT_OPTIMIZE cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define INF 2e9
using namespace std;
int N;
vector<int> nums;
int GCD(int a, int b)
{
if (a < b) swap(a, b);
if (a % b == 0) return b;
return GCD(b, a - b);
}
int main()
{
INPUT_OPTIMIZE;
cin >> N;
nums.resize(N);
for (int i = 0; i < N; i++)
{
cin >> nums[i];
}
sort(nums.begin(), nums.end(), greater<int>());
int gcd = nums[0] - nums[1];
for (int i = 1; i < N-1; i++)
{
gcd = GCD(gcd, nums[i] - nums[i + 1]);
}
vector<int> ans;
for (int i = 1; i * i <= gcd; i++)
{
if (gcd % i == 0)
{
if(i != 1) ans.push_back(i);
if (gcd / i != i) ans.push_back(gcd / i);
}
}
sort(ans.begin(), ans.end());
for (auto num : ans)
{
cout << num << " ";
}
return 0;
}
문제 설명
트럭을 타고 이동하던 상근이는 경찰의 검문을 받게 되었다. 경찰은 상근이가 운반하던 화물을 하나하나 모두 확인할 것이기 때문에, 검문하는데 엄청나게 오랜 시간이 걸린다.
상근이는 시간을 때우기 위해서 수학 게임을 하기로 했다.
먼저 근처에 보이는 숫자 N개를 종이에 적는다. 그 다음, 종이에 적은 수를 M으로 나누었을 때, 나머지가 모두 같게 되는 M을 모두 찾으려고 한다. M은 1보다 커야 한다.
N개의 수가 주어졌을 때, 가능한 M을 모두 찾는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2981
제한 사항


풀이
문제를 요약하면, N개의 수가 주어지고 이를 M으로 나눌 때 나머지가 모두 같아지는 M을 전부 구하는 것이다.
문제는 간단하지만 수학적인 지식이 없다면 문제를 풀지 못한다.
문제를 수식으로 전개한다면 쉽게 풀 수 있지만 수식을 만들어 내는 것이 쉽지 않다.
예시를 통해 수식을 만들어 보자.
3
6
34
38M과 공통된 나머지 r을 통해 수를 표현해 보자.
- 6 = a * M + r
- 34 = b * M + r
- 38 = c * M + r
우리가 알고 있는 수는 a, b, c, M, r 중 아무것도 없다.
하지만 식을 연립하여 미지수를 줄일 수 있다.
38 - 34 = (c - b) * M, 34 - 6 = (b - a) * M
→ 4 = (c - b) * M, 28 = (b - a) * M
이 식을 풀어보면 4와 28의 공약수가 M이 된다.
즉, 4와 28의 최대 공약수를 구한다면 최대 공약수의 약수들이 M이 될 수 있다.
최대 공약수는 재귀를 통해 간단하게 구할 수 있다.
a와 b(a > b)의 최대 공약수는 b와 a-b의 최대 공약수와 같다.
이는 유클리드 호제법으로 증명 되었다.
int GCD(int a, int b)
{
if (a < b) swap(a, b);
if (a % b == 0) return b;
return GCD(b, a - b);
}
최대 공약수를 구했다면 그 약수를 구하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
#define INPUT_OPTIMIZE cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define INF 2e9
using namespace std;
int N;
vector<int> nums;
int GCD(int a, int b)
{
if (a < b) swap(a, b);
if (a % b == 0) return b;
return GCD(b, a - b);
}
int main()
{
INPUT_OPTIMIZE;
cin >> N;
nums.resize(N);
for (int i = 0; i < N; i++)
{
cin >> nums[i];
}
sort(nums.begin(), nums.end(), greater<int>());
int gcd = nums[0] - nums[1];
for (int i = 1; i < N-1; i++)
{
gcd = GCD(gcd, nums[i] - nums[i + 1]);
}
vector<int> ans;
for (int i = 1; i * i <= gcd; i++)
{
if (gcd % i == 0)
{
if(i != 1) ans.push_back(i);
if (gcd / i != i) ans.push_back(gcd / i);
}
}
sort(ans.begin(), ans.end());
for (auto num : ans)
{
cout << num << " ";
}
return 0;
}