문제 설명
다솜이는 유료 고속도로를 가지고 있다. 다솜이는 현재 고속도로에 휴게소를 N개 가지고 있는데, 휴게소의 위치는 고속도로의 시작으로부터 얼만큼 떨어져 있는지로 주어진다. 다솜이는 지금 휴게소를 M개 더 세우려고 한다.
다솜이는 이미 휴게소가 있는 곳에 휴게소를 또 세울 수 없고, 고속도로의 끝에도 휴게소를 세울 수 없다. 휴게소는 정수 위치에만 세울 수 있다.
다솜이는 이 고속도로를 이용할 때, 모든 휴게소를 방문한다. 다솜이는 휴게소를 M개 더 지어서 휴게소가 없는 구간의 길이의 최댓값을 최소로 하려고 한다. (반드시 M개를 모두 지어야 한다.)
예를 들어, 고속도로의 길이가 1000이고, 현재 휴게소가 {200, 701, 800}에 있고, 휴게소를 1개 더 세우려고 한다고 해보자.
일단, 지금 이 고속도로를 타고 달릴 때, 휴게소가 없는 구간의 최댓값은 200~701구간인 501이다. 하지만, 새로운 휴게소를 451구간에 짓게 되면, 최대가 251이 되어서 최소가 된다.
https://www.acmicpc.net/problem/1477
제한 사항

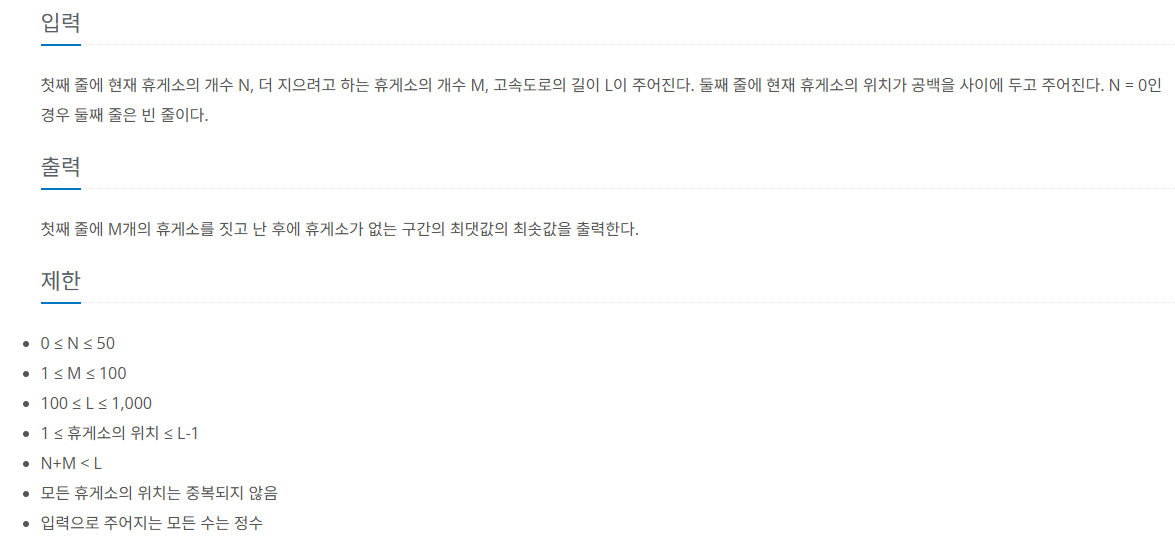
풀이
문제를 요약하면, 미리 설치되어 있는 N개의 휴게소에 추가로 M개의 휴게소를 지을 때 휴게소가 설치되지 않은 구간을 최소로 줄이는 것이다.
해당 문제는 이분 탐색으로 간단하게 풀 수 있다.
휴게소가 설치되지 않은 구간을 x라고 하면 N개의 휴게소를 살펴보며 x를 넘는 구간이 있다면 휴게소를 지어보면 된다.
그렇다면 그 구간을 x로 나눈 몫만큼 휴게소를 짓게 될 것이다.
예를 들어, 100만큼의 구간이 있고 x가 30이라고 한다면 총 3개의 휴게소를 추가로 지어야 한다.
단, x로 나누어 떨어지는 구간이라면 몫-1만큼만 지어도 된다.
90만큼의 구간에 30씩 떨어진 휴게소를 짓는다면 2개만 지어도 각 휴게소의 구간은 30이 되기 때문이다.
이러한 조건을 통해 가능한 x의 범위를 이분 탐색으로 정해나가면 된다.
x의 범위의 초깃값은 최소 1, 최대 L이 될 것이다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
#define INPUT_OPTIMIZE cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define INF 2e9
using namespace std;
int N, M, L;
vector<int> areas;
bool Check(int len)
{
int cnt = 0;
for (int i = 1; i < N + 2; i++)
{
int gap = areas[i] - areas[i - 1];
if (gap % len == 0)
{
cnt += gap / len - 1;
}
else
{
cnt += gap / len;
}
}
return cnt <= M;
}
int main()
{
INPUT_OPTIMIZE;
cin >> N >> M >> L;
areas.resize(N + 2);
int left = 1;
int right = L;
areas[0] = 0;
areas[N + 1] = L;
for (int i = 0; i < N; i++)
{
cin >> areas[i];
if (i == 0) continue;
}
sort(areas.begin(), areas.end());
int ans = right;
while(left <= right)
{
int mid = (left + right) / 2;
if (Check(mid))
{
right = mid - 1;
ans = min(ans, mid);
}
else
{
left = mid + 1;
}
}
cout << ans;
return 0;
}
