백준 10216 - Count Circle Groups

문제 설명

백준이는 국방의 의무를 수행하기 위해 떠났다. 혹독한 훈련을 무사히 마치고 나서, 정말 잘 생겼고 코딩도 잘하는 백준은 그 특기를 살려 적군의 진영을 수학적으로 분석하는 일을 맡게 되었다.

2차원 평면 위의 N곳에 적군의 진영이 설치되어 있다. 각 적군의 진영들은 진영마다 하나의 통신탑을 설치해, i번째 적군의 통신탑은 설치 위치로부터 Ri 이내 거리에 포함되는 모든 지역을 자신의 통신영역 Ai로 가지게 된다. 만약 임의의 통신영역 Ai와 Aj가 닿거나 겹치는 부분이 있다면 진영 i와 진영 j는 직접적으로 통신이 가능하다. 물론 직접적으로 통신이 가능하지 않더라도, 임의의 지역 i와 j가 중간에 몇 개의 직접통신을 거쳐서 최종적으로 통신이 가능하다면 i와 j는 상호간에 통신이 가능한 것으로 본다.

적들은 영리해서, 상호간에 통신이 가능한 부대끼리는 결집력있는 한 그룹처럼 행동한

https://www.acmicpc.net/problem/10216

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면 N개의 타워 위치와 범위가 주어지고 그 범위끼리 닿아있는 타워는 하나의 그룹으로 묶을 수 있다.

모든 타워를 그룹으로 묶는다면 몇 개의 그룹이 생기는지 구하는 것이다.

 

해당 문제는 두 가지 문제로 분리할 수 있다.

• 타워끼리 범위가 겹치는지 확인
• 범위가 겹치는 타워를 그룹으로 묶기

 

우선 타워끼리 범위가 겹치는지 확인하는 방법은 두 원이 충돌하는지 판정하는 법과 동일하다.

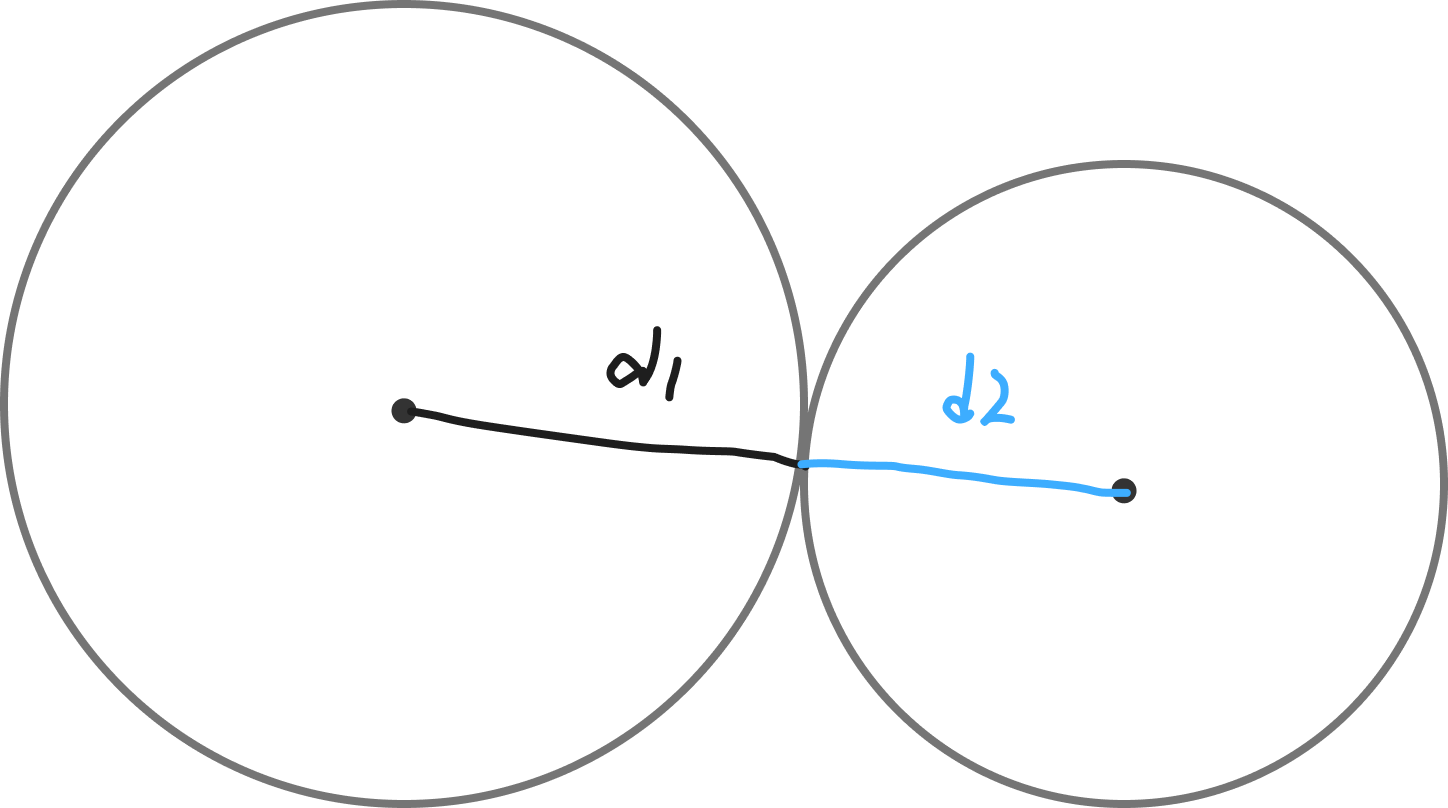
두 원이 충돌하려면 위 그림처럼 두 원의 중심사이의 거리가 d1 + d2보다 작거나 같아야 한다.

따라서 다음과 같은 식을 통해 두 원이 충돌하는지 확인할 수 있다.

float dist = sqrt(abs(y2 - y1) * abs(y2 - y1) + abs(x2 - x1) * abs(x2 - x1));

if (dist <= d1 + d2)
{
	//충돌
}

 

그럼 이제 원들끼리 그룹을 지으면 된다.

그룹을 만드는 방법은 여러 가지가 있지만 가장 먼저 생각난 것은 BFS였다.

임의의 원을 시작으로 방문하지 않은 원 중 충돌하는 원을 모두 구한다.

충돌하는 원을 큐에 다시 넣어 이를 반복하면 하나의 그룹이 완성된다.

그룹에 포함되지 않은 원을 시작으로 위의 과정을 반복하면 전체 그룹의 개수를 알 수 있다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>
#include <unordered_set>
using namespace std;
#define INPUT_OPTIMIZE cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define INF 2e9

using namespace std;
int T, N;
vector<tuple<int, int, int>> towers;
vector<bool> visited;

int main()
{
	INPUT_OPTIMIZE;

	cin >> T;

	while (T--)
	{
		cin >> N;

		towers.clear();
		visited.clear();
		visited.resize(N, false);

		for (int i = 0; i < N; i++)
		{
			int x, y, d;
			cin >> x >> y >> d;
			towers.push_back({ x,y,d });
		}

		int ans = 0;
		for (int i = 0; i < N; i++)
		{
			if (visited[i]) continue;
			ans++;

			queue<int> q;
			q.push(i);

			while (!q.empty())
			{
				int idx = q.front();
				q.pop();

				if (visited[idx]) continue;
				visited[idx] = true;

				auto& [y1, x1, d1] = towers[idx];
				for (int j = 0; j < N; j++)
				{
					if (visited[j]) continue;

					auto& [y2, x2, d2] = towers[j];
					float dist = sqrt(abs(y2 - y1) * abs(y2 - y1) + abs(x2 - x1) * abs(x2 - x1));

					if (dist <= d1 + d2)
					{
						q.push(j);
					}
				}
			}
		}

		cout << ans << "\n";
	}

	return 0;
}

---

 

 

 

 

 

추가

그룹을 묶는 방법을 유니온 파인드로 변경하면 큐에 들어간 타워마다 모든 타워를 살펴보는 과정을 $N^2$로 줄일 수 있어서 시간을 많이 단축할 수 있다.

---