프로그래머스[Lv.3] - 스티커 모으기(2)

 

 

문제 설명

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

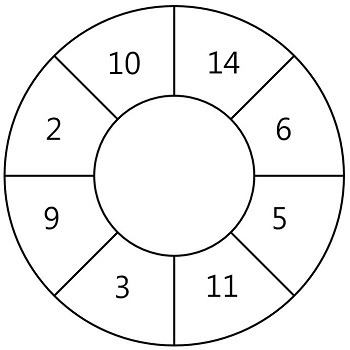
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

---

 

 

 

 

 

 

제한 사항

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

---

 

 

 

 

 

 

풀이

문제를 요약하면 그림같이 원형으로 배치된 스티커를 적절하게 뜯어 적힌 점수의 최댓값을 구하면 된다.

단, 인접한 스티커를 연속해서 뜯을 수 없다.

 

일단 문제를 간단하게 만들어 보면 풀이 방법을 쉽게 찾을 수 있다.

문제는 원형 스티커이지만 이를 일자로 폈다고 생각을 해보자.

[14, 6, 5, 11, 3, 9, 2, 10]

만약 1번(14) 스티커를 뜯었다고 해보자.

그렇다면 2번(6) 스티커는 뜯을 수 없다.

이러한 규칙을 적용해서 쭉 진행하면서 얻을 수 있는 점수의 최댓값을 기록한다고 해보자.

14	6	5	11	3	9	2	10
14	14	19	25	22	34	34	?

바로 인접한 스티커를 뗄 수 없기 때문에 i번째 스티커를 뜯을 때 얻을 수 있는 최댓값은 다음과 같다.

dp[i] = Math.Max(dp[i-1], dp[i-2] + sticker[i]);

그리고 이제 마지막 최댓값의 ?로 처리한 이유만 해결하면 된다.

마지막을 ?로 기록한 이유는 아까 제외한 원형이라는 요소 때문이다.

현재 dp에 기록한 내용은 1번 스티커를 뜯었을 때 상황이다.

1번 스티커를 뜯었기 때문에 마지막 스티커는 뜯지 못한다.

따라서 dp의 마지막에 기록될 값은 다음과 같다.

dp[N-1] = dp[N-2]; // 34

 

여기서 끝이 아니다.

1번 스티커를 뜯지 않고 진행할 수 있다.

따라서 이런 경우까지 동일한 방법으로 처리하면 정답을 얻을 수 있다.

이때는 마지막 스티커를 뜯을 수 있다.

// 0번을 안뜯을 때
dp[1] = sticker[1];
for(int i = 2; i < N; i++)
{
    dp[i] = Math.Max(dp[i-1], dp[i-2] + sticker[i]);
}

 

마지막으로 1번을 뜯을 때와 뜯지 않았을 때 중 최댓값을 고르면 된다.

---

 

 

 

 

 

전체 코드

using System;
using System.Linq;
using System.Collections.Generic;

class Solution
{
    public int solution(int[] sticker)
    {
        if(sticker.Length == 1)
        {
            return sticker[0];
        }
        
        int answer = 0;
        
        int N = sticker.Length;
        int[,] dp = new int[2, N];
        
        // 0번을 뜯을 때
        dp[0, 0] = sticker[0];
        dp[0, 1] = Math.Max(dp[0, 0], sticker[1]);
        for(int i = 2; i < N - 1; i++)
        {
            dp[0, i] = Math.Max(dp[0, i-1], dp[0, i-2] + sticker[i]);
        }
        dp[0, N-1] = dp[0, N-2];
        
        // 0번을 안뜯을 때
        dp[1, 1] = sticker[1];
        for(int i = 2; i < N; i++)
        {
            dp[1, i] = Math.Max(dp[1, i-1], dp[1, i-2] + sticker[i]);
        }
        
        answer = Math.Max(dp[0, N-1], dp[1, N-1]);

        return answer;
    }
}

---