규제 적용
로지스틱 회귀에 규제를 적용해보자.
앞에서 만들어 놓은 SingleLayer 클래스에 L1 규제와 L2 규제를 적용하자.
def __init__(self):
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.w_history =[]
self.lr = learning_rate
self.l1 = l1
self.l2 = l2l1, l2 변수를 만들었다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.w = np.ones(x.shape[1]) #가중치 초기화
self.b = 0 #절편 초기화
self.w_history.append(self.w.copy()) #가중치 기록
np.random.seed(2)
for i in range(epochs):
loss = 0
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes:
z = self.forpass(x[i]) #정방향 계산
a = self.activation(z) #활성화 함수 적용
err = -(y[i] - a) #오차 계산
w_grad, b_grad = self.backprop(x[i], err) #역방향 계산
w_grad += self.l1 * np.sign(self.w) + self.l2 * self.w #규제 적용
self.w -= self.lr * w_grad
self.b -= b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10,1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a))
self.losses.append(loss/len(y) + self.reg_loss()) #평균 손실 조장
self.update_val_loss(x_val, y_val) #검증 세트 손실 계산
def reg_loss(self):
return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)
검증 세트의 손실을 계산하는 update_val_loss() 메서드도 변경하자.
def update_val_loss(self, x_val, y_val):
if x_val is None:
return
val_loss = 0
for i in range(len(x_val)):
z = self.forpass(x_val[i]) #정방향 계산
a = self.activation(z) #활성화 함수 적용
a = np.clip(a, 1e-10,1-1e-10)
val_loss += -(y_val[i]*np.log(a) + (1-y_val[i])*np.log(1-a))
slef.val_losses.append(val_loss/len(y_val) + self.reg_loss())
L1 규제 적용
L1 규제의 강도를 0.0001, 0.001, 0.01 세가지로 훈련을 해보자

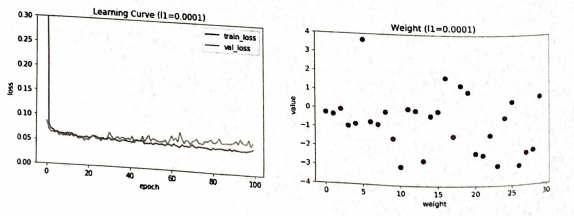
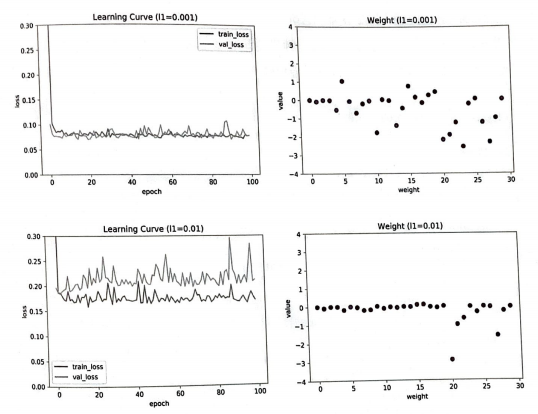
학습 곡선 그래프를 보면 규제가 더 커질수록 훈련 세트의 손실과 검증 세트의 손실이 모두 높아진다.
즉, 과소적합 현상이 나타난다.
L1 값이 커질수록 가중치의 값이 0에 가까워진다.
가장 적절한 l1은 0.001 정도인 것 같다.
L2 규제 적용
L2 규제도 0.0001, 0.001, 0.01을 적용해 보자.

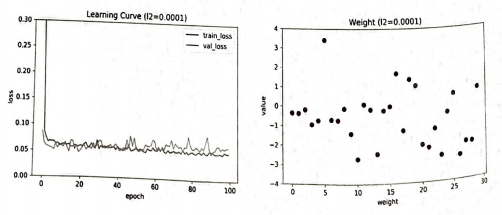
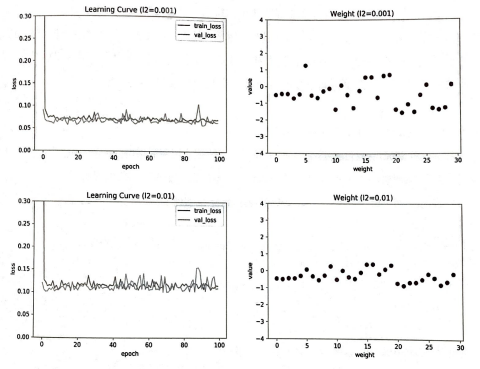
L2 규제도 L1 규제와 비슷한 양상을 보인다.
L2 규제는 규제 강도가 강해져도 L1 규제만큼 과소 적합이 심해지지는 않는다.
가중치도 0에 너무 가까게 줄어들지 않는다.
