다중 분류
다중 분류 신경망을 만들기 위해서는 소프트맥스(softmax) 함수와 크로스 엔트로피(cross-entropy) 손실 함수라는 새로운 개념을 알아야 한다.
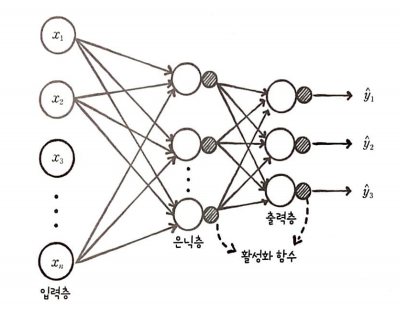
이진 분류와 다중 분류는 크게 다르지 않다.
출력층의 개수만 다르고 나머지는 동일하다. 이진 분류는 양성 클래스에 대한 확률 하나만 출력하고 다중 분류는 각 클래스에 대한 확률 값을 출력한다.
예를 들어 첫 번째 클래스에 대한 확률값이 y1, 두 번째 클래스에 대한 확률값은 y2, 세 번째 클래스에 대한 확률값은 y3로 출력된다.
다중 분류 긴경망은 출력층에 분류할 클래스 개수만큼 뉴런을 배치해야 한다.
다중 분류의 문제점과 소프트맥스 함수
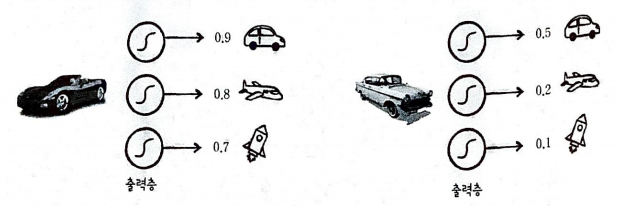
숫자는 확률을 얘기한다. 0.9는 90%이다.
왼쪽과 오른쪽의 신경망 모두 자동차를 타깃 클래스로 예측하고 있다.
하지만, 왼쪽과 오른쪽의 활성화 값은 차이가 있다. 왼쪽은 모든 클래스에 대해서 높은 값을 가지지만, 오른쪽은 자동차 클래스에 대해서만 비교적 높은 값을 가진다.
- 활성화 출력의 합이 1이 아니면 비교하기 어렵다.
확률 값이 높기만 해서는 올바른 예측을 하기 쉽지 않다. 왼쪽을 보면 세 클래스 모두 높은 확률로 맞다고 하는
꼴이다. - 소프트맥스 함수 적용해 출력 강도를 정규화한다.
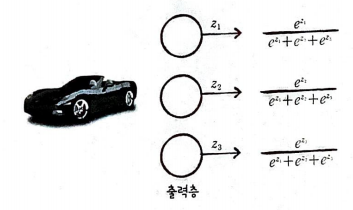
출력층의 출력 강도를 정규화하는 소프트맥스 함수(softmax function)를 사용하면 위 문제를 쉽게 해결할 수 있다.
출력 강도를 정규화한다는 의미는 전체 출력값의 합을 1로 만든다는 의미이다. 만약 출력이 3개라면 식은
다음과 같다.
시그모이드 함수 공식은 다음과 같다.
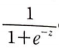
이를 z에 대해 정리하면 다음 식을 얻을 수 있다.
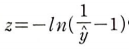
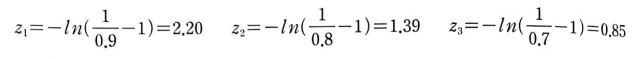
이 값을 소프트맥스 함수에 대입하면 다음과 같은 정규화된 값을 얻을 수 있다.
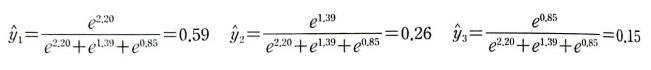
정규화를 하여 자동차 59%, 비행기 26%, 로켓 15%가 되었다.
다중 분류에서 출력층을 통과한 값들은 소프트맥스 함수를 거치며 적절한 확률값으로 변한다.
크로스 엔트로피 손실 함수
크로스 엔트로피 손실 함수를 소개할 때 '로지스틱 손실 함수를 일반화했다'라고 한다.
로지스틱 손실 함수가 크로스 엔트로피 손실 함수의 이진 분류 버전이기 때문이다.

크로스 엔트로피 손실 함수의 시그마 기호 위의 값(c)은 전체 클래스 개수를 의미한다.
타깃과 활성화 출력의 로그값을 곱하여 더한 것이다.
정답은 1, 나머지는 0이라 나머지 클래스의 값들은 0이 된다. 앞에 예시를 적용해보면 다음과 같다.
-(1*0.59 + 0*0.26 + 0*0.15)이다. 따라서 다음과 같은 식이 도출된다.
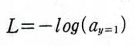
이제 크로스 엔트로피 손실 함수를 미분해보자.
3개의 클래스를 가진 다중 분류의 예를 들어 크로스 엔트로피 손실 함수의 미분 과정을 알아보자.
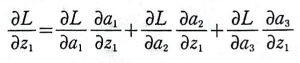
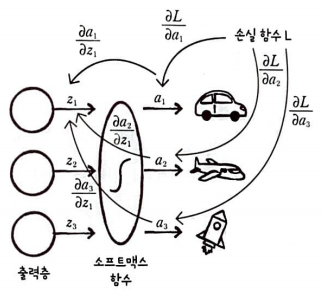
a1, a2, a3가 모두 z1의 함수이고 손실 함수 L이 a1, a2, a3의 함수이다.
먼저 L을 a1에 대하여 미분해보자.
L = -(y1*log(a1) + y2*log(a2) + y3*log(a3))이다.
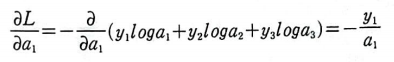
a1에 대한 함수만 취급하여 편미분을 진행하기 때문에 다음과 같은 결과가 나온다.
마찬가지로 a2, a3에 대해 미분해보자.
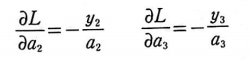
이제 L을 z1에 대해 미분한 식은 다음과 같이 쓸 수 있다.
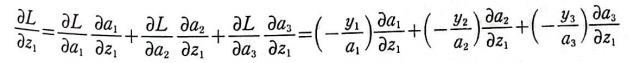
a를 z에 대해 미분한 식만 알면 최종 식을 구할 수 있다.
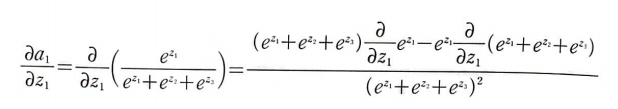
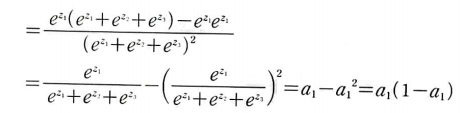
a2, a3도 동일하게 진행하자.
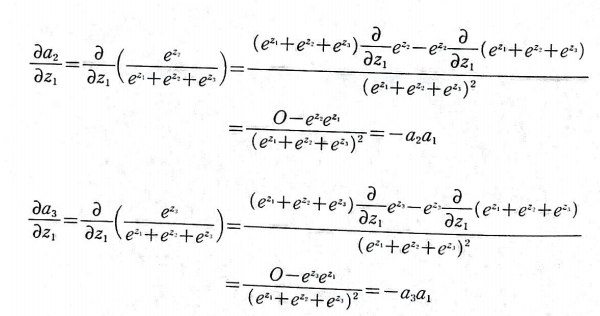
이제 총 식을 정리하면 다음과 같다.
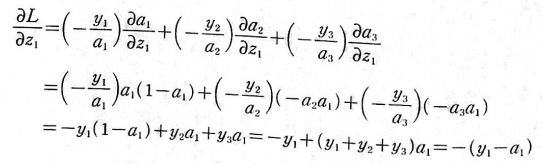
y1+y2+y3는 타깃의 합인데, 분류 문제에서 타깃의 합은 정답 타깃이 1이고 나머지는 0이므로 항상 1이다.
즉, 최종적으로 다음과 같다.
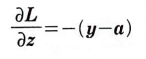
로지스틱 손실 함수의 미분과 정확히 일치한다.
다중 분류
다중 분류 신경망을 만들기 위해서는 소프트맥스(softmax) 함수와 크로스 엔트로피(cross-entropy) 손실 함수라는 새로운 개념을 알아야 한다.

이진 분류와 다중 분류는 크게 다르지 않다.
출력층의 개수만 다르고 나머지는 동일하다. 이진 분류는 양성 클래스에 대한 확률 하나만 출력하고 다중 분류는 각 클래스에 대한 확률 값을 출력한다.
예를 들어 첫 번째 클래스에 대한 확률값이 y1, 두 번째 클래스에 대한 확률값은 y2, 세 번째 클래스에 대한 확률값은 y3로 출력된다.
다중 분류 긴경망은 출력층에 분류할 클래스 개수만큼 뉴런을 배치해야 한다.
다중 분류의 문제점과 소프트맥스 함수

숫자는 확률을 얘기한다. 0.9는 90%이다.
왼쪽과 오른쪽의 신경망 모두 자동차를 타깃 클래스로 예측하고 있다.
하지만, 왼쪽과 오른쪽의 활성화 값은 차이가 있다. 왼쪽은 모든 클래스에 대해서 높은 값을 가지지만, 오른쪽은 자동차 클래스에 대해서만 비교적 높은 값을 가진다.
- 활성화 출력의 합이 1이 아니면 비교하기 어렵다.
확률 값이 높기만 해서는 올바른 예측을 하기 쉽지 않다. 왼쪽을 보면 세 클래스 모두 높은 확률로 맞다고 하는
꼴이다. - 소프트맥스 함수 적용해 출력 강도를 정규화한다.
출력층의 출력 강도를 정규화하는 소프트맥스 함수(softmax function)를 사용하면 위 문제를 쉽게 해결할 수 있다.
출력 강도를 정규화한다는 의미는 전체 출력값의 합을 1로 만든다는 의미이다. 만약 출력이 3개라면 식은
다음과 같다.

시그모이드 함수 공식은 다음과 같다.
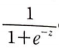
이를 z에 대해 정리하면 다음 식을 얻을 수 있다.
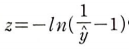
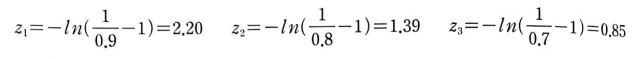
이 값을 소프트맥스 함수에 대입하면 다음과 같은 정규화된 값을 얻을 수 있다.
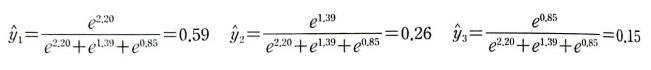
정규화를 하여 자동차 59%, 비행기 26%, 로켓 15%가 되었다.
다중 분류에서 출력층을 통과한 값들은 소프트맥스 함수를 거치며 적절한 확률값으로 변한다.
크로스 엔트로피 손실 함수
크로스 엔트로피 손실 함수를 소개할 때 '로지스틱 손실 함수를 일반화했다'라고 한다.
로지스틱 손실 함수가 크로스 엔트로피 손실 함수의 이진 분류 버전이기 때문이다.

크로스 엔트로피 손실 함수의 시그마 기호 위의 값(c)은 전체 클래스 개수를 의미한다.
타깃과 활성화 출력의 로그값을 곱하여 더한 것이다.
정답은 1, 나머지는 0이라 나머지 클래스의 값들은 0이 된다. 앞에 예시를 적용해보면 다음과 같다.
-(1*0.59 + 0*0.26 + 0*0.15)이다. 따라서 다음과 같은 식이 도출된다.
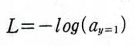
이제 크로스 엔트로피 손실 함수를 미분해보자.
3개의 클래스를 가진 다중 분류의 예를 들어 크로스 엔트로피 손실 함수의 미분 과정을 알아보자.
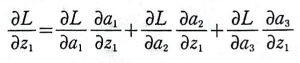

a1, a2, a3가 모두 z1의 함수이고 손실 함수 L이 a1, a2, a3의 함수이다.
먼저 L을 a1에 대하여 미분해보자.
L = -(y1*log(a1) + y2*log(a2) + y3*log(a3))이다.
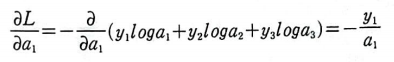
a1에 대한 함수만 취급하여 편미분을 진행하기 때문에 다음과 같은 결과가 나온다.
마찬가지로 a2, a3에 대해 미분해보자.
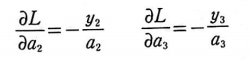
이제 L을 z1에 대해 미분한 식은 다음과 같이 쓸 수 있다.
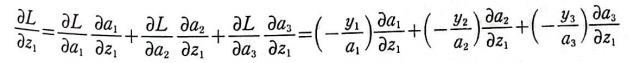
a를 z에 대해 미분한 식만 알면 최종 식을 구할 수 있다.
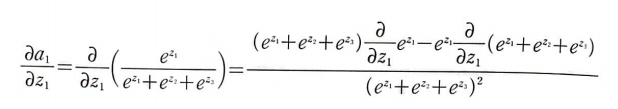
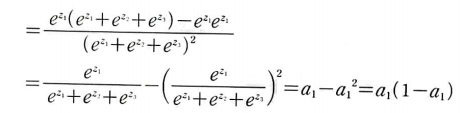
a2, a3도 동일하게 진행하자.
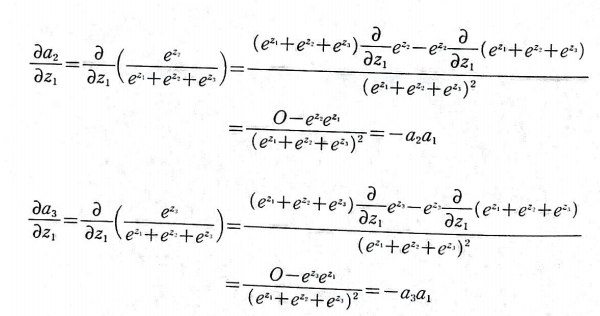
이제 총 식을 정리하면 다음과 같다.
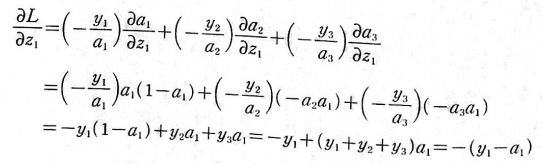
y1+y2+y3는 타깃의 합인데, 분류 문제에서 타깃의 합은 정답 타깃이 1이고 나머지는 0이므로 항상 1이다.
즉, 최종적으로 다음과 같다.
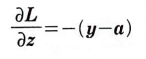
로지스틱 손실 함수의 미분과 정확히 일치한다.
