케라스 합성곱 신경망 만들기
케라스의 합성곱층은 Conv2D 클래스이다. 최대 풀링은 MaxPooling2D 클래스를 사용하고, 특성 맵을 일렬로 펼칠 때는 Flatten 클래스를 사용한다.
from tensorflow.keras.layers import Conv2D, MaxPolling2D, Flatten, Dense필요한 클래스를 임포트한다.
합성곱층 쌓기
합성곱층을 추가한다. Conv2D 클래스의 첫 번째 매개변수는 합성곱 커널의 개수이다.
두 번째 매개변수는 합성곱 커널의 크기로 높이와 너비를 튜플로 전달한다.
합성곱 커널로는 전형적으로 3 x 3 또는 5 x 5 크기를 많이 사용한다. activation 매개변수에 렐루 활성화 함수를 지정한다. 패딩은 세임 패딩을 사용하는데, tf.nn.con2d() 함수와는 달리 패딩 매개변수는 대소문자를 구분하지 않는다.
Sequential 클래스에 층을 처음 추가할 때는 배치 차원을 제외한 입력의 크기를 지정한다.
conv1 = tf.keras.Sequential()
conv1.add(Conv2D(10, (3, 3), activation='relu', padding='same', input_shape=(28,28,1)))
풀링층 쌓기
풀링층을 추가한다. MaxPooling2D 클래스의 첫 번째 매개변수는 풀링의 높이와 너비를 나타내는 튜플이며, 스트라이드는 strides 매개변수에 지정할 수 있다. 이 매개변수의 기본값은 풀링의 크기이다.
패딩은 padding 매개변수에 지정하며 기본값은 'valid'이다.
conv1.add(MaxPooling2D((2, 2)))
완전 연결층에 주입할 수 있도록 특성 맵 펼치기
풀링 다음에는 완전 연결층에 연결하기 위해 배치 차원을 제외하고 일렬로 펼쳐야 한다.
conv1.add(Flatten())
완전 연결층 쌓기
마지막으로 완전 연결층을 추가한다. 첫 번째 완전 연결층에는 100개의 뉴런을 사용하고 렐루 활성화 함수를 적용한다.
마지막 출력층에는 10개의 클래스에 대응하는 10개의 뉴런을 사용하고 소프트맥스 활성화 함수를 적용한다.
conv1.add(Dense(100, activation='relu'))
conv1.add(Dense(10, activation='softmax'))모델 구조 살펴보기
케라스를 사용하여 합성곱 신경망을 아주 간단하게 만들었다.
모델의 summary() 메서드를 사용하면 conv1 모델의 구조를 자세히 조사할 수 있다.
conv1.summary()
출력 결과를 보면 합성곱층(Conv2D)의 출력 크기는 배치 차원을 제외하고 28 x 28 x 10이다.
이때 배치 차원이 None인 이유는 배치 입력의 개수는 훈련할 때 전달되는 샘플 개수에 따라 달라지기 때문이다.
합성곱 커널은 10개를 사용했으므로 마지막 차원이 10이다.
모델 파라미터의 개수는 전체 가중치의 크기와 커널마다 하나씩 절편을 추가하면 3 x 3 x 1 x 10 + 10 = 100이다.
풀링층과 특성 맵을 완전 연결층에 펼쳐서 주입하기 위해 추가한 Flatten 층에는 가중치가 없다.
첫 번째 완전 연결층에는 1960개(14 x 14 x 10)의 입력이 100개의 뉴런에 연결된다.
가중치는 뉴런마다 하나씩 있으므로 첫 번째 완전 연결층의 가중치 개수는 196100(1960 x 100 + 100) 개다.
마찬가지로 두 번째 완전 연결층의 가중치 개수는 1010(100 x 10 + 10) 개다.
가중치의 개수를 보면 완전 연결층에 비해 합성곱층의 가중치 개수가 아주 적다.
그래서 합성곱층을 여러 개 추가해도 학습할 모델 파라미터의 개수가 크게 늘지 않아서 계산 효율성이 좋다.
합성곱 신경망 모델 훈련
metrics 매개변수에 'accuracy'를 전달하여 훈련시켜 보자.
conv1.compile(optimizer='adam', loss='categorical_crossentropy',metrics=['accuracy'])최적화 알고리즘으로 기본 경사 하강법만 사용했었다. 이번에는 적응적 학습률 알고리즘 중 하나인 아담(Adam) 옵티마이저를 사용한다. 아담은 Adaptive Moment Estimation을 줄여 만든 이름이다.
아담은 손실 함수의 값이 최적값에 가까워질수록 학습률을 낮춰 손실 함수의 값이 안정적으로 수렴될 수 있게 해 준다.
ConvolutionNetwork 클래스로 수행했던 것과 동일하게 20번의 에포크 동안 훈련해 보자.
history = conv1.fit(x_train, y_train_encoded, epochs=20, validation_data=(x_val, y_val_encoded))plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()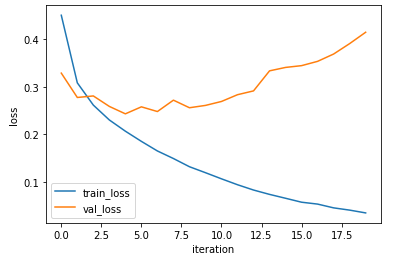
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('iteration')
plt.legend(['train_accuracy', 'val_accuracy'])
plt.show()
검증 세트 정확도가 92%까지 크게 증가했다.
하지만 정확도와 손실을 그래프로 그려보니 몇 번의 에포크 만에 검증 손실이 크게 증가했다.
이는 과대 적합이 일찍 발생했음을 의미한다.
드롭아웃
신경망에서 과대 적합을 줄이는 방법 중 하나는 드롭아웃이다.
드롭아웃은 무작위로 일부 뉴런을 비활성화시킨다. 무작위로 일부 뉴런을 비활성화시키면 특정 뉴런에 과도하게 의존하여 훈련하는 것을 막아준다.
예를 들면 다음과 같다.
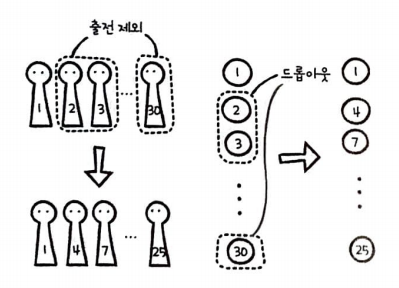
만약 2, 3, 30번이 핵심이던 팀에서 2, 3, 30번을 경기에서 제외시킨다면 전력이 크게 감소할 것이다.
따라서 다른 선수들도 고르게 훈련시켜 전력 손실을 최소화해야 한다.
일부 뉴런이 비활성화되었을 때에도 타깃을 잘 예측하려면 특정 뉴런에 과도하게 의존하지 않고 모든 뉴런이 의미 있는 패턴을 학습해야 한다. 뉴런이 훈련 세트에 있는 패턴을 고르게 감지하므로 전체적인 일반화 성능이 높아진다.
드롭아웃은 모델을 학습할 때만 적용한다.
상대적으로 테스트와 실전의 출력값이 훈련할 때의 출력값보다 높아지므로 테스트나 실전에서는 출력값을 드롭아웃 비율만큼 낮춰야 한다.
텐서플로에서는 드롭아웃의 비율만큼 뉴런의 출력을 높인다.
출력값을 드롭아웃 비율만큼 낮춰야 한다. 그런데 텐서플로를 비롯하여 대부분의 딥러닝 프레임워크는 반대로 이 문제를 해결한다.
즉, 훈련할 때 드롭아웃 비율만큼 뉴런의 출력을 높여 훈련시킨다.
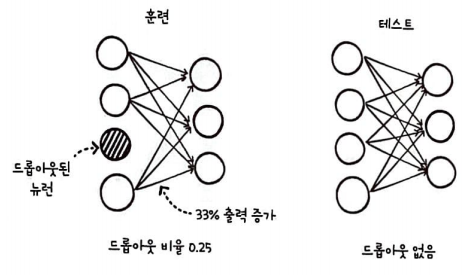
드롭아웃의 비율이 0.25(25%)이므로 출력을 33% 정도 증가시킨다. ( 1 / (1 - 0.25) = 1.333...)
실전에서는 드롭아웃되는 뉴런이 없기 때문에 출력을 증가시키지 않는다.
드롭아웃 추가된 모델
conv2 = tf.keras.Sequential()
conv2.add(Conv2D(10, (3, 3), activation='relu', padding='same', input_shape=(28, 28, 1)))
conv2.add(MaxPooling2D((2, 2)))
conv2.add(Flatten())
conv2.add(Dropout(0.5))
conv2.add(Dense(100, activation='relu'))
conv2.add(Dense(10, activation='softmax'))
conv2.summary()
훈련
conv2.compile(optimizer='adam', loss='categorical_crossentropy',metrics=['accuracy'])
history = conv2.fit(x_train, y_train_encoded, epochs=20, validation_data=(x_val, y_val_encoded))plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()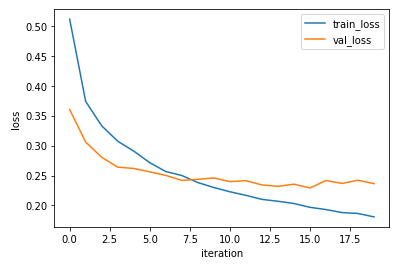
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('iteration')
plt.legend(['train_accuracy', 'val_accuracy'])
plt.show()
케라스 합성곱 신경망 만들기
케라스의 합성곱층은 Conv2D 클래스이다. 최대 풀링은 MaxPooling2D 클래스를 사용하고, 특성 맵을 일렬로 펼칠 때는 Flatten 클래스를 사용한다.
from tensorflow.keras.layers import Conv2D, MaxPolling2D, Flatten, Dense필요한 클래스를 임포트한다.
합성곱층 쌓기
합성곱층을 추가한다. Conv2D 클래스의 첫 번째 매개변수는 합성곱 커널의 개수이다.
두 번째 매개변수는 합성곱 커널의 크기로 높이와 너비를 튜플로 전달한다.
합성곱 커널로는 전형적으로 3 x 3 또는 5 x 5 크기를 많이 사용한다. activation 매개변수에 렐루 활성화 함수를 지정한다. 패딩은 세임 패딩을 사용하는데, tf.nn.con2d() 함수와는 달리 패딩 매개변수는 대소문자를 구분하지 않는다.
Sequential 클래스에 층을 처음 추가할 때는 배치 차원을 제외한 입력의 크기를 지정한다.
conv1 = tf.keras.Sequential()
conv1.add(Conv2D(10, (3, 3), activation='relu', padding='same', input_shape=(28,28,1)))
풀링층 쌓기
풀링층을 추가한다. MaxPooling2D 클래스의 첫 번째 매개변수는 풀링의 높이와 너비를 나타내는 튜플이며, 스트라이드는 strides 매개변수에 지정할 수 있다. 이 매개변수의 기본값은 풀링의 크기이다.
패딩은 padding 매개변수에 지정하며 기본값은 'valid'이다.
conv1.add(MaxPooling2D((2, 2)))
완전 연결층에 주입할 수 있도록 특성 맵 펼치기
풀링 다음에는 완전 연결층에 연결하기 위해 배치 차원을 제외하고 일렬로 펼쳐야 한다.
conv1.add(Flatten())
완전 연결층 쌓기
마지막으로 완전 연결층을 추가한다. 첫 번째 완전 연결층에는 100개의 뉴런을 사용하고 렐루 활성화 함수를 적용한다.
마지막 출력층에는 10개의 클래스에 대응하는 10개의 뉴런을 사용하고 소프트맥스 활성화 함수를 적용한다.
conv1.add(Dense(100, activation='relu'))
conv1.add(Dense(10, activation='softmax'))모델 구조 살펴보기
케라스를 사용하여 합성곱 신경망을 아주 간단하게 만들었다.
모델의 summary() 메서드를 사용하면 conv1 모델의 구조를 자세히 조사할 수 있다.
conv1.summary()
출력 결과를 보면 합성곱층(Conv2D)의 출력 크기는 배치 차원을 제외하고 28 x 28 x 10이다.
이때 배치 차원이 None인 이유는 배치 입력의 개수는 훈련할 때 전달되는 샘플 개수에 따라 달라지기 때문이다.
합성곱 커널은 10개를 사용했으므로 마지막 차원이 10이다.
모델 파라미터의 개수는 전체 가중치의 크기와 커널마다 하나씩 절편을 추가하면 3 x 3 x 1 x 10 + 10 = 100이다.
풀링층과 특성 맵을 완전 연결층에 펼쳐서 주입하기 위해 추가한 Flatten 층에는 가중치가 없다.
첫 번째 완전 연결층에는 1960개(14 x 14 x 10)의 입력이 100개의 뉴런에 연결된다.
가중치는 뉴런마다 하나씩 있으므로 첫 번째 완전 연결층의 가중치 개수는 196100(1960 x 100 + 100) 개다.
마찬가지로 두 번째 완전 연결층의 가중치 개수는 1010(100 x 10 + 10) 개다.
가중치의 개수를 보면 완전 연결층에 비해 합성곱층의 가중치 개수가 아주 적다.
그래서 합성곱층을 여러 개 추가해도 학습할 모델 파라미터의 개수가 크게 늘지 않아서 계산 효율성이 좋다.
합성곱 신경망 모델 훈련
metrics 매개변수에 'accuracy'를 전달하여 훈련시켜 보자.
conv1.compile(optimizer='adam', loss='categorical_crossentropy',metrics=['accuracy'])최적화 알고리즘으로 기본 경사 하강법만 사용했었다. 이번에는 적응적 학습률 알고리즘 중 하나인 아담(Adam) 옵티마이저를 사용한다. 아담은 Adaptive Moment Estimation을 줄여 만든 이름이다.
아담은 손실 함수의 값이 최적값에 가까워질수록 학습률을 낮춰 손실 함수의 값이 안정적으로 수렴될 수 있게 해 준다.
ConvolutionNetwork 클래스로 수행했던 것과 동일하게 20번의 에포크 동안 훈련해 보자.
history = conv1.fit(x_train, y_train_encoded, epochs=20, validation_data=(x_val, y_val_encoded))plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('iteration')
plt.legend(['train_accuracy', 'val_accuracy'])
plt.show()
검증 세트 정확도가 92%까지 크게 증가했다.
하지만 정확도와 손실을 그래프로 그려보니 몇 번의 에포크 만에 검증 손실이 크게 증가했다.
이는 과대 적합이 일찍 발생했음을 의미한다.
드롭아웃
신경망에서 과대 적합을 줄이는 방법 중 하나는 드롭아웃이다.
드롭아웃은 무작위로 일부 뉴런을 비활성화시킨다. 무작위로 일부 뉴런을 비활성화시키면 특정 뉴런에 과도하게 의존하여 훈련하는 것을 막아준다.
예를 들면 다음과 같다.

만약 2, 3, 30번이 핵심이던 팀에서 2, 3, 30번을 경기에서 제외시킨다면 전력이 크게 감소할 것이다.
따라서 다른 선수들도 고르게 훈련시켜 전력 손실을 최소화해야 한다.
일부 뉴런이 비활성화되었을 때에도 타깃을 잘 예측하려면 특정 뉴런에 과도하게 의존하지 않고 모든 뉴런이 의미 있는 패턴을 학습해야 한다. 뉴런이 훈련 세트에 있는 패턴을 고르게 감지하므로 전체적인 일반화 성능이 높아진다.
드롭아웃은 모델을 학습할 때만 적용한다.
상대적으로 테스트와 실전의 출력값이 훈련할 때의 출력값보다 높아지므로 테스트나 실전에서는 출력값을 드롭아웃 비율만큼 낮춰야 한다.
텐서플로에서는 드롭아웃의 비율만큼 뉴런의 출력을 높인다.
출력값을 드롭아웃 비율만큼 낮춰야 한다. 그런데 텐서플로를 비롯하여 대부분의 딥러닝 프레임워크는 반대로 이 문제를 해결한다.
즉, 훈련할 때 드롭아웃 비율만큼 뉴런의 출력을 높여 훈련시킨다.

드롭아웃의 비율이 0.25(25%)이므로 출력을 33% 정도 증가시킨다. ( 1 / (1 - 0.25) = 1.333...)
실전에서는 드롭아웃되는 뉴런이 없기 때문에 출력을 증가시키지 않는다.
드롭아웃 추가된 모델
conv2 = tf.keras.Sequential()
conv2.add(Conv2D(10, (3, 3), activation='relu', padding='same', input_shape=(28, 28, 1)))
conv2.add(MaxPooling2D((2, 2)))
conv2.add(Flatten())
conv2.add(Dropout(0.5))
conv2.add(Dense(100, activation='relu'))
conv2.add(Dense(10, activation='softmax'))
conv2.summary()
훈련
conv2.compile(optimizer='adam', loss='categorical_crossentropy',metrics=['accuracy'])
history = conv2.fit(x_train, y_train_encoded, epochs=20, validation_data=(x_val, y_val_encoded))plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('iteration')
plt.legend(['train_accuracy', 'val_accuracy'])
plt.show()
