순차 데이터
데이터 중에는 독립적이지 않고 샘플이 서로 연관되어 있는 경우가 있다.
예를 들면 날씨 정보는 샘플이 서로 연관되어 있다. 오후 3시의 온도를 알고 있다면 1시간 후의 온도를 비슷하게 예상할 수 있다. 즉, 온도를 매시간 측정하여 데이터 세트를 만들었다면 각 시간의 온도는 이전 시간의 온도와 깊은 연관이 있을 것이다. 이렇게 일정 시간 간격으로 배치된 데이터를 시계열(time series)데이터라고 부른다.
시계열 데이터를 포함하여 샘플에 순서가 있는 데이터를 일반적으로 순차 데이터(sequential data)라고 부른다.
대표적인 순차 데이터의 예는 텍스트이다. 글을 구성하는 글자와 단어들의 순서가 맞아야 의미가 제대로 전달되기 때문이다. 이때 모델에서 순차 데이터를 처리하는 각 단계를 타입 스텝(time step)이라고 부란다.
3개의 단어로 이루어진 순차 데이터가 있다. 이 데이터의 처리 단위가 단어라면 총 타입 스텝은 3이다.
만약 처리 단위가 글자라면 총 타입 스텝은 19이다.

완전 연결 신경망에 데이터가 주입되 모습을 살펴보자.
완전 연결 신경망이나 합성곱 신경망은 이전의 샘플에 대한 정보를 유지하지 않는다.
또 현재의 샘플을 처리할 때 이전에 어떤 샘플이 주입되었는지도 고려하지 않는다.
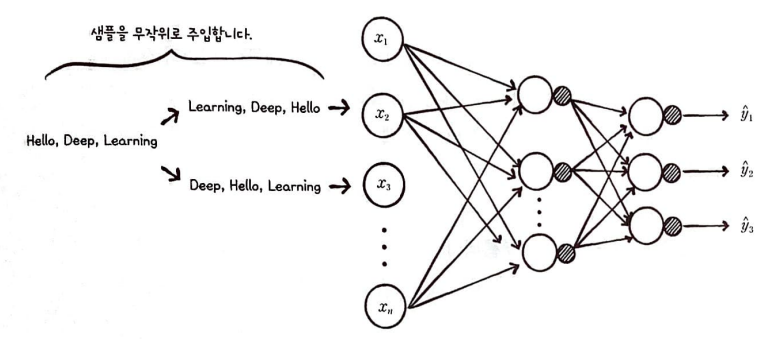
따라서 순서가 있는 데이터를 처리하려면 다른 모델 구조를 고려해야 한다.
순환 신경망
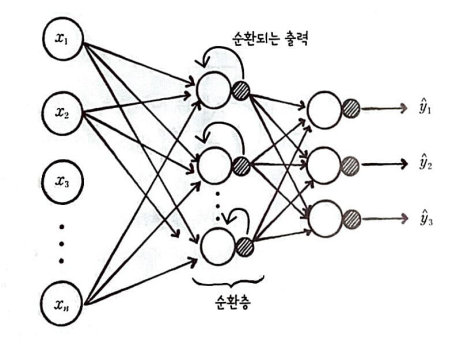
순환 신경망은 뉴런의 출력이 순환되는 신경망을 말한다.
그림을 자세히 보면 지금까지 공부한 인공신경망과 다른 점이 하나 있다.
바로 은닉층의 출력이 다시 은닉층의 입력으로 사용된다는 점이다. 이것을 순환 구조라고 부르며 순환 구조가 있는 층을 순환층이라고 한다.
은닉층에서 순환된 출력은 다음 입력을 처리할 때 현재 입력과 같이 사용된다.
즉, 이전 샘플의 정보를 현재 샘플을 처리할 때 참조할 수 있다.
순환 신경망에서 뉴런은 '셀'
순황 신경망에서는 층이나 뉴런을 셀(cell)이라 부른다. 또한 각 뉴런마다 순환 구조를 표현하기가 번거롭기 때문에 셀 하나에 순환 구조를 나타내는 경우가 많다. 하지만 실제로는 여러 개의 뉴런을 사용하는 것이다.
순환 신경망에서는 셀의 출력을 은닉 상태(hidden state)라고 부른다.
입력은 x, 출력은 h라고 표시한다.
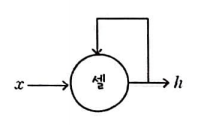
현재의 은닉 상태 h를 계산하기 위해 이전 타임 스텝의 은닉 상태를 사용한다.
순환층의 셀에서 입력과 이전 타임 스텝의 은닉 상태를 통해 어떤 계산을 해야 하는지 살펴보자.
순환층의 셀에서 수행되는 계산은 정방향 계산과 비슷하지만 이전 타임 스텝의 은닉 상태와 곱하는 가중치가 하나 더 있다.
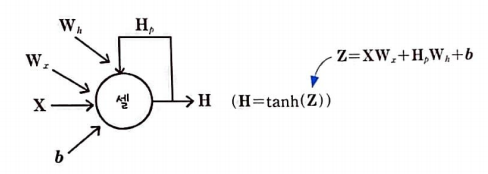
입력 X와 이전 타임 스텝의 은닉 상태 H_p에 곱해지는 2개의 가중치 W_x와 W_h 그리고 절편 b를 함께 표시했다.
또 순환 신경망의 셀에서는 활성화 함수로 하이퍼볼록 탄젠트(hyperbolic tangent) 함수를 많이 사용한다.
따라서, 은닉 상태 H를 tanh로 표현한다.
순환 신경망 정방향 계산
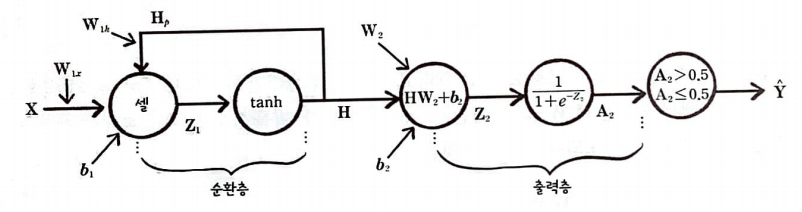
순환층의 가중치에는 첫 번째 층이라는 의미로 아래 첨자 1을 붙여 표기했다.
위 신경망은 이진 분류 문제를 가정했으므로 출력층의 활성화 함수로 시그모이드 함수를 사용했다.

각 층의 정방향 계산식은 위와 같다. 입력과 가중치의 구조를 알아보자.
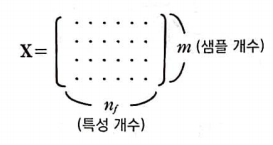
입력 데이터 X의 크기는 (m, n_f)이다. m은 샘플의 개수이고, n_f는 특성 개수이다.
가중치 W_1x의 크기는 (n_f, n_c)이다. n_c는 순환층에 있는 셀의 개수이다.
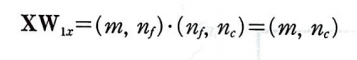
XW_1x의 크기가 (m, n_c)이므로 Z_1과 H 그리고 이전 은닉 상태인 H_p 크기도 (m, n_c)가 될 것이다.
두 행렬을 곱한 H_pW_1h의 크기는 (m, n_c)가 된다. 따라서, W_1h의 크기가 (n_c, n_c)가 되어야 한다.
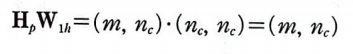
출력층의 계산은 쉽다.
출력층으로 전달되는 H의 크기가 (m, n_c)이므로 이와 곱해지는 가중치 W_2의 크기는 (n_c, n_classes)이다.
따라서 Z_2, A_2의 크기는 (m, n_classes)이다.
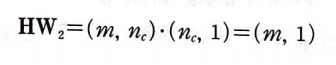
순환층과 출력층의 절편 크기는 쉽게 추측할 수 있다.
각 층의 뉴런마다 절편이 하나씩 필요하므로 b_1의 크기는 (n_c, 1)이고 b_2의 크기는 (n_classes, )이다.
순환 신경망 역방향 계산
미분의 연쇄 법칙을 적용하여 역방향 계산을 진행한다.
가중치 W_2에 대한 손실 함수 도함수
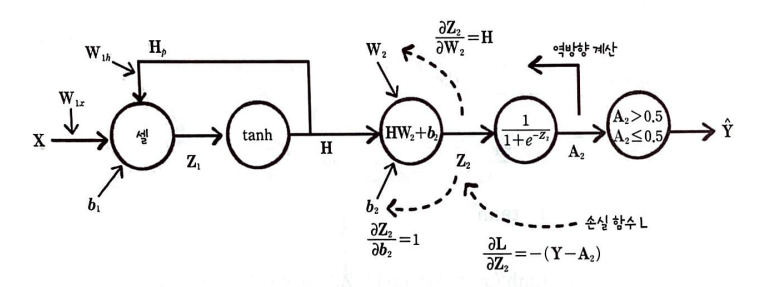
출력층의 가중치 W_2에 대한 손실함수 L을 미분하기 위해 연쇄 법칙을 적용하면 다음과 같다.
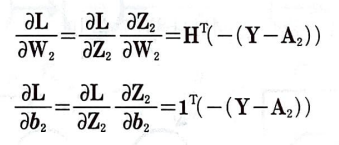
완전 연결 신경망에 있는 은닉층의 출력 A_1을 셀의 출력 H로 바꾼 것 외에는 동일하다.
이어서 H에 대한 Z_2의 도함수를 알아보자.
H에 대한 Z_2의 도함수
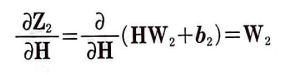
Z_1에 대한 H의 도함수
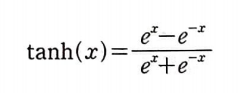
하이퍼볼릭 탄젠트 함수의 도함수이다. 이를 x에 대하여 미분을 진행하면 다음과 같다.
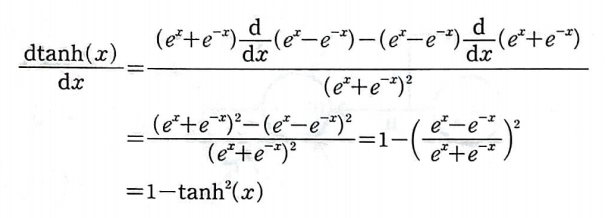
Z_1에 대한 H의 도함수를 적용해 보자.
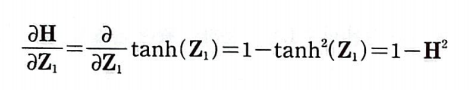
지금까지의 도함수를 그림으로 정리하면 다음과 같다.
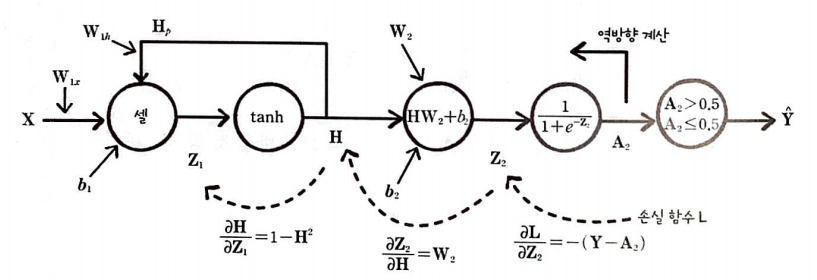
연쇄 법칙을 적용하여 식으로 나타내보자.
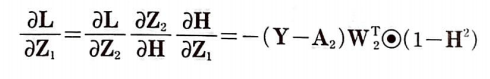
가중치 W_1h에 대한 Z_1의 도함수
가중치 W_1h의 업데이트에 사용할 W_1h에 대한 Z_1의 도함수(그레이디언트)를 구할 차례이다.
W_1h에 대한 Z_1의 도함수는 다음과 같다. 하지만 유의해야 할 점이 있다.
H_p도 W_1h를 사용하기 때문에 편미분 할 때 상수로 취급할 수 없다.
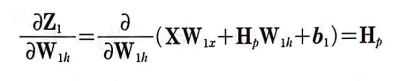
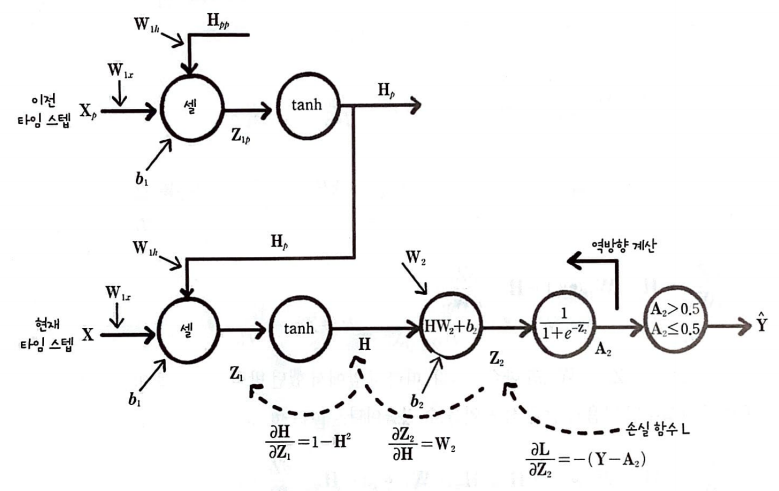
이런 그림을 보고 신경망을 타임 스텝으로 펼쳤다고 한다.
그림을 보면 이전 타임 스텝의 은닉 상태 H_p도 W_1h에 의해 영향을 받고 있다.
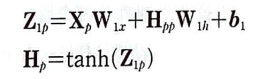
H_p는 이전 타임 스텝의 입력 X_p와 두 타임 스텝 이전의 은닉 상태 H_pp를 사용해 계산한다.
여기서 중요한 점은 타임 스텝마다 같은 가중치를 사용한다는 점이다.
즉, 타임 스텝의 은닉 상태를 계산하기 위해 사용하는 W_1x, W_1h, b1은 동일하다.
가중치는 훈련 데이터에 있는 시퀀스를 차례대로 모두 진행한 후 마지막에 업데이트된다.
따라서, 상수 취급을 하지 않고 미분을 진행해야 한다.
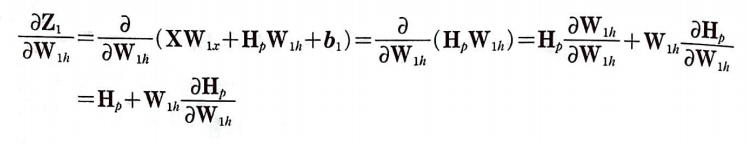
첫 번째 항은 H_p를 상수처럼 취급하고 두 번째 항은 W_1h를 상수처럼 취급한다.
이제 남은 부분도 연쇄 법칙을 적용하자.
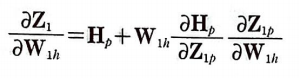
활성화 함수 tanh의 미분을 앞에서 유도해 보았기 때문에 다음과 같이 나타낼 수 있다.
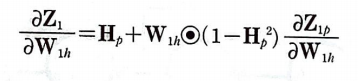
남은 부분인 Z_1p는 W_1h의 함수이다. 따라서 앞에서 했던 방식을 그대로 이전 타임 스텝에 대해 반복하면 다음과 같은 식을 얻을 수 있다.
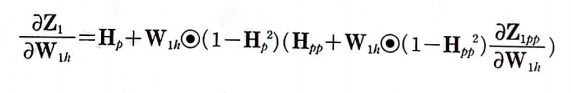
계속하여 이전 타임 스텝에 대한 식이 나온다.
이런 식으로 순환 신경망에 주입한 모든 타임 스텝을 거슬러 올라갈 때까지 계속된다.
이를 시간을 거슬러 역전파(Backporpagation Through Time: BPTT)된다고 한다.
순환 구조 때문에 셀의 가중치에 대한 손실 함수를 구하려면 어쩔 수 없이 타임 스텝을 거슬러 역전파할 수밖에 없다.
각 타임 스텝마다 셀의 출력을 모두 기록해서 가지고 있어야 한다. (H_p, H_pp, H_ppp....)
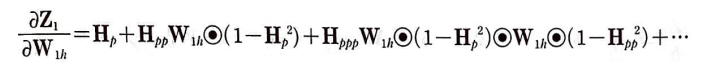
가중치 W_1x에 대한 Z_1의 도함수
가중치 W_1x에 대한 그레이디언트를 업데이트하기 위해 도함수를 구하면 다음과 같다.
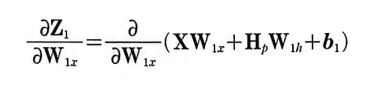
첫 번째 항의 도함수는 X이고 b_1은 W_1x의 함수가 아니라 상수 취급한다.
문제는 두 번째 항이다. H_p가 W_1x의 함수이기 때문이다. W_1h때와 마찬가지로 전개해보자.
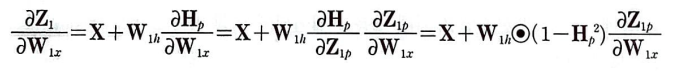
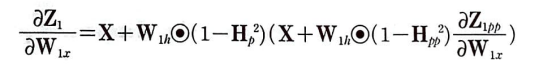
W_1h와 같이 계속하여 연계된다.
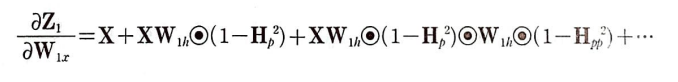
절편 b_1에 대한 Z_1의 도함수
b_1에 대한 Z_1의 도함수를 구해보자. 여기서도 마찬가지로 H_p가 b_1의 함수이다.

손실 함수에 대한 그레이디언트, 순환 셀의 그레이디언트 모두 구해보았다.
앞으로 손실 함수에 대한 그레이디언트를 err_to_cell이라고 표현하고, W_1x, W_1h, b_1에 업데이트할 최종 그레이디언트는 err_to_cell과 각각의 도함수를 곱해서 구한다.
순차 데이터
데이터 중에는 독립적이지 않고 샘플이 서로 연관되어 있는 경우가 있다.
예를 들면 날씨 정보는 샘플이 서로 연관되어 있다. 오후 3시의 온도를 알고 있다면 1시간 후의 온도를 비슷하게 예상할 수 있다. 즉, 온도를 매시간 측정하여 데이터 세트를 만들었다면 각 시간의 온도는 이전 시간의 온도와 깊은 연관이 있을 것이다. 이렇게 일정 시간 간격으로 배치된 데이터를 시계열(time series)데이터라고 부른다.
시계열 데이터를 포함하여 샘플에 순서가 있는 데이터를 일반적으로 순차 데이터(sequential data)라고 부른다.
대표적인 순차 데이터의 예는 텍스트이다. 글을 구성하는 글자와 단어들의 순서가 맞아야 의미가 제대로 전달되기 때문이다. 이때 모델에서 순차 데이터를 처리하는 각 단계를 타입 스텝(time step)이라고 부란다.
3개의 단어로 이루어진 순차 데이터가 있다. 이 데이터의 처리 단위가 단어라면 총 타입 스텝은 3이다.
만약 처리 단위가 글자라면 총 타입 스텝은 19이다.

완전 연결 신경망에 데이터가 주입되 모습을 살펴보자.
완전 연결 신경망이나 합성곱 신경망은 이전의 샘플에 대한 정보를 유지하지 않는다.
또 현재의 샘플을 처리할 때 이전에 어떤 샘플이 주입되었는지도 고려하지 않는다.

따라서 순서가 있는 데이터를 처리하려면 다른 모델 구조를 고려해야 한다.
순환 신경망

순환 신경망은 뉴런의 출력이 순환되는 신경망을 말한다.
그림을 자세히 보면 지금까지 공부한 인공신경망과 다른 점이 하나 있다.
바로 은닉층의 출력이 다시 은닉층의 입력으로 사용된다는 점이다. 이것을 순환 구조라고 부르며 순환 구조가 있는 층을 순환층이라고 한다.
은닉층에서 순환된 출력은 다음 입력을 처리할 때 현재 입력과 같이 사용된다.
즉, 이전 샘플의 정보를 현재 샘플을 처리할 때 참조할 수 있다.
순환 신경망에서 뉴런은 '셀'
순황 신경망에서는 층이나 뉴런을 셀(cell)이라 부른다. 또한 각 뉴런마다 순환 구조를 표현하기가 번거롭기 때문에 셀 하나에 순환 구조를 나타내는 경우가 많다. 하지만 실제로는 여러 개의 뉴런을 사용하는 것이다.
순환 신경망에서는 셀의 출력을 은닉 상태(hidden state)라고 부른다.
입력은 x, 출력은 h라고 표시한다.

현재의 은닉 상태 h를 계산하기 위해 이전 타임 스텝의 은닉 상태를 사용한다.
순환층의 셀에서 입력과 이전 타임 스텝의 은닉 상태를 통해 어떤 계산을 해야 하는지 살펴보자.
순환층의 셀에서 수행되는 계산은 정방향 계산과 비슷하지만 이전 타임 스텝의 은닉 상태와 곱하는 가중치가 하나 더 있다.

입력 X와 이전 타임 스텝의 은닉 상태 H_p에 곱해지는 2개의 가중치 W_x와 W_h 그리고 절편 b를 함께 표시했다.
또 순환 신경망의 셀에서는 활성화 함수로 하이퍼볼록 탄젠트(hyperbolic tangent) 함수를 많이 사용한다.
따라서, 은닉 상태 H를 tanh로 표현한다.
순환 신경망 정방향 계산

순환층의 가중치에는 첫 번째 층이라는 의미로 아래 첨자 1을 붙여 표기했다.
위 신경망은 이진 분류 문제를 가정했으므로 출력층의 활성화 함수로 시그모이드 함수를 사용했다.

각 층의 정방향 계산식은 위와 같다. 입력과 가중치의 구조를 알아보자.
입력 데이터 X의 크기는 (m, n_f)이다. m은 샘플의 개수이고, n_f는 특성 개수이다.

가중치 W_1x의 크기는 (n_f, n_c)이다. n_c는 순환층에 있는 셀의 개수이다.
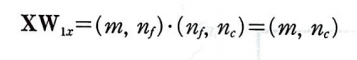
XW_1x의 크기가 (m, n_c)이므로 Z_1과 H 그리고 이전 은닉 상태인 H_p 크기도 (m, n_c)가 될 것이다.
두 행렬을 곱한 H_pW_1h의 크기는 (m, n_c)가 된다. 따라서, W_1h의 크기가 (n_c, n_c)가 되어야 한다.
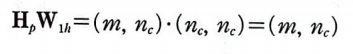
출력층의 계산은 쉽다.
출력층으로 전달되는 H의 크기가 (m, n_c)이므로 이와 곱해지는 가중치 W_2의 크기는 (n_c, n_classes)이다.
따라서 Z_2, A_2의 크기는 (m, n_classes)이다.
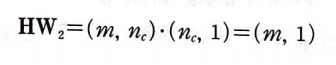
순환층과 출력층의 절편 크기는 쉽게 추측할 수 있다.
각 층의 뉴런마다 절편이 하나씩 필요하므로 b_1의 크기는 (n_c, 1)이고 b_2의 크기는 (n_classes, )이다.
순환 신경망 역방향 계산
미분의 연쇄 법칙을 적용하여 역방향 계산을 진행한다.
가중치 W_2에 대한 손실 함수 도함수

출력층의 가중치 W_2에 대한 손실함수 L을 미분하기 위해 연쇄 법칙을 적용하면 다음과 같다.
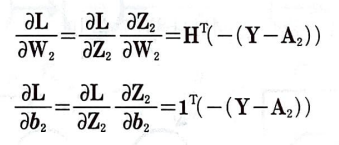
완전 연결 신경망에 있는 은닉층의 출력 A_1을 셀의 출력 H로 바꾼 것 외에는 동일하다.
이어서 H에 대한 Z_2의 도함수를 알아보자.
H에 대한 Z_2의 도함수
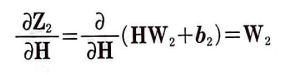
Z_1에 대한 H의 도함수
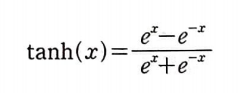
하이퍼볼릭 탄젠트 함수의 도함수이다. 이를 x에 대하여 미분을 진행하면 다음과 같다.
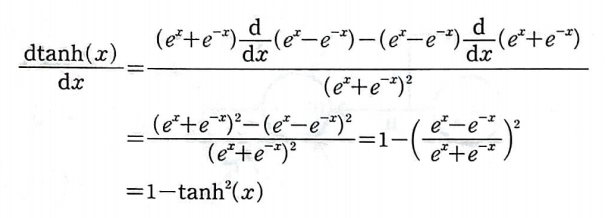
Z_1에 대한 H의 도함수를 적용해 보자.
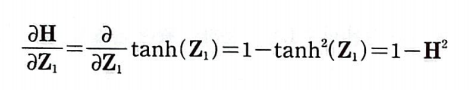
지금까지의 도함수를 그림으로 정리하면 다음과 같다.

연쇄 법칙을 적용하여 식으로 나타내보자.
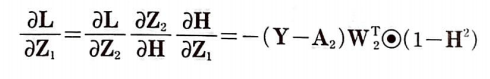
가중치 W_1h에 대한 Z_1의 도함수
가중치 W_1h의 업데이트에 사용할 W_1h에 대한 Z_1의 도함수(그레이디언트)를 구할 차례이다.
W_1h에 대한 Z_1의 도함수는 다음과 같다. 하지만 유의해야 할 점이 있다.
H_p도 W_1h를 사용하기 때문에 편미분 할 때 상수로 취급할 수 없다.
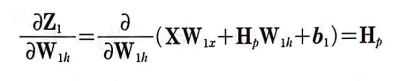

이런 그림을 보고 신경망을 타임 스텝으로 펼쳤다고 한다.
그림을 보면 이전 타임 스텝의 은닉 상태 H_p도 W_1h에 의해 영향을 받고 있다.
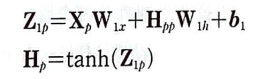
H_p는 이전 타임 스텝의 입력 X_p와 두 타임 스텝 이전의 은닉 상태 H_pp를 사용해 계산한다.
여기서 중요한 점은 타임 스텝마다 같은 가중치를 사용한다는 점이다.
즉, 타임 스텝의 은닉 상태를 계산하기 위해 사용하는 W_1x, W_1h, b1은 동일하다.
가중치는 훈련 데이터에 있는 시퀀스를 차례대로 모두 진행한 후 마지막에 업데이트된다.
따라서, 상수 취급을 하지 않고 미분을 진행해야 한다.
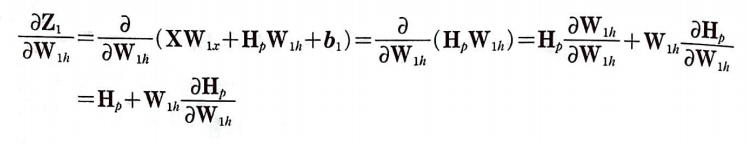
첫 번째 항은 H_p를 상수처럼 취급하고 두 번째 항은 W_1h를 상수처럼 취급한다.
이제 남은 부분도 연쇄 법칙을 적용하자.
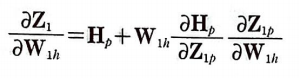
활성화 함수 tanh의 미분을 앞에서 유도해 보았기 때문에 다음과 같이 나타낼 수 있다.
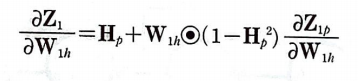
남은 부분인 Z_1p는 W_1h의 함수이다. 따라서 앞에서 했던 방식을 그대로 이전 타임 스텝에 대해 반복하면 다음과 같은 식을 얻을 수 있다.
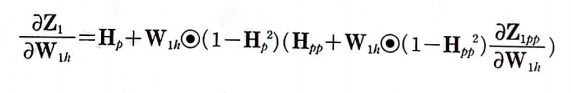
계속하여 이전 타임 스텝에 대한 식이 나온다.
이런 식으로 순환 신경망에 주입한 모든 타임 스텝을 거슬러 올라갈 때까지 계속된다.
이를 시간을 거슬러 역전파(Backporpagation Through Time: BPTT)된다고 한다.
순환 구조 때문에 셀의 가중치에 대한 손실 함수를 구하려면 어쩔 수 없이 타임 스텝을 거슬러 역전파할 수밖에 없다.
각 타임 스텝마다 셀의 출력을 모두 기록해서 가지고 있어야 한다. (H_p, H_pp, H_ppp....)
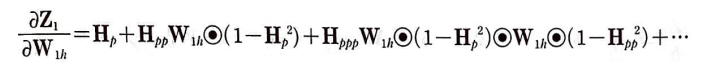
가중치 W_1x에 대한 Z_1의 도함수
가중치 W_1x에 대한 그레이디언트를 업데이트하기 위해 도함수를 구하면 다음과 같다.
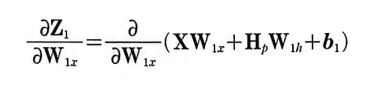
첫 번째 항의 도함수는 X이고 b_1은 W_1x의 함수가 아니라 상수 취급한다.
문제는 두 번째 항이다. H_p가 W_1x의 함수이기 때문이다. W_1h때와 마찬가지로 전개해보자.
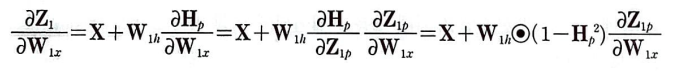
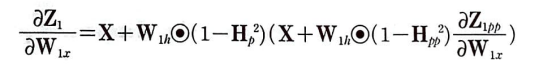
W_1h와 같이 계속하여 연계된다.
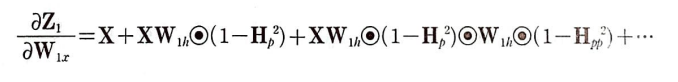
절편 b_1에 대한 Z_1의 도함수
b_1에 대한 Z_1의 도함수를 구해보자. 여기서도 마찬가지로 H_p가 b_1의 함수이다.

손실 함수에 대한 그레이디언트, 순환 셀의 그레이디언트 모두 구해보았다.
앞으로 손실 함수에 대한 그레이디언트를 err_to_cell이라고 표현하고, W_1x, W_1h, b_1에 업데이트할 최종 그레이디언트는 err_to_cell과 각각의 도함수를 곱해서 구한다.
