그래프(Graph)란?
그래프는 노드(node, 혹은 정점(vertex))와 그들을 잇는 간선(edge)으로 구성되어 있다.
경로(path)는 한 노드에서 그래프의 간선을 지나 다른 노드까지 가는 길을 의미한다. 경로의 길이는 경로에 포함된 간서의 개수이다.
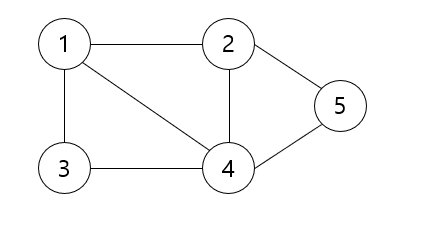
예를 들어 1번 노드에서 5번 노드로 가는 길이가 3인 경로( 1 -> 3 -> 4 -> 5)가 나와 있다.
사이클(Cycle)은 처음 노드와 마지막 노드가 같은 경로를 의미한다. 예를 들어 1 -> 3 -> 4 -> 1로 구성된 사이클이 존재한다.
그래프의 모든 노드 간에 경로가 있는 경우를 연결 그래프(connected graph)라고 한다.
 연결 그래프 |
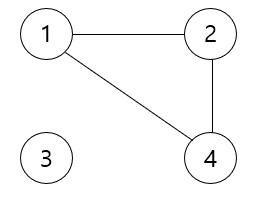 연결 그래프가 아님 |
그래프의 연결된 부분을 컴포넌트(component)라고 표현한다. 연결 그래프가 아닌 그래프를 보면 {1, 2, 4} , {3}의 컴포넌트가 존재한다.
트리(Tree)는 사이클이 없는 연결 그래프를 말한다. 방향 그래프(Directed graph)에서는 간선의 한 방향으로만 이동할 수 있다. 가중 그래프(weighted graph)는 간선마다 가중치(weight)가 존재하는 그래프이다.
두 노드를 잇는 간선이 있을 때 두 노드를 이웃(neighbor) 노드, 또는 인접한(adjacent) 노드라고 표현한다.
노드의 차수(dgree)는 이웃 노드의 개수이다.

1번 노드의 차수는 3이고, 5번 노드의 차수는 5이다.
그래프의 간선 개수를 m이라고 할 때, 차수의 합은 항상 2m이다. 각 간선은 그 간선이 잇는 두 노드의 차수를 1씩 증가시키기 때문이다. 모든 노드의 차수가 d로 같은 경우를 정규 그래프(regular graph)라고 하며, 모든 노드의 차수가 n-1(노드의 개수보다 1작은 수)인 경우, 즉 모든 두 노드 간에 간선이 있는 경우를 완전 그래프(complete graph)라고 한다.
방향 그래프에서 특정 노드로 접근하여 들어오는 간선의 개수를 진입 차수(indegree), 밖으로 나가는 간선의 개수를
진출 차수(outdegree)라고 한다.
어떤 그래프의 모든 노드를 두 가지 색깔 중 하나로 칠하되, 이웃 노드의 색깔이 같은 경우가 없도록 만들 수 있다면 그 그래프를 이분 그래프(biparite graph)라고 한다. 이분 그래프는 홀수 개의 간선으로 이루어진 사이클이 없는 경우와 일치한다.
그래프(Graph)란?
그래프는 노드(node, 혹은 정점(vertex))와 그들을 잇는 간선(edge)으로 구성되어 있다.
경로(path)는 한 노드에서 그래프의 간선을 지나 다른 노드까지 가는 길을 의미한다. 경로의 길이는 경로에 포함된 간서의 개수이다.

예를 들어 1번 노드에서 5번 노드로 가는 길이가 3인 경로( 1 -> 3 -> 4 -> 5)가 나와 있다.
사이클(Cycle)은 처음 노드와 마지막 노드가 같은 경로를 의미한다. 예를 들어 1 -> 3 -> 4 -> 1로 구성된 사이클이 존재한다.
그래프의 모든 노드 간에 경로가 있는 경우를 연결 그래프(connected graph)라고 한다.
 연결 그래프 |
 연결 그래프가 아님 |
그래프의 연결된 부분을 컴포넌트(component)라고 표현한다. 연결 그래프가 아닌 그래프를 보면 {1, 2, 4} , {3}의 컴포넌트가 존재한다.
트리(Tree)는 사이클이 없는 연결 그래프를 말한다. 방향 그래프(Directed graph)에서는 간선의 한 방향으로만 이동할 수 있다. 가중 그래프(weighted graph)는 간선마다 가중치(weight)가 존재하는 그래프이다.
두 노드를 잇는 간선이 있을 때 두 노드를 이웃(neighbor) 노드, 또는 인접한(adjacent) 노드라고 표현한다.
노드의 차수(dgree)는 이웃 노드의 개수이다.

1번 노드의 차수는 3이고, 5번 노드의 차수는 5이다.
그래프의 간선 개수를 m이라고 할 때, 차수의 합은 항상 2m이다. 각 간선은 그 간선이 잇는 두 노드의 차수를 1씩 증가시키기 때문이다. 모든 노드의 차수가 d로 같은 경우를 정규 그래프(regular graph)라고 하며, 모든 노드의 차수가 n-1(노드의 개수보다 1작은 수)인 경우, 즉 모든 두 노드 간에 간선이 있는 경우를 완전 그래프(complete graph)라고 한다.
방향 그래프에서 특정 노드로 접근하여 들어오는 간선의 개수를 진입 차수(indegree), 밖으로 나가는 간선의 개수를
진출 차수(outdegree)라고 한다.
어떤 그래프의 모든 노드를 두 가지 색깔 중 하나로 칠하되, 이웃 노드의 색깔이 같은 경우가 없도록 만들 수 있다면 그 그래프를 이분 그래프(biparite graph)라고 한다. 이분 그래프는 홀수 개의 간선으로 이루어진 사이클이 없는 경우와 일치한다.
