동적 계획법 예제(2). 백준 [9095] 1, 2, 3 더하기

백준 [9095]

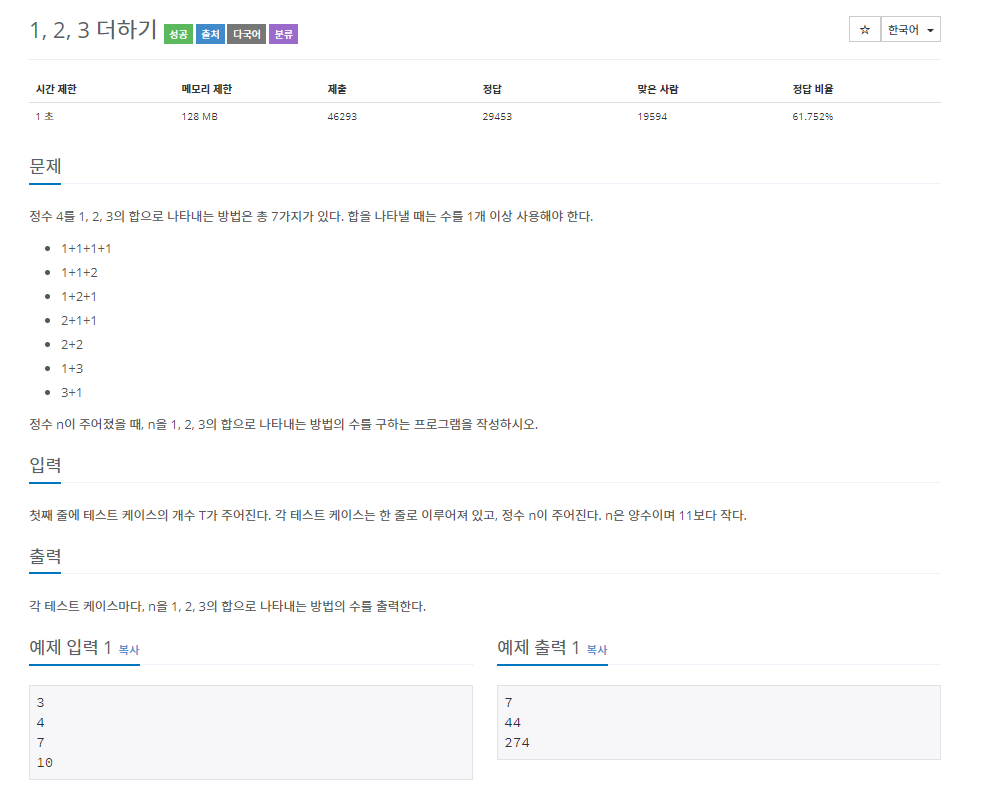
동적 계획법의 예제이다. 우선, 몇 개의 정수를 처리할지 입력받은 후 입력받은 개수만큼의 입력을 받는다.
그 후, 입력받은 수들을 1, 2, 3의 합으로만 나타내는 방법의 총 개수를 구하는 문제이다.

예를 들어 4는 1+1+1+1, 1+1+2, 1+2+1, 1+3, 2+1+1, 2+2, 3+1로 총 7개이다. 규칙은 간단하다. 
1과 2 그리고 3을 선택한다는 가정을하면 만들려는 수에서 선택한 수를 뺀 수를 만드는 경우의 수를 모두 더하면 되는 것이다.

1을 먼저 선택한 경우 1 + 3을 만드는 경우( 1+1+1, 1+2, 2+1, 3) => 4가지
2를 먼저 선택한 경우 2 + 2를 만드는 경우( 1+1, 2) => 2가지
3을 먼저 선택한 경우 3+ 1을 만드는 경우( 1 ) => 1가지
모두 더하면 7개의 경우의 수가 생긴다.

그렇다면 점화식은 다음과 같다.
f(n) = f(n-1) + f(n-2) + f(n-3) 
(단, 0, 1, 2는 기저 조건으로 각각 1개, 1개, 2개의 경우의 수를 갖는다. n-3이 음수가 되면 안 되고, 0을 만드는 경우는 0을 선택했을 경우 1가지이다. 하지만, 0은 입력으로는 받지 않는다.)

다음은 java로 작성한 코드이다.

import java.util.Scanner;

public class Main {

		public static void main(String[] args) {
        
		//스캐너
		Scanner scan = new Scanner(System.in);

		int x = scan.nextInt();

		//목표 수의 배열
		int target[] = new int [x];

		for(int i = 0 ; i < x ; i++) {
			target[i] = scan.nextInt();
		}
		
		//경우의 수 배열
		int solution[];


		for(int a=0; a<x ; a++) {
			
			//1이나 2가 입력으로 들어오면 각각의 경우의 수를 return
			if(target[a]==1) {
				System.out.println(1);
				continue;
			}else if(target[a]==2) {
				System.out.println(2);
				continue;
			}
			
			solution = new int [target[a]+1];

			//기저조건
			solution[0] = 1;
			solution[1] = 1;
			solution[2] = 2;
			
			for(int i = 3 ; i <= target[a] ; i ++) {
				solution[i] = solution[i-3] + solution[i-2] + solution[i-1];
			}
			System.out.println(solution[target[a]]);
		}



	}

}

target []은 만들고자 하는 수들의 배열이고, solution은 목표로 하는 수까지의 경우의 수들의 배열이다.
기저 조건을 설정하고 점화식에 맞춰 작성한다.