문제 설명
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
풀이
우선 문제를 분석해 보면 여러 경기를 통해 순위가 정해지는 선수의 수를 세는 문제이다.
그렇다면 순위가 정해지는 선수는 모든 선수와의 관계가 정해져야 된다는 뜻이다.
이때 관계는 직접적, 간접적 모두 가능하다.
그래프를 그려 문제를 이해하면 쉽다.
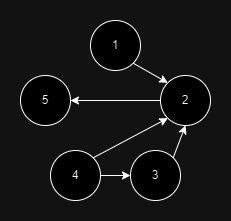
예제의 경우 2는 다른 모든 선수와 관계가 정의되어 있다.
1, 3, 4에게는 지고 5에게는 이긴다.
또한, 5도 다른 모든 선수와 관계가 있다.
1, 3, 4는 2를 이기는데 2가 5를 이기므로 5는 1, 2, 3, 4에게 진다.
즉, 방향 그래프를 통해 간선을 만들고 모든 노드에서 순회를 한 뒤 방문 여부를 기록한다.
그 뒤, 한 노드에서 다른 노드를 모두 방문할 수 있다면 그 노드는 순위가 정해지는 것이다.
이때, 관계가 있다는 뜻은 A → B도 가능하고 B → A도 가능하다.
즉, 5에서 1을 방문할 수 없지만, 1에서 5는 방문할 수 있다.
이러한 경우 1과 5는 간접적으로 관계가 있는 것이다.
전체 코드
#include <string>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
void BFS(vector<vector<int>>& edge, vector<vector<bool>>& rel, int start, int n)
{
queue<int> q;
q.push(start);
vector<bool> visited(n+1, false);
while(!q.empty())
{
int cur = q.front();
q.pop();
for(auto next : edge[cur])
{
if(visited[next]) continue;
visited[next] = true;
rel[start][next] = true;
q.push(next);
}
}
}
int solution(int n, vector<vector<int>> results) {
int answer = 0;
vector<int> rank(n+1, 0);
vector<vector<bool>> rel(n+1, vector(n+1, false));
vector<vector<int>> edge(n+1);
for(auto result : results)
{
rel[result[0]][result[1]] = true;
edge[result[0]].push_back(result[1]);
}
for(int i = 1; i <= n; i++)
{
BFS(edge, rel, i, n);
}
for(int i = 1; i <= n; i++)
{
rel[i][i] = true;
}
for(int i = 1; i <= n; i++)
{
bool flag = true;
for(int j = 1; j <= n; j++)
{
if(!rel[i][j])
{
if(!rel[j][i])
{
flag = false;
break;
}
}
}
if(flag)
{
answer++;
}
}
return answer;
}
문제 설명
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
풀이
우선 문제를 분석해 보면 여러 경기를 통해 순위가 정해지는 선수의 수를 세는 문제이다.
그렇다면 순위가 정해지는 선수는 모든 선수와의 관계가 정해져야 된다는 뜻이다.
이때 관계는 직접적, 간접적 모두 가능하다.
그래프를 그려 문제를 이해하면 쉽다.

예제의 경우 2는 다른 모든 선수와 관계가 정의되어 있다.
1, 3, 4에게는 지고 5에게는 이긴다.
또한, 5도 다른 모든 선수와 관계가 있다.
1, 3, 4는 2를 이기는데 2가 5를 이기므로 5는 1, 2, 3, 4에게 진다.
즉, 방향 그래프를 통해 간선을 만들고 모든 노드에서 순회를 한 뒤 방문 여부를 기록한다.
그 뒤, 한 노드에서 다른 노드를 모두 방문할 수 있다면 그 노드는 순위가 정해지는 것이다.
이때, 관계가 있다는 뜻은 A → B도 가능하고 B → A도 가능하다.
즉, 5에서 1을 방문할 수 없지만, 1에서 5는 방문할 수 있다.
이러한 경우 1과 5는 간접적으로 관계가 있는 것이다.
전체 코드
#include <string>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
void BFS(vector<vector<int>>& edge, vector<vector<bool>>& rel, int start, int n)
{
queue<int> q;
q.push(start);
vector<bool> visited(n+1, false);
while(!q.empty())
{
int cur = q.front();
q.pop();
for(auto next : edge[cur])
{
if(visited[next]) continue;
visited[next] = true;
rel[start][next] = true;
q.push(next);
}
}
}
int solution(int n, vector<vector<int>> results) {
int answer = 0;
vector<int> rank(n+1, 0);
vector<vector<bool>> rel(n+1, vector(n+1, false));
vector<vector<int>> edge(n+1);
for(auto result : results)
{
rel[result[0]][result[1]] = true;
edge[result[0]].push_back(result[1]);
}
for(int i = 1; i <= n; i++)
{
BFS(edge, rel, i, n);
}
for(int i = 1; i <= n; i++)
{
rel[i][i] = true;
}
for(int i = 1; i <= n; i++)
{
bool flag = true;
for(int j = 1; j <= n; j++)
{
if(!rel[i][j])
{
if(!rel[j][i])
{
flag = false;
break;
}
}
}
if(flag)
{
answer++;
}
}
return answer;
}