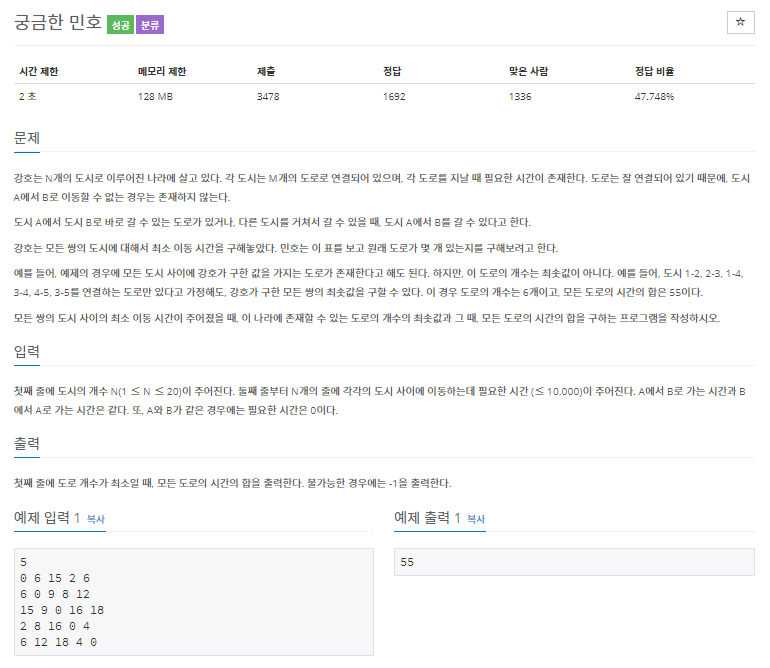
플루이드-워셜 알고리즘의 원리를 이용하여 정답을 구해내는 문제이다.
입력값으로 N개의 도시와 미리 계산해놓은 최솟값들을 입력받기 때문에 플루이드-워셜 알고리즘을 역으로 돌리며 인접 행렬을 구해내면 문제를 풀어낼 수 있다.
다음은 Java로 작성한 코드이다.
import java.util.Scanner;
public class RoadSum {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[][] map = new int[n][n];
int[][] adj = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
map[i][j] = scan.nextInt();
adj[i][j] = map[i][j];
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(i != k && i != j && j != k) {
if(map[i][j] == map[i][k]+map[k][j]) {
adj[i][j] = 0;
}else if(map[i][j] > map[i][k] + map[k][j]){
System.out.println(-1);
return;
}
}
}
}
}
int sum = 0 ;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum += adj[i][j];
}
}
System.out.println(sum/2);
}
}
map[][]은 입력을 받아 저장할 배열이다. 즉, 이미 만들어진 최단거리 배열을 뜻한다.
adj [][]는 인접 행렬이다. 답으로 구할 요소들을 저장할 배열이다.
시작 노드와 중간 노드가 같지 않고, 중간 노드와 도착 노드가 같지 않으며, 시작 노드와 도착 노드 또한 같지 않아야 한다. 그중, 시작~도착 == 시작~중간 + 중간~도착 인경우는 플루이드-워셜 알고리즘이 적용된 부분이라 판단하여, 해당 부분을 0으로 바꾼다. ( 알고리즘이 적용된 부분은 직접 연결되어 있지 않는 부분이다 )
또한, 시작~도착 > 시작~중간 + 중간~도착인 경우는 존재할 수 없다. 따라서 구할 수 없는 잘못된 데이터이기 때문에 조건에 맞게 -1을 출력하고 종료시킨다.
