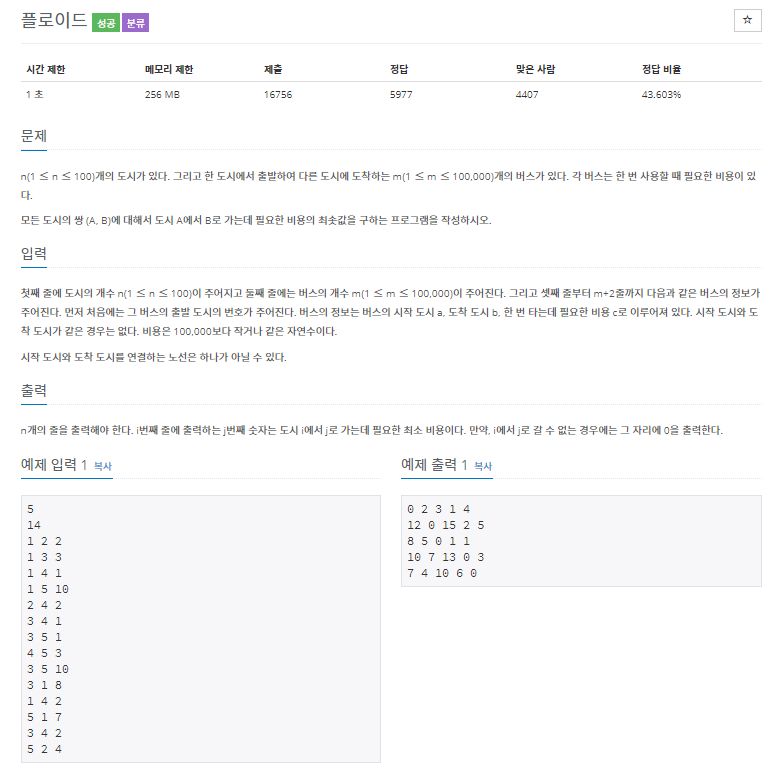
플로이드 알고리즘을 이용하여 최단거리를 구해내는 문제이다.
입력받는 값들은 도시의 개수, 버스의 개수, 버스의 시작, 도착, 가중치이다.
최단 거리를 구하기 위해서는 입력받을 때부터 시작 노드와 도착 노드가 동일한 노드 중 가중치가 작은 노드를 택해서 입력받아 저장해야 한다.
따라서 입력받을때 비교하여 인접 행렬을 만들어야 한다.
인접 행렬을 만든 다음에는 직접 연결되어 방문이 가능한 노드는 플로이드 알고리즘을 이용하여 최솟값을 찾아 나가고 직접 연결이 되어 있지 않은 노드는 다른 노드를 거쳐 이동하게 하여야 한다.
하지만, 이 때, 인접 행렬에서 0인 노드로는 접근이 아예 불가능하기 때문에, 이를 고려하여 알고리즘을 작성해야 한다.
다음은 Java로 작성한 코드이다.
import java.util.Scanner;
public class Bus {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int city = scan.nextInt();
int bus = scan.nextInt();
int[][] map = new int[city+1][city+1];
for (int i = 1; i <= city; i++) {
for (int j = 1; j <= city; j++) {
map[i][j] = 0;
}
}
int row;
int column;
int temp;
for (int k = 0; k < bus; k++) {
row = scan.nextInt();
column = scan.nextInt();
temp = scan.nextInt();
if(map[row][column] != 0 ) {
map[row][column] = Math.min(map[row][column], temp);
continue;
}
map[row][column] = temp;
}
for (int k = 1; k <= city; k++) {
for (int i = 1; i <= city; i++) {
if(map[i][k] == 0)
continue;
for (int j = 1; j <= city; j++) {
if(map[k][j] == 0 || i==j) {
continue;
}else if(map[i][j] == 0 || map[i][j] > map[i][k] + map[k][j]){
map[i][j] = map[i][k] + map[k][j];
}
}
}
}
for (int i = 1; i <= city; i++) {
for (int j = 1; j <= city; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
}
기본원리는 다음과 같다.
앞서 말했듯이 시작 노드와 도착 노드가 같다면 가중치가 적은 간선을 택하여 저장한다.
그 후, 플로이드-워셜 알고리즘 (각 노드가 중간 노드일 때, 최소값 구하기)을 이용하여 최단거리를 구해나간다.
이때, 시작 노드(i)에서 중간 노드(k)까지의 연결이 되어 있지 않으면(map[i][k] == 0), 다음 단계로 건너뛴다.
만약, 그렇지 않다면, 중간 노드(k)와 도착 노드(j)까지의 연결을 확인한다.
이때, 중간 노드(k)와 도착 노드(j)가 연결되어 있지 않으면(map [k][j] ==0), 다음 단계로 건너뛴다.
(시작 노드와 도착 노드가 일치하는 경우(모두 0이다) 또한, 건너뛴다)
두 조건을 모두 만족한 경우에는 값을 업데이트시켜야 한다. 중간 노드를 거쳐 다른 노드까지의 접근이 더 빠르거나, 아직 업데이트를 하지 않은 경우(map [i][j] == 0)가 있다.
두 경우 모두 map [i][j]를 map [i][k]+map [k][j]의 값으로 업데이트한다.
이렇게 하면 정답을 구할 수 있다.
