문제 설명
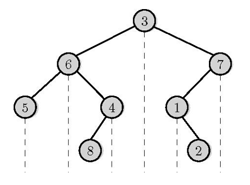
이진 트리는 매우 중요한 기본 자료 구조이다. 아래 그림은 루트 노드가 유일한 이진 트리이다. 모든 노드는 최대 2개의 자식 노드를 가질 수 있으며, 왼쪽 자식이 순서가 먼저이다. 노드 n개로 이루어진 이진 트리를 BT라고 하자. BT의 노드는 1부터 n까지 유일한 번호가 매겨져 있다.
아래 그림에 나와있는 BT의 루트는 3번 노드이다. 1번 노드는 오른쪽 자식만 가지고 있고, 4와 7은 왼쪽 자식만 가지고 있다. 3과 6은 왼쪽과 오른쪽 자식을 모두 가지고 있다. 나머지 노드는 모두 자식이 없으며, 이러한 노드는 리프 노드라고 부른다.
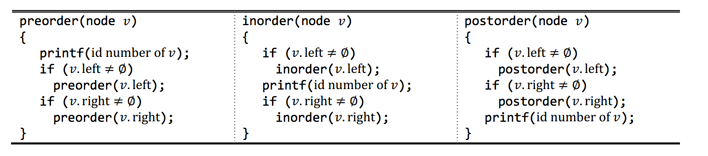
BT의 모든 노드를 순회하는 방법은 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder)로 총 세 가지가 있다. 이 세 방법은 아래에 C 스타일의 의사 코드로 나와 있다. BT의 노드 v에 대해서, v.left는 왼쪽 자식, v.right는 오른쪽 자식을 나타낸다. v가 왼쪽 자식이 없으면 v.left는 ∅와 같고, 오른쪽 자식이 없으면 v.right는 ∅와 같다.
BT를 전위 순회, 중위 순회한 결과가 주어진다. 즉, 위의 함수 중 preorder(root node of BT)와 inorder(root node of BT)를 호출해서 만든 리스트가 주어진다. 두 순회한 결과를 가지고 다시 BT를 만들 수 있다. BT의 전위, 중위 순회한 결과가 주어졌을 때, 후위 순회했을 때의 결과를 구하는 프로그램을 작성하시오.
예를 들어, 위의 그림을 전위 순회하면 3,6,5,4,8,7,1,2, 중위 순회하면 5,6,8,4,3,1,2,7이 된다. 이를 이용해 후위 순회하면 5,8,4,6,2,1,7,3이 된다.
제한 사항

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 노드의 개수 n이 주어진다. (1 ≤ n ≤ 1,000) BT의 모든 노드에는 1부터 n까지 서로 다른 번호가 매겨져 있다. 다음 줄에는 BT를 전위 순회한 결과, 그 다음 줄에는 중위 순회한 결과가 주어진다. 항상 두 순회 결과로 유일한 이진 트리가 만들어지는 경우만 입력으로 주어진다.
풀이
문제를 요약하면, 이진 트리의 전위, 중위 순회의 결과가 입력으로 들어온다면 후위 순회의 결과를 출력하는 것이다.
이진 트리의 순회의 특징을 분석하면 문제를 쉽게 풀 수 있다.
전위 순회는 루트를 가장 먼저 순회한다.
즉, 먼저 등장하는 노드가 더 위에 존재한다.
중위 순회는 왼쪽 자식노드를 가장 먼저 순회한다.
즉, 먼저 등장하는 노드가 더 왼쪽에 존재한다.
이 두 가지 특징을 이용하여 문제를 풀 수 있다.
전위 순회의 노드를 순서대로 선택하여 서브 트리의 루트로 볼 수 있다.
또한, 이 서브 트리의 루트를 중위 순회에서 찾으면 왼쪽과 오른쪽 서브 트리를 구할 수 있다.
예를 들어, 다음과 같은 입력이 들어왔다고 가정해 보자.
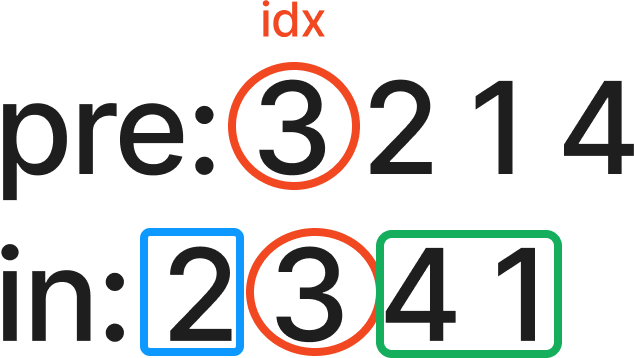
전위 순회에서 가장 먼저 등장한 3은 이 트리의 루트 노드이다.
3을 중위 순회에서 찾은 뒤, 먼저 등장한 노드들은 3의 왼쪽, 나중에 등장하는 노드들은 오른쪽 서브 트리에 속한다.
왼쪽과 오른쪽 서브 트리를 나눴다면 이를 재귀적으로 실행하면 된다.
이때, 전위, 중위 순회 모두 루트 노드를 기준으로 나눌 수 있다.
즉, 중위 순회에서 구분한 오른쪽 서브 트리는 전위 순회에서도 루트 이전의 인덱스를 갖지 못한다.
전위 순회에서 자신의 부모보다 일찍 등장할 수 없기 때문이다.
따라서, 오른쪽 서브 트리를 재귀적으로 구분할 때, 시작점을 서브 트리의 루트노드 다음으로 넘길 수 있다.
PostOrder(start, i, idx + 1, PreOrder, InOrder);
PostOrder(i+1, end, idx + 1 + i - start, PreOrder, InOrder);
결과적으로, 후위 순회의 결과를 출력해야 하기 때문에 양쪽 서브 트리의 순회를 마친 후 루트를 출력하면 된다.
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
void PostOrder(int start, int end, int idx, vector<int>& PreOrder, vector<int>& InOrder)
{
for (int i = start; i < end; i++)
{
if (PreOrder[idx] == InOrder[i])
{
PostOrder(start, i, idx + 1, PreOrder, InOrder);
PostOrder(i+1, end, idx + 1 + i - start, PreOrder, InOrder);
cout << PreOrder[idx] << " ";
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T, N;
cin >> T;
while (T-- > 0)
{
cin >> N;
vector<int> PreOrder(N);
vector<int> InOrder(N);
for (int i = 0; i < N; i++)
{
cin >> PreOrder[i];
}
for (int i = 0; i < N; i++)
{
cin >> InOrder[i];
}
PostOrder(0, N, 0, PreOrder, InOrder);
cout << "\n";
}
return 0;
}
문제 설명
이진 트리는 매우 중요한 기본 자료 구조이다. 아래 그림은 루트 노드가 유일한 이진 트리이다. 모든 노드는 최대 2개의 자식 노드를 가질 수 있으며, 왼쪽 자식이 순서가 먼저이다. 노드 n개로 이루어진 이진 트리를 BT라고 하자. BT의 노드는 1부터 n까지 유일한 번호가 매겨져 있다.
아래 그림에 나와있는 BT의 루트는 3번 노드이다. 1번 노드는 오른쪽 자식만 가지고 있고, 4와 7은 왼쪽 자식만 가지고 있다. 3과 6은 왼쪽과 오른쪽 자식을 모두 가지고 있다. 나머지 노드는 모두 자식이 없으며, 이러한 노드는 리프 노드라고 부른다.

BT의 모든 노드를 순회하는 방법은 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder)로 총 세 가지가 있다. 이 세 방법은 아래에 C 스타일의 의사 코드로 나와 있다. BT의 노드 v에 대해서, v.left는 왼쪽 자식, v.right는 오른쪽 자식을 나타낸다. v가 왼쪽 자식이 없으면 v.left는 ∅와 같고, 오른쪽 자식이 없으면 v.right는 ∅와 같다.

BT를 전위 순회, 중위 순회한 결과가 주어진다. 즉, 위의 함수 중 preorder(root node of BT)와 inorder(root node of BT)를 호출해서 만든 리스트가 주어진다. 두 순회한 결과를 가지고 다시 BT를 만들 수 있다. BT의 전위, 중위 순회한 결과가 주어졌을 때, 후위 순회했을 때의 결과를 구하는 프로그램을 작성하시오.
예를 들어, 위의 그림을 전위 순회하면 3,6,5,4,8,7,1,2, 중위 순회하면 5,6,8,4,3,1,2,7이 된다. 이를 이용해 후위 순회하면 5,8,4,6,2,1,7,3이 된다.
제한 사항

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 노드의 개수 n이 주어진다. (1 ≤ n ≤ 1,000) BT의 모든 노드에는 1부터 n까지 서로 다른 번호가 매겨져 있다. 다음 줄에는 BT를 전위 순회한 결과, 그 다음 줄에는 중위 순회한 결과가 주어진다. 항상 두 순회 결과로 유일한 이진 트리가 만들어지는 경우만 입력으로 주어진다.
풀이
문제를 요약하면, 이진 트리의 전위, 중위 순회의 결과가 입력으로 들어온다면 후위 순회의 결과를 출력하는 것이다.
이진 트리의 순회의 특징을 분석하면 문제를 쉽게 풀 수 있다.
전위 순회는 루트를 가장 먼저 순회한다.
즉, 먼저 등장하는 노드가 더 위에 존재한다.
중위 순회는 왼쪽 자식노드를 가장 먼저 순회한다.
즉, 먼저 등장하는 노드가 더 왼쪽에 존재한다.
이 두 가지 특징을 이용하여 문제를 풀 수 있다.
전위 순회의 노드를 순서대로 선택하여 서브 트리의 루트로 볼 수 있다.
또한, 이 서브 트리의 루트를 중위 순회에서 찾으면 왼쪽과 오른쪽 서브 트리를 구할 수 있다.
예를 들어, 다음과 같은 입력이 들어왔다고 가정해 보자.
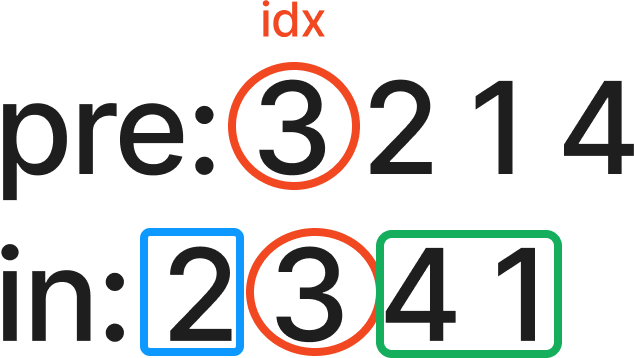
전위 순회에서 가장 먼저 등장한 3은 이 트리의 루트 노드이다.
3을 중위 순회에서 찾은 뒤, 먼저 등장한 노드들은 3의 왼쪽, 나중에 등장하는 노드들은 오른쪽 서브 트리에 속한다.
왼쪽과 오른쪽 서브 트리를 나눴다면 이를 재귀적으로 실행하면 된다.
이때, 전위, 중위 순회 모두 루트 노드를 기준으로 나눌 수 있다.
즉, 중위 순회에서 구분한 오른쪽 서브 트리는 전위 순회에서도 루트 이전의 인덱스를 갖지 못한다.
전위 순회에서 자신의 부모보다 일찍 등장할 수 없기 때문이다.
따라서, 오른쪽 서브 트리를 재귀적으로 구분할 때, 시작점을 서브 트리의 루트노드 다음으로 넘길 수 있다.
PostOrder(start, i, idx + 1, PreOrder, InOrder);
PostOrder(i+1, end, idx + 1 + i - start, PreOrder, InOrder);
결과적으로, 후위 순회의 결과를 출력해야 하기 때문에 양쪽 서브 트리의 순회를 마친 후 루트를 출력하면 된다.
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
void PostOrder(int start, int end, int idx, vector<int>& PreOrder, vector<int>& InOrder)
{
for (int i = start; i < end; i++)
{
if (PreOrder[idx] == InOrder[i])
{
PostOrder(start, i, idx + 1, PreOrder, InOrder);
PostOrder(i+1, end, idx + 1 + i - start, PreOrder, InOrder);
cout << PreOrder[idx] << " ";
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T, N;
cin >> T;
while (T-- > 0)
{
cin >> N;
vector<int> PreOrder(N);
vector<int> InOrder(N);
for (int i = 0; i < N; i++)
{
cin >> PreOrder[i];
}
for (int i = 0; i < N; i++)
{
cin >> InOrder[i];
}
PostOrder(0, N, 0, PreOrder, InOrder);
cout << "\n";
}
return 0;
}
