문제 설명
농부 존은 최근에 N × N개의 방이 있는 거대한 헛간을 새로 지었다. 각 방은 (1, 1)부터 (N,N)까지 번호가 매겨져있다(2 ≤ N ≤ 100). 어둠을 무서워하는 암소 베시는 최대한 많은 방에 불을 밝히고 싶어한다.
베시는 유일하게 불이 켜져있는 방인 (1, 1)방에서 출발한다. 어떤 방에는 다른 방의 불을 끄고 켤 수 있는 스위치가 달려있다. 예를 들어, (1, 1)방에 있는 스위치로 (1, 2)방의 불을 끄고 켤 수 있다. 베시는 불이 켜져있는 방으로만 들어갈 수 있고, 각 방에서는 상하좌우에 인접한 방으로 움직일 수 있다.
베시가 불을 켤 수 있는 방의 최대 개수를 구하시오.
제한 사항

첫 번째 줄에는 N(2 ≤ N ≤ 100)과, M(1 ≤ M ≤ 20,000)이 정수로 주어진다.
다음 M줄에는 네 개의 정수 x, y, a, b가 주어진다. (x, y)방에서 (a, b)방의 불을 켜고 끌 수 있다는 의미이다. 한 방에 여러개의 스위치가 있을 수 있고, 하나의 불을 조절하는 스위치 역시 여러개 있을 수 있다.
풀이
문제를 요약하면, 암소 베시는 불이 켜진 방에만 들어갈 수 있고, 각 방에는 다른 방의 불을 킬 수 있는 스위치가 존재한다.
베시는 최대한 많은 방의 불을 켜야 한다.
이 문제의 걸림돌은 스위치가 근접한 방의 불을 켜는 것이 아니라는 것이다.
즉, 어떠한 방을 먼저 방문하냐에 따라 불을 켤 수 있는 방의 개수가 달라진다.
예시를 보면 다음과 같은 상황이 된다.
//입력
5 9
1 1 1 2
1 2 1 3
1 3 1 4
1 4 1 5
1 5 2 1
2 1 2 5
2 5 3 1
3 5 3 1
2 3 3 5BFS를 통해 이동한다고 가정해 보자.
시작 상황은 다음과 같다.
노란색은 불이 켜진 방이고 연두색은 방문할 후보들을 나타낸다.
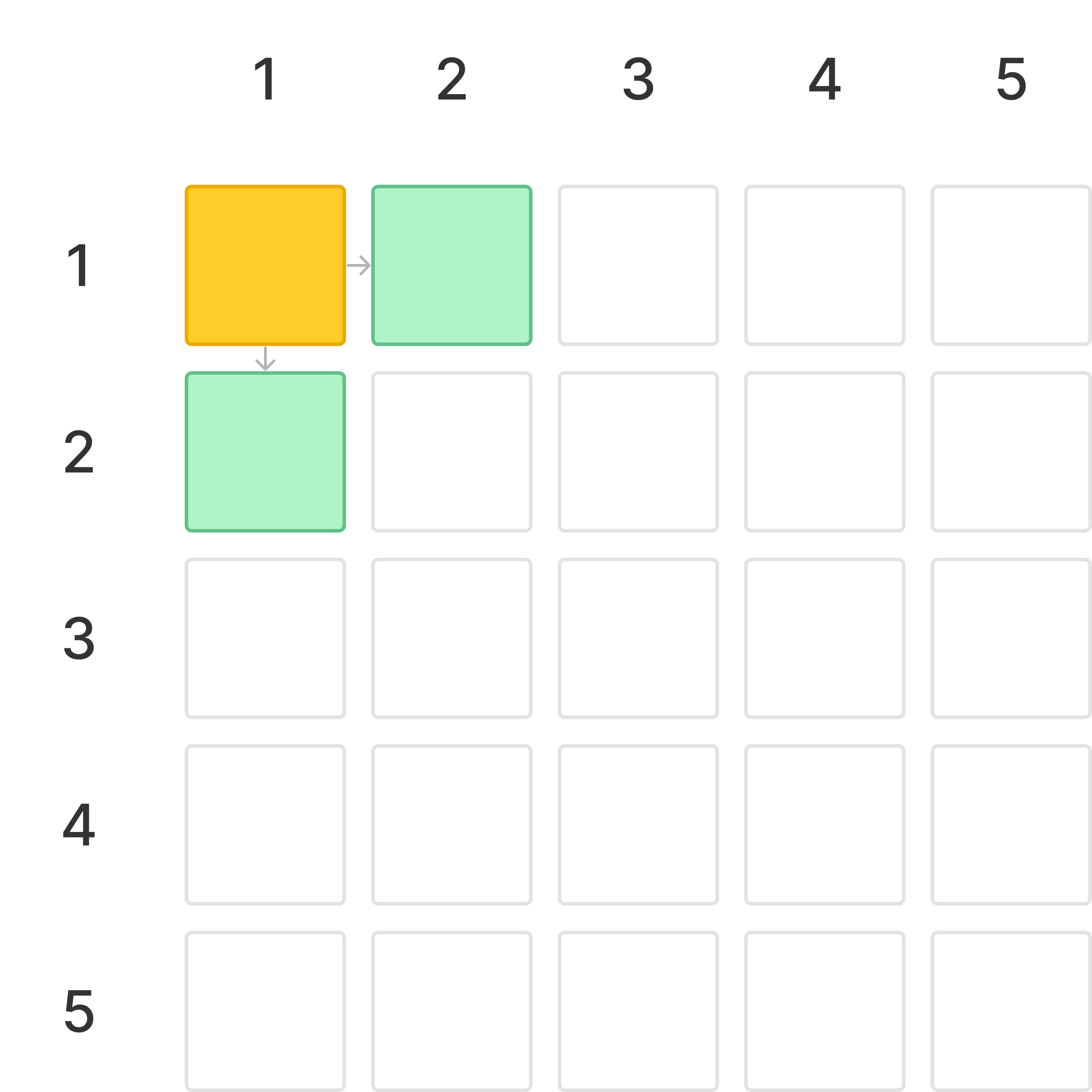
BFS를 통해 방을 순회하면 {1,2}에 들어가 {1,3}의 불을 킬 수 있다.
하지만, {2,1}은 불이 켜져있지 않아 이동할 수 없다.
이후 순서대로 방을 이동하여 다음과 같은 상황이 된다.
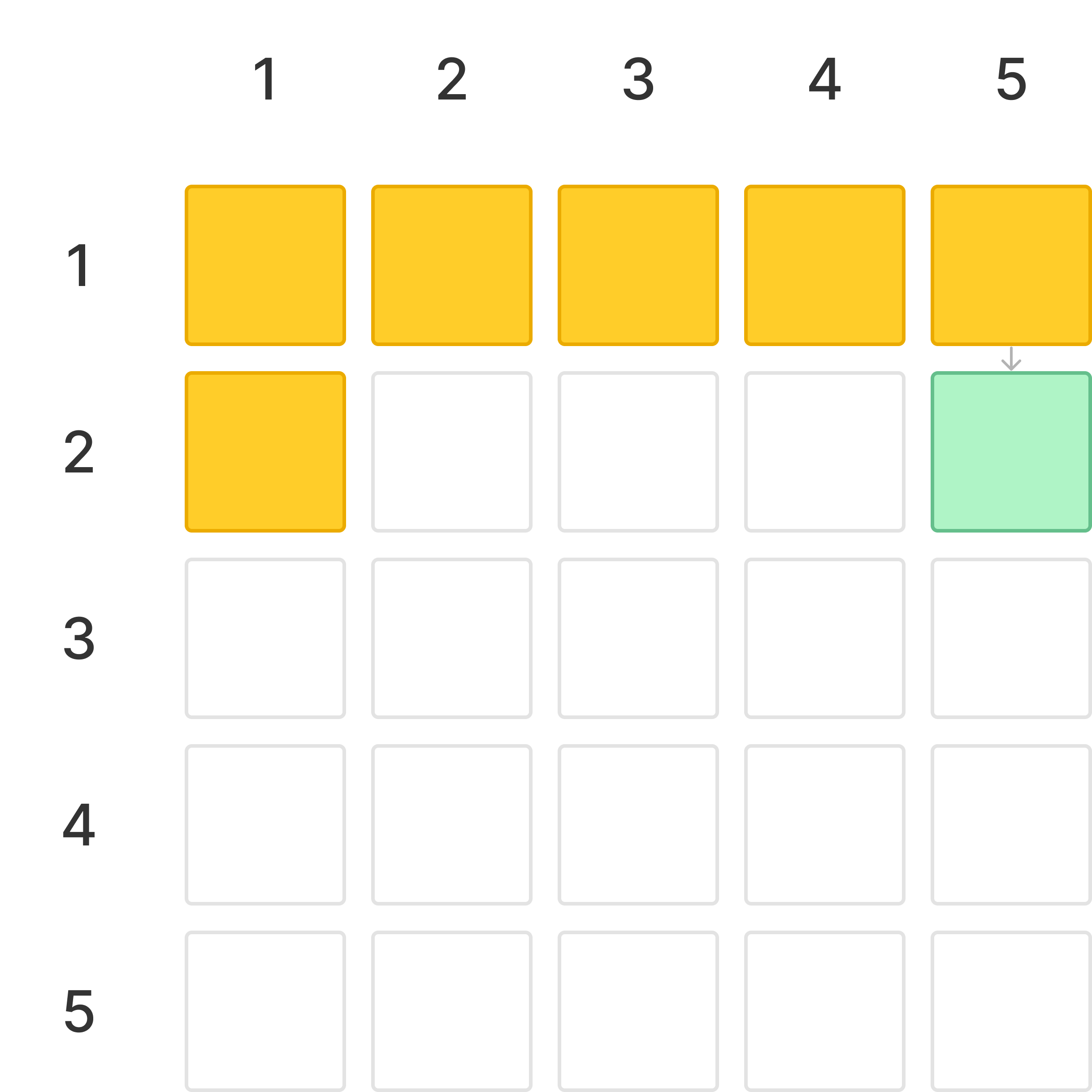
여기서 {2,5}는 불이 켜져 있지 않아 방문할 수 없다.
하지만, {2,1}의 불을 새로 켰기 때문에 더 방문할 방들이 남아 있지만, {1,1}을 방문했을 때는 불이 켜져있지 않아 큐에 추가하지 않았다.
즉, 방문한 방이라도 불이 새로 켜지면 다시 방문해야 한다.
다시 방문하는 방법은 간단하다.
불이 켜진 방의 인접한 방들을 방문한 적이 있다면 다시 방문할 수 있다는 뜻이다.
즉, 불이 켜질 때 인접한 방들을 탐색하여 다시 방문할지 여부를 체크하여 큐에 집어넣으면 된다.
for (auto [lightY, lightX] : Lights[y][x])
{
if (LightOn[lightY][lightX]) continue;
LightOn[lightY][lightX] = true;
result++;
for (int i = 0; i < 4; i++)
{
int prevY = lightY + dy[i];
int prevX = lightX + dx[i];
if (prevY < 0 || prevY >= N || prevX < 0 || prevX >= N) continue;
if (visited[prevY][prevX]) q.push({ prevY, prevX });
}
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
int BFS(vector<vector<vector<pair<int, int>>>>& Lights)
{
int result = 0;
queue<pair<int, int>> q;
q.push({ 0,0 });
vector<vector<bool>> LightOn(N, vector<bool>(N, false));
vector<vector<bool>> visited(N, vector<bool>(N, false));
LightOn[0][0] = true;
result++;
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
while (!q.empty())
{
auto [y, x] = q.front();
q.pop();
for (auto [lightY, lightX] : Lights[y][x])
{
if (LightOn[lightY][lightX]) continue;
LightOn[lightY][lightX] = true;
result++;
for (int i = 0; i < 4; i++)
{
int prevY = lightY + dy[i];
int prevX = lightX + dx[i];
if (prevY < 0 || prevY >= N || prevX < 0 || prevX >= N) continue;
if (visited[prevY][prevX]) q.push({ prevY, prevX });
}
}
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (!LightOn[newY][newX]) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
q.push({ newY,newX });
}
}
return result;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<vector<pair<int, int>>>> Lights(N, vector<vector<pair<int, int>>>(N));
for (int i = 0; i < M; i++)
{
int x, y, a, b;
cin >> y >> x >> a >> b;
Lights[y-1][x-1].push_back({ a-1,b-1 });
}
cout << BFS(Lights);
return 0;
}
문제 설명
농부 존은 최근에 N × N개의 방이 있는 거대한 헛간을 새로 지었다. 각 방은 (1, 1)부터 (N,N)까지 번호가 매겨져있다(2 ≤ N ≤ 100). 어둠을 무서워하는 암소 베시는 최대한 많은 방에 불을 밝히고 싶어한다.
베시는 유일하게 불이 켜져있는 방인 (1, 1)방에서 출발한다. 어떤 방에는 다른 방의 불을 끄고 켤 수 있는 스위치가 달려있다. 예를 들어, (1, 1)방에 있는 스위치로 (1, 2)방의 불을 끄고 켤 수 있다. 베시는 불이 켜져있는 방으로만 들어갈 수 있고, 각 방에서는 상하좌우에 인접한 방으로 움직일 수 있다.
베시가 불을 켤 수 있는 방의 최대 개수를 구하시오.
제한 사항

첫 번째 줄에는 N(2 ≤ N ≤ 100)과, M(1 ≤ M ≤ 20,000)이 정수로 주어진다.
다음 M줄에는 네 개의 정수 x, y, a, b가 주어진다. (x, y)방에서 (a, b)방의 불을 켜고 끌 수 있다는 의미이다. 한 방에 여러개의 스위치가 있을 수 있고, 하나의 불을 조절하는 스위치 역시 여러개 있을 수 있다.
풀이
문제를 요약하면, 암소 베시는 불이 켜진 방에만 들어갈 수 있고, 각 방에는 다른 방의 불을 킬 수 있는 스위치가 존재한다.
베시는 최대한 많은 방의 불을 켜야 한다.
이 문제의 걸림돌은 스위치가 근접한 방의 불을 켜는 것이 아니라는 것이다.
즉, 어떠한 방을 먼저 방문하냐에 따라 불을 켤 수 있는 방의 개수가 달라진다.
예시를 보면 다음과 같은 상황이 된다.
//입력
5 9
1 1 1 2
1 2 1 3
1 3 1 4
1 4 1 5
1 5 2 1
2 1 2 5
2 5 3 1
3 5 3 1
2 3 3 5BFS를 통해 이동한다고 가정해 보자.
시작 상황은 다음과 같다.
노란색은 불이 켜진 방이고 연두색은 방문할 후보들을 나타낸다.

BFS를 통해 방을 순회하면 {1,2}에 들어가 {1,3}의 불을 킬 수 있다.
하지만, {2,1}은 불이 켜져있지 않아 이동할 수 없다.
이후 순서대로 방을 이동하여 다음과 같은 상황이 된다.

여기서 {2,5}는 불이 켜져 있지 않아 방문할 수 없다.
하지만, {2,1}의 불을 새로 켰기 때문에 더 방문할 방들이 남아 있지만, {1,1}을 방문했을 때는 불이 켜져있지 않아 큐에 추가하지 않았다.
즉, 방문한 방이라도 불이 새로 켜지면 다시 방문해야 한다.
다시 방문하는 방법은 간단하다.
불이 켜진 방의 인접한 방들을 방문한 적이 있다면 다시 방문할 수 있다는 뜻이다.
즉, 불이 켜질 때 인접한 방들을 탐색하여 다시 방문할지 여부를 체크하여 큐에 집어넣으면 된다.
for (auto [lightY, lightX] : Lights[y][x])
{
if (LightOn[lightY][lightX]) continue;
LightOn[lightY][lightX] = true;
result++;
for (int i = 0; i < 4; i++)
{
int prevY = lightY + dy[i];
int prevX = lightX + dx[i];
if (prevY < 0 || prevY >= N || prevX < 0 || prevX >= N) continue;
if (visited[prevY][prevX]) q.push({ prevY, prevX });
}
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
int BFS(vector<vector<vector<pair<int, int>>>>& Lights)
{
int result = 0;
queue<pair<int, int>> q;
q.push({ 0,0 });
vector<vector<bool>> LightOn(N, vector<bool>(N, false));
vector<vector<bool>> visited(N, vector<bool>(N, false));
LightOn[0][0] = true;
result++;
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
while (!q.empty())
{
auto [y, x] = q.front();
q.pop();
for (auto [lightY, lightX] : Lights[y][x])
{
if (LightOn[lightY][lightX]) continue;
LightOn[lightY][lightX] = true;
result++;
for (int i = 0; i < 4; i++)
{
int prevY = lightY + dy[i];
int prevX = lightX + dx[i];
if (prevY < 0 || prevY >= N || prevX < 0 || prevX >= N) continue;
if (visited[prevY][prevX]) q.push({ prevY, prevX });
}
}
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (!LightOn[newY][newX]) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
q.push({ newY,newX });
}
}
return result;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<vector<pair<int, int>>>> Lights(N, vector<vector<pair<int, int>>>(N));
for (int i = 0; i < M; i++)
{
int x, y, a, b;
cin >> y >> x >> a >> b;
Lights[y-1][x-1].push_back({ a-1,b-1 });
}
cout << BFS(Lights);
return 0;
}