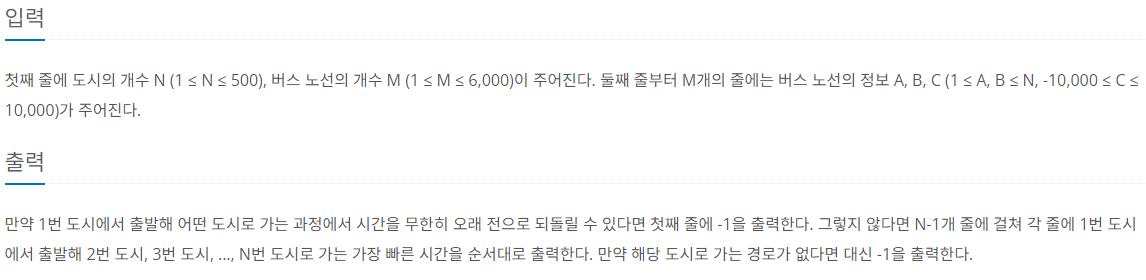
문제 설명
N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스가 M개 있다. 각 버스는 A, B, C로 나타낼 수 있는데, A는 시작도시, B는 도착도시, C는 버스를 타고 이동하는데 걸리는 시간이다. 시간 C가 양수가 아닌 경우가 있다. C = 0인 경우는 순간 이동을 하는 경우, C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우이다.
1번 도시에서 출발해서 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램을 작성하시오.
제한 사항

풀이
문제를 요약하면, 1번 노드에서 N개의 노드로의 최솟값을 구하는 문제이다.
전형적인 그래프 문제이지만, 해당 문제에서는 음수 간선을 포함한다.
즉, 다익스트라는 사용이 불가능하다.
다익스트라는 우선순위 큐의 요소들이 모두 없어질 때까지 동작한다.
하지만, 음수 사이클이 존재한다면 무한하게 간선이 추가되기 때문에 불가능하다.
따라서, 해당 문제는 벨만포드 알고리즘을 사용해야 한다.
벨만포드는 음수 간선이 가능하며 음수 사이클을 판단할 수 있다.
벨만포드는 다익스트라처럼 하나의 노드씩 판정하는게 아니라 라운드로 진행된다고 이해하면 쉽다.
한 번의 라운드에서 모든 간선을 통해 도달할 수 있는 노드의 거리를 업데이트하면 된다.
예를 들어 보자.
3 4
1 2 4
1 3 3
2 3 -1
3 1 -2첫 번째 라운드에서는 다음과 같이 된다.
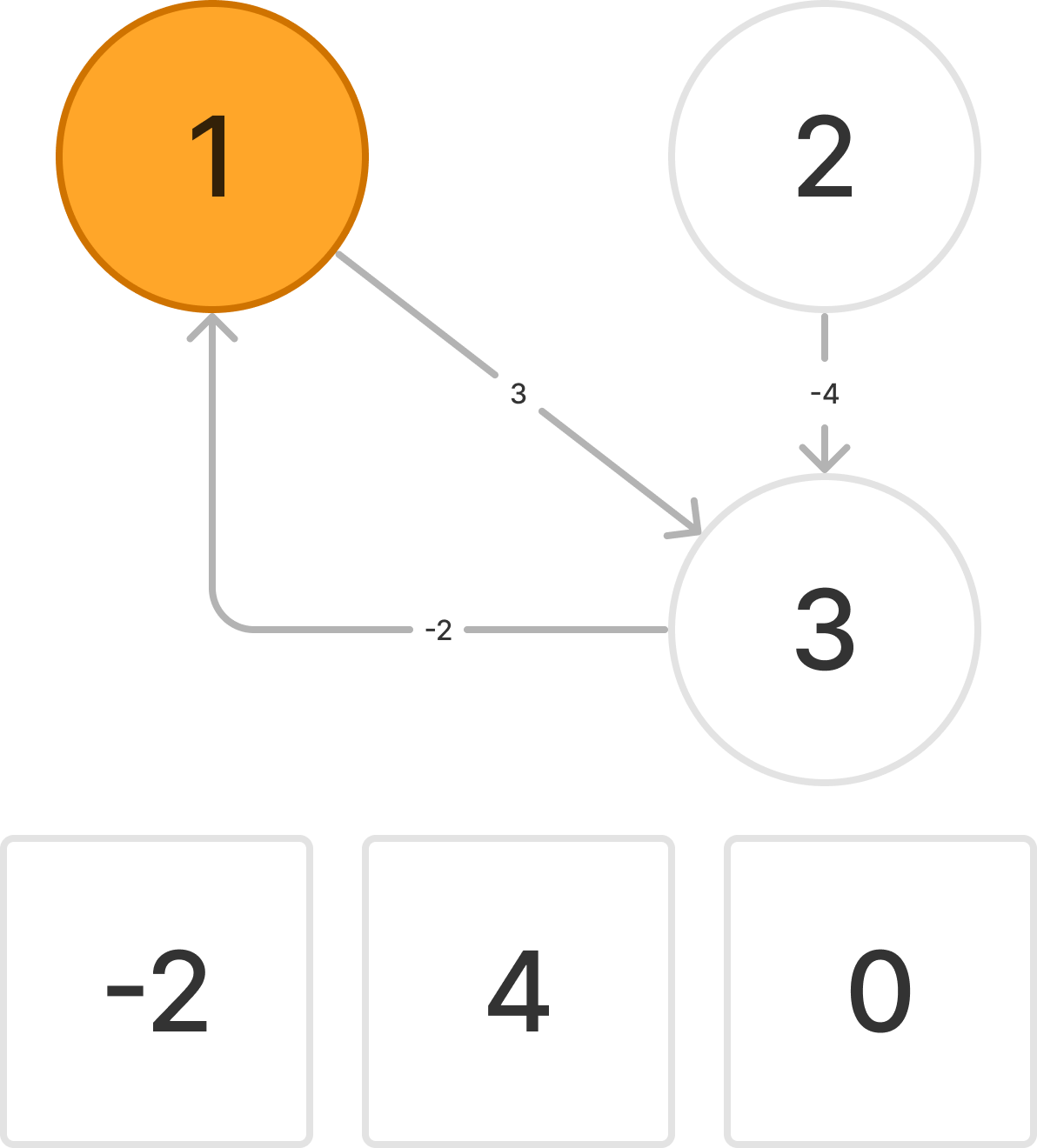
1 → 2 을 통해 2까지의 거리가 4로 업데이트된다.
1 → 3 을 통해 3까지의 거리가 3으로 업데이트된다.
2 → 3 을 통해 3까지의 거리가 3으로 업데이트할 수 있지만, 이미 같은 거리로 업데이트되어 있다.
3 → 1 을 통해 1까지의 거리가 -2로 업데이트된다.
bool bUpdated = false;
for (int i = 1; i <= N; i++)
{
bUpdated = false;
for (auto e : edges)
{
auto [a, b, c] = e;
if (Distance[a] == INT_MAX) continue;
if (Distance[b] > Distance[a] + c)
{
Distance[b] = Distance[a] + c;
bUpdated = true;
}
}
if (!bUpdated) break;
else if (i == N)
{
cout << -1;
return 0;
}
}
이를 N-1번의 라운드를 통해 거리를 업데이트한다.
N-1번 반복하는 이유는 최단 경로가 포함하는 간선의 수가 최대 N-1개이기 때문이다.
이후, 마지막으로 N번째 라운드를 진행하는데 만약 거리가 업데이트된다면 음수 사이클이 존재한다는 뜻이다.
다른 말로 무한하게 작아진다는 뜻이다.
문제에서는 이를 발견하면 -1을 출력하게끔 하였다.
한 가지 주의사항은 가중치와 간선의 개수가 최대로 클때는 int의 표현범위를 넘어가게 된다.
그래서 long long을 사용해야 한다.
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
long long N, M;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<tuple<int,int,int>> edges;
for (int i = 0; i < M; i++)
{
int A, B, C;
cin >> A >> B >> C;
edges.push_back({ A, B, C });
}
vector<long long> Distance(N + 1, INT_MAX);
Distance[1] = 0;
bool bUpdated = false;
for (int i = 1; i <= N; i++)
{
bUpdated = false;
for (auto e : edges)
{
auto [a, b, c] = e;
if (Distance[a] == INT_MAX) continue;
if (Distance[b] > Distance[a] + c)
{
Distance[b] = Distance[a] + c;
bUpdated = true;
}
}
if (!bUpdated) break;
else if (i == N)
{
cout << -1;
return 0;
}
}
for (int i = 2; i <= N; i++)
{
if (Distance[i] == INT_MAX) cout << -1 << "\n";
else cout << Distance[i] << "\n";
}
return 0;
}