문제 설명
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
- BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
제한 사항

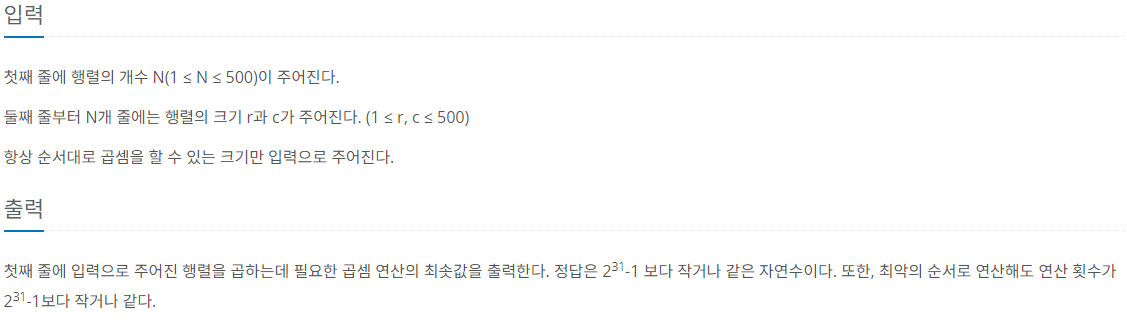
풀이
문제를 요약하면, 행렬의 곱셈의 순서를 적절히 조절하여 최소한의 연산의 횟수를 구해야 한다.
처음 문제를 풀었을 때, N이 500 이하이기 대문에 $O(N^2)$으로 문제를 풀어도 가능하다고 생각했다.
따라서, 백트래킹을 통해 행렬을 직접 계산해 봤다.
하지만, 시간초과가 발생했다.
시간을 줄이기 위해서는 DP를 사용해야 한다.
DP에서 유지할 값은 start부터 end까지의 최소 연산 횟수이다.
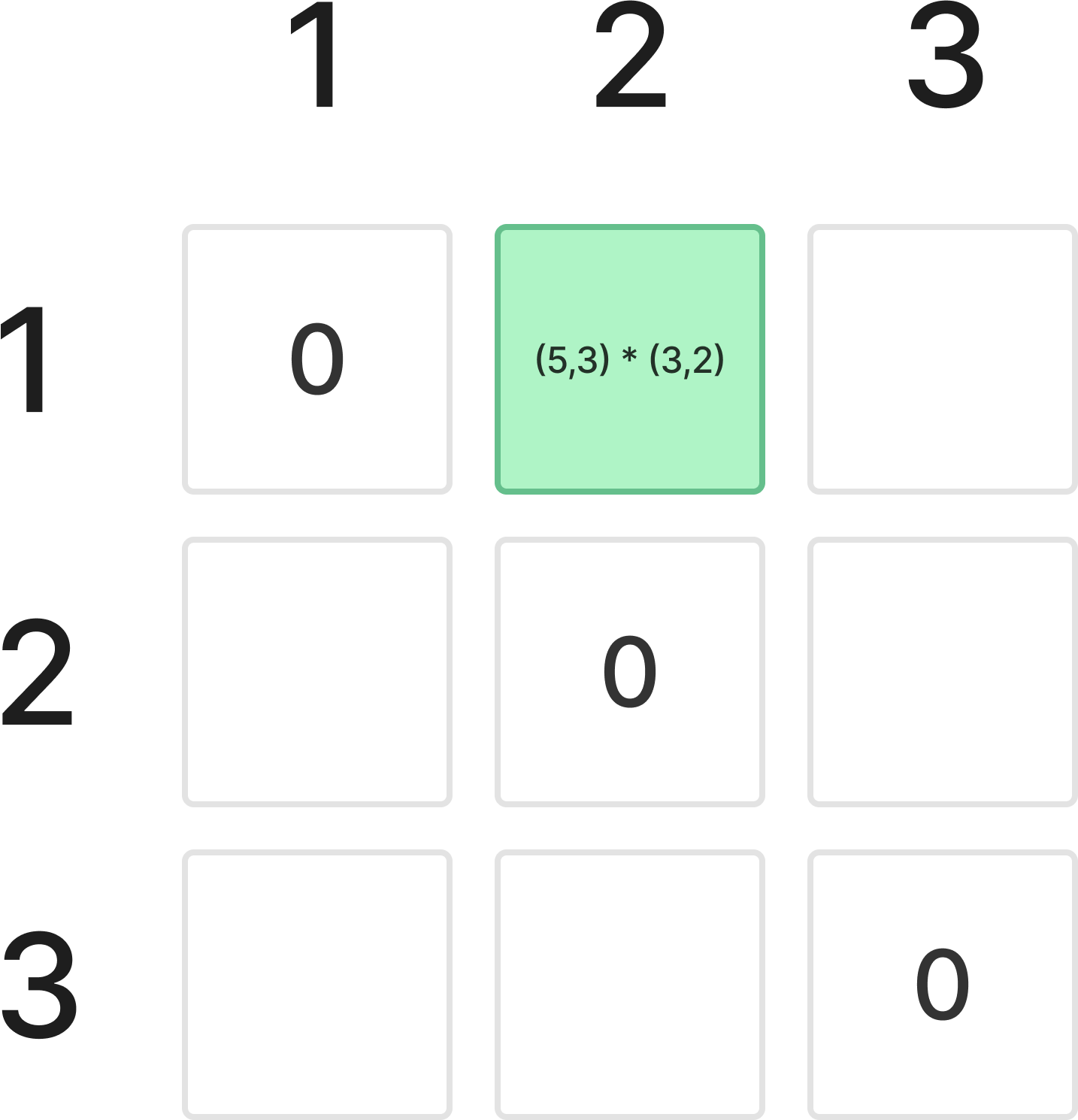
즉, 초록색 칸에 저장될 값은 1번부터 2번까지의 최소 연산 횟수이다.
따라서, 크기가 k인 행렬의 연산 횟수를 구하는 작업을 행렬의 시작위치를 달리하여 계산하면 된다.
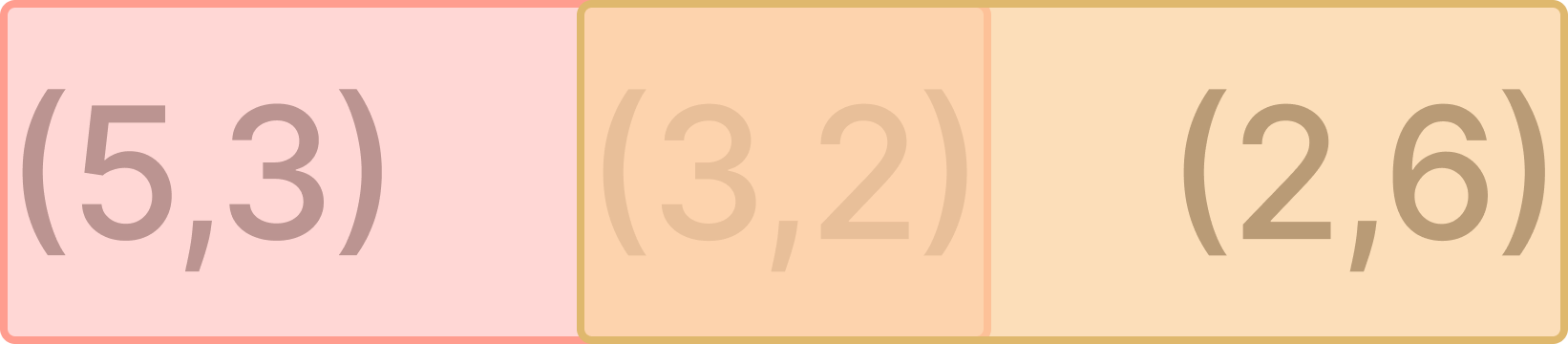
이렇게 계산한 결과는 다음과 같이 저장된다.
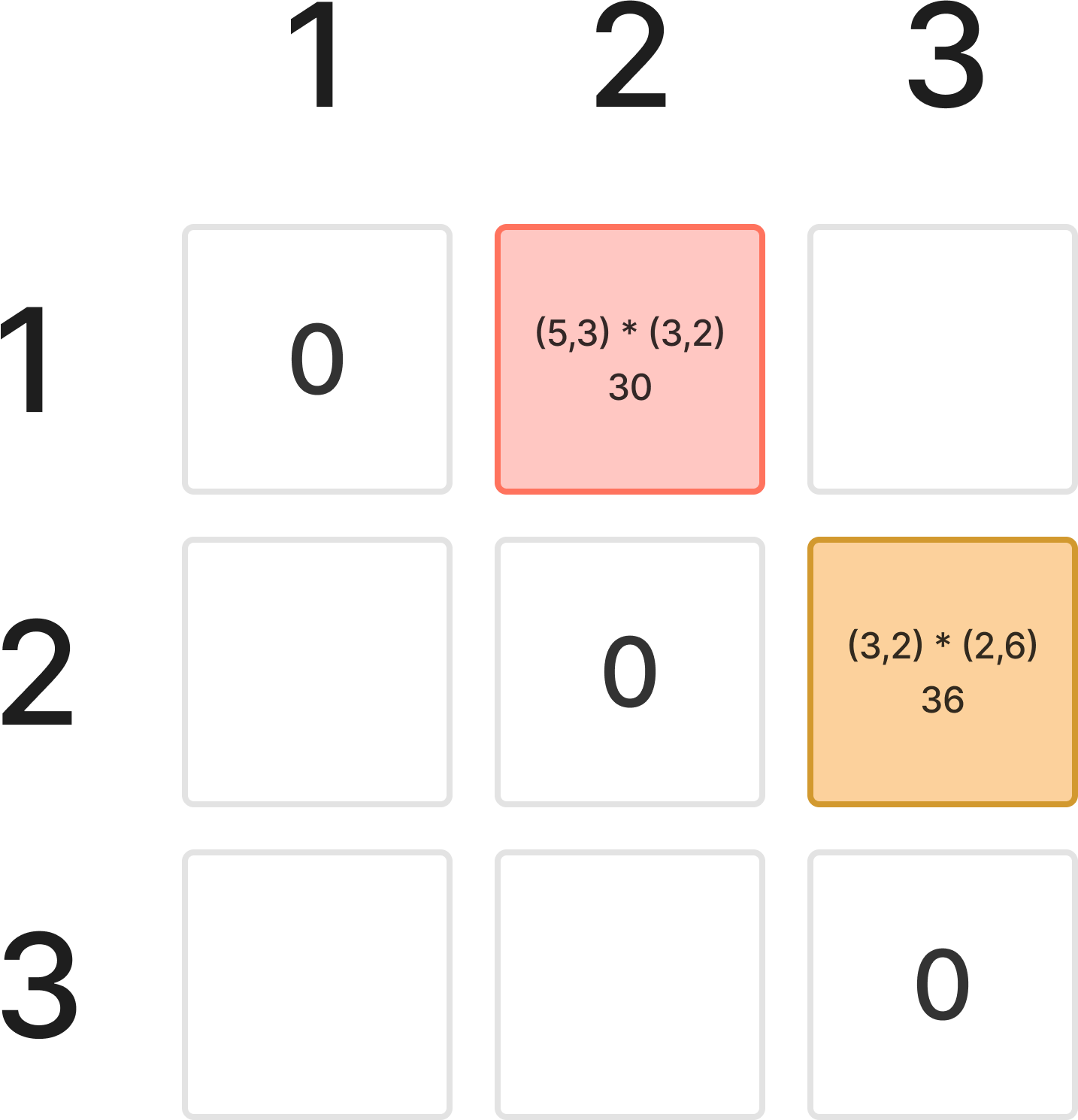
이후, 계산하려는 구간의 하나의 지점을 정하여 중간이 되었다고 가정하며 계산해야 한다.
예를 들어, ABCD의 결과를 구하기 위해서는 (AB)(CD)가 최소일 수도 있고 (ABC)D가 최소일 수도 있기 때문이다.
이때, DP에 저장된 값들이 활용된다.
(AB)(CD)를 구한다고 가정했을 때, (AB)의 값과 (CD)의 값은 이미 계산되어 DP에 있다.
따라서, (AB)의 결과와 (CD)의 결과를 곱하는 연산 횟수만 더해주면 된다.
이를 구하는 것은 간단하다.
int Sum(vector<pair<int, int>>& Matrices, int Start, int Mid, int End)
{
return Matrices[Start].first * Matrices[Mid].second * Matrices[End].second;
}
즉, 최종적인 연산은 다음과 같다.
DP[start][end] = min(DP[start][end], DP[start][mid] + DP[mid + 1][end] + Sum(Matrices, start, mid, end));
이렇게 계산하여 DP[0][N-1]의 값을 출력하면 된다.
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
int ans = INT_MAX;
int Sum(vector<pair<int, int>>& Matrices, int Start, int Mid, int End)
{
return Matrices[Start].first * Matrices[Mid].second * Matrices[End].second;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<pair<int, int>> Matrices;
vector<vector<int>> DP(N, vector<int>(N, INT_MAX));
for (int i = 0; i < N; i++)
{
int a, b;
cin >> a >> b;
Matrices.push_back({ a,b });
DP[i][i] = 0;
}
for (int k = 1; k < N; k++)
{
for (int start = 0; start+k < N; start++)
{
int end = start + k;
for (int mid = start; mid < end; mid++)
{
DP[start][end] = min(DP[start][end], DP[start][mid] + DP[mid + 1][end] + Sum(Matrices, start, mid, end));
}
}
}
cout << DP[0][N-1];
return 0;
}
문제 설명
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
- BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
제한 사항


풀이
문제를 요약하면, 행렬의 곱셈의 순서를 적절히 조절하여 최소한의 연산의 횟수를 구해야 한다.
처음 문제를 풀었을 때, N이 500 이하이기 대문에
따라서, 백트래킹을 통해 행렬을 직접 계산해 봤다.
하지만, 시간초과가 발생했다.
시간을 줄이기 위해서는 DP를 사용해야 한다.
DP에서 유지할 값은 start부터 end까지의 최소 연산 횟수이다.

즉, 초록색 칸에 저장될 값은 1번부터 2번까지의 최소 연산 횟수이다.
따라서, 크기가 k인 행렬의 연산 횟수를 구하는 작업을 행렬의 시작위치를 달리하여 계산하면 된다.
이렇게 계산한 결과는 다음과 같이 저장된다.

이후, 계산하려는 구간의 하나의 지점을 정하여 중간이 되었다고 가정하며 계산해야 한다.
예를 들어, ABCD의 결과를 구하기 위해서는 (AB)(CD)가 최소일 수도 있고 (ABC)D가 최소일 수도 있기 때문이다.
이때, DP에 저장된 값들이 활용된다.
(AB)(CD)를 구한다고 가정했을 때, (AB)의 값과 (CD)의 값은 이미 계산되어 DP에 있다.
따라서, (AB)의 결과와 (CD)의 결과를 곱하는 연산 횟수만 더해주면 된다.
이를 구하는 것은 간단하다.
int Sum(vector<pair<int, int>>& Matrices, int Start, int Mid, int End)
{
return Matrices[Start].first * Matrices[Mid].second * Matrices[End].second;
}
즉, 최종적인 연산은 다음과 같다.
DP[start][end] = min(DP[start][end], DP[start][mid] + DP[mid + 1][end] + Sum(Matrices, start, mid, end));
이렇게 계산하여 DP[0][N-1]의 값을 출력하면 된다.
전체 코드
#include <stdio.h>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
int ans = INT_MAX;
int Sum(vector<pair<int, int>>& Matrices, int Start, int Mid, int End)
{
return Matrices[Start].first * Matrices[Mid].second * Matrices[End].second;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<pair<int, int>> Matrices;
vector<vector<int>> DP(N, vector<int>(N, INT_MAX));
for (int i = 0; i < N; i++)
{
int a, b;
cin >> a >> b;
Matrices.push_back({ a,b });
DP[i][i] = 0;
}
for (int k = 1; k < N; k++)
{
for (int start = 0; start+k < N; start++)
{
int end = start + k;
for (int mid = start; mid < end; mid++)
{
DP[start][end] = min(DP[start][end], DP[start][mid] + DP[mid + 1][end] + Sum(Matrices, start, mid, end));
}
}
}
cout << DP[0][N-1];
return 0;
}