문제 설명
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
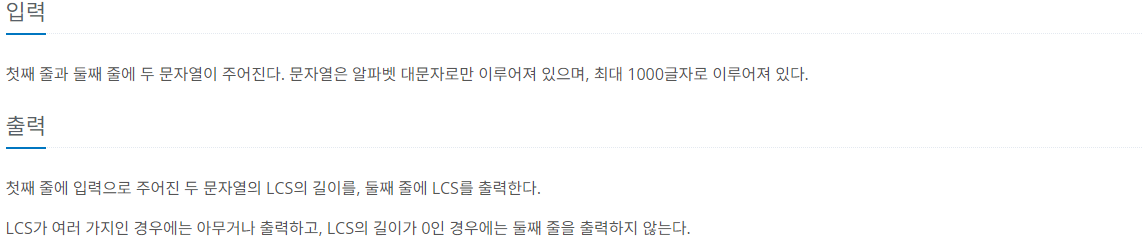
제한 사항

풀이
문제를 요약하면 LCS를 구하는 것이다.
LCS는 최장 공통 부분 수열을 의미한다.
최장 공통 부분 수열은 두 개의 문자열 혹은 배열에서 가장 긴 공통된 부분을 의미한다.
예를 들어 보자.
ACAYKP, CAPCAK 두 개의 문자열의 LCS는 ACAK이다.
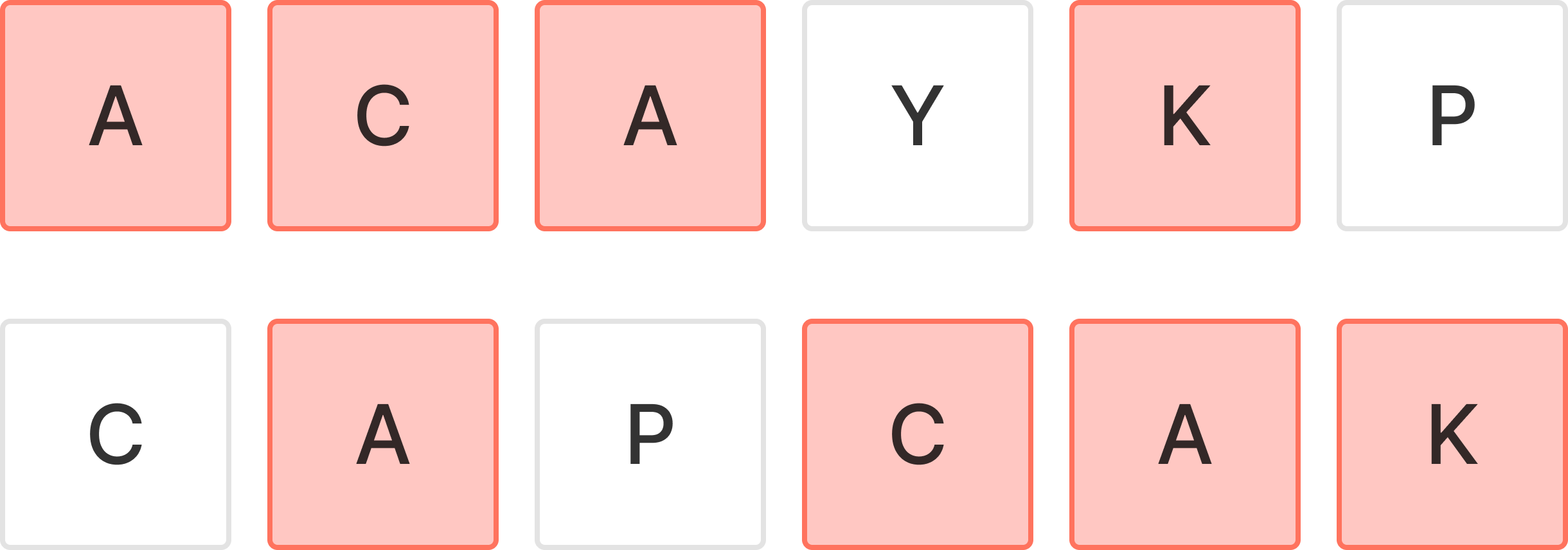
그렇다면, 이를 어떻게 구해내는지 알아보자.
LCS는 DP를 이용하여 간단하게 구해낼 수 있다.
이차원 배열을 통해 메모이제이션을 한다.
두 문자열의 각 위치를 비교하며 같을 때와 다를 때를 구분하여 처리한다.
만약, 두 요소가 같다면 이전 문자열에서 해당 요소를 추가한 것이 LCS가 될 것이다.
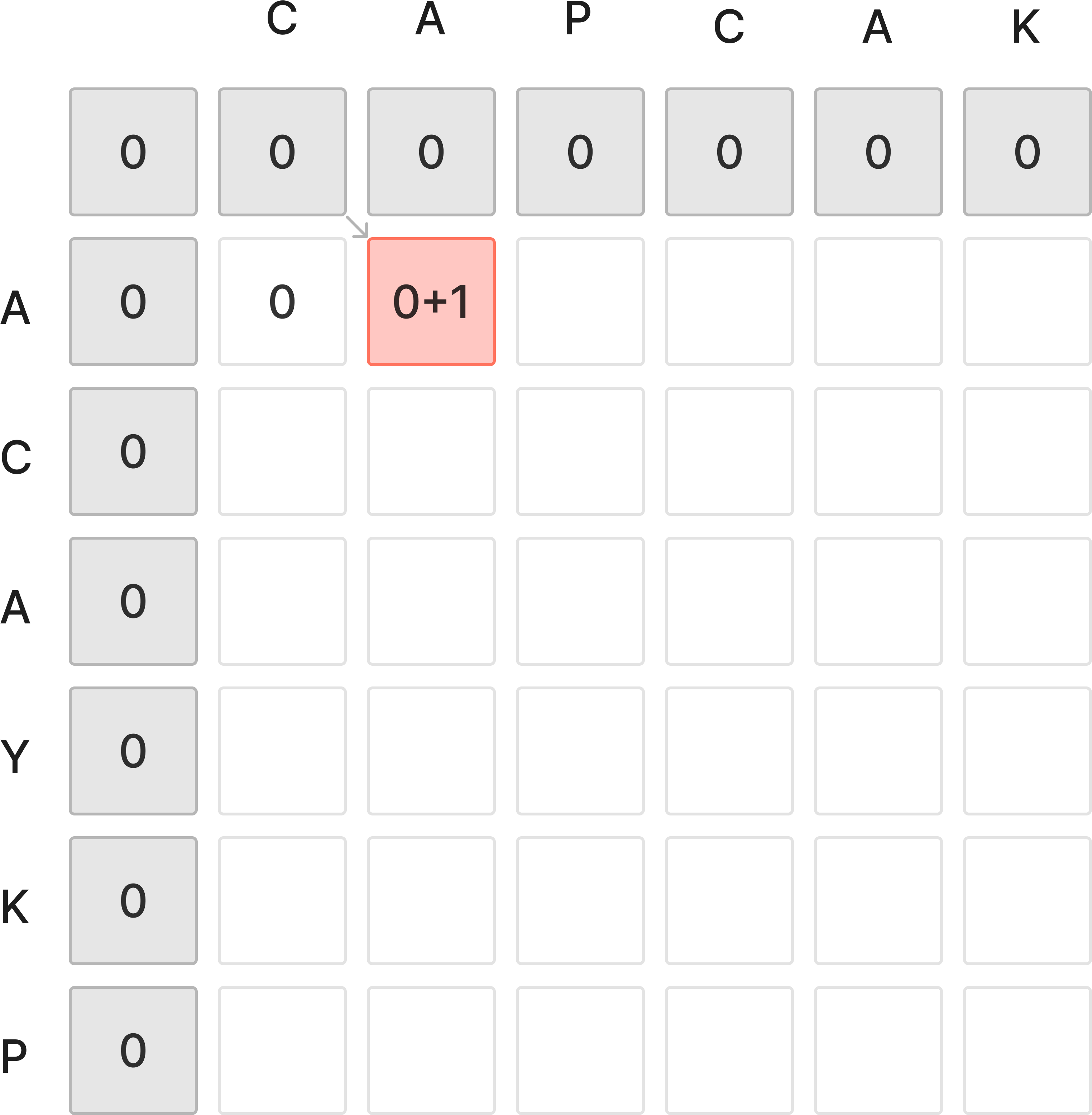
빨간 부분을 보면, A로 두 문자열이 공통 요소를 갖는다.
이는 이전 단계에서 구한 LCS에 A를 추가하여 얻는 것과 같은 결과이다.
물론 제일 처음 문자이기에 이전 단계가 없다.
회색으로 칠해진 부분은 계산을 용이하게 하기 위한 패딩이다.
하나의 상황을 더 보자.
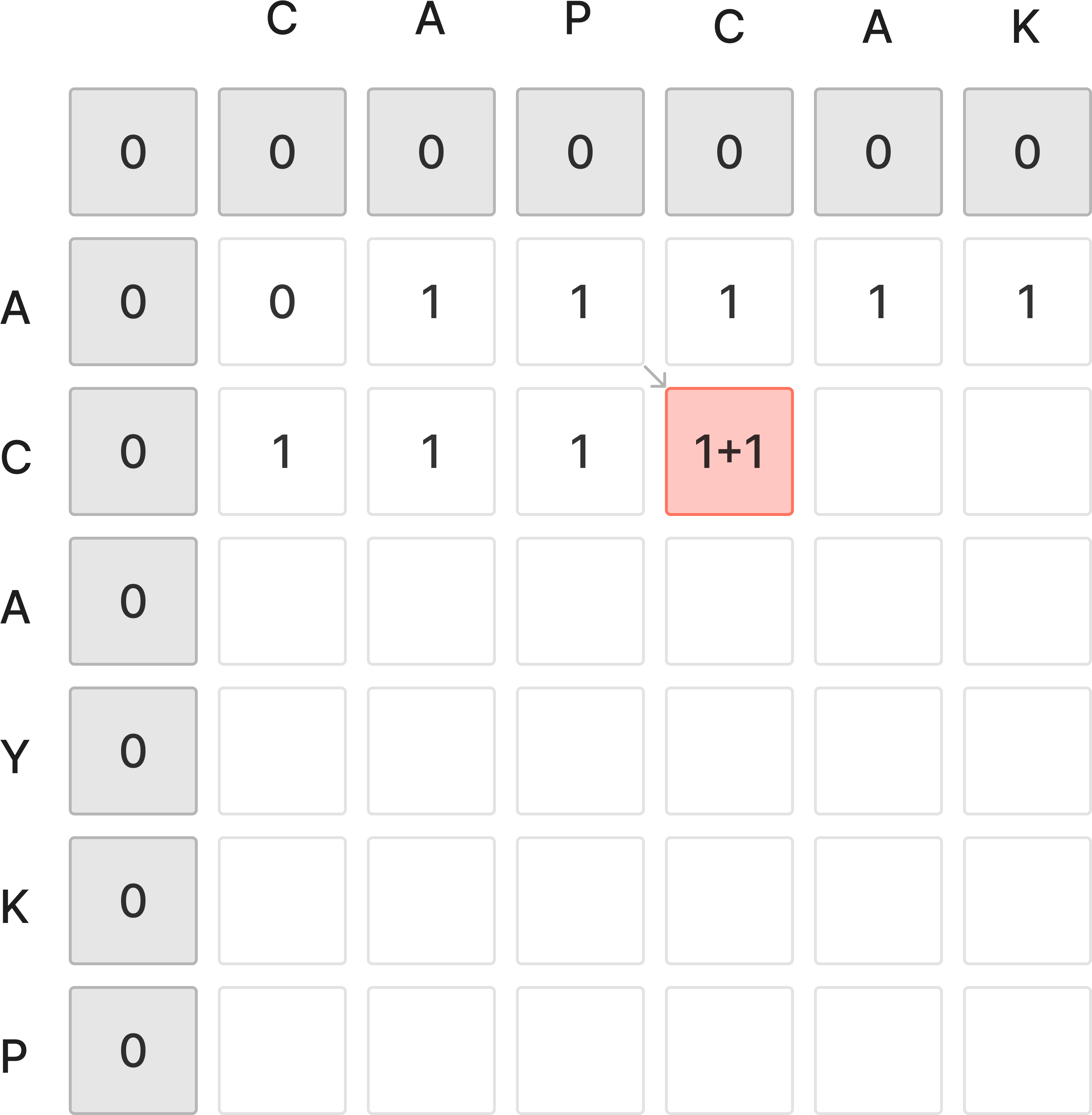
빨간 부분은 C가 두 문자열의 공통부분이 되는 상황이다.
C를 비교하는 상황의 문자열은 AC와 CAPC가 된다.
이 둘의 LCS는 AC이다.
즉, C이전에 찾은 LCS인 A에 C를 추가하여 만드는 상황이다.
따라서, dp[i-1][j-1]에 1을 추가한 것과 같다.
if(str1[i] == str2[j]) dp[i][j] = dp[i-1][j-1];
그럼 두 요소가 다른 경우는 어떤지 살펴보자.
두 요소가 다르다면 LCS는 이전에 만들어 놓은 LCS중 하나가 될 것이다.
이때, 두 가지 선택지가 있다.
str1에서 1개가 빠진 것이 최장 LCS일지 str2에서 1개가 빠진 것이 최장 LCS일지 모른다.
예를 들어 보자.
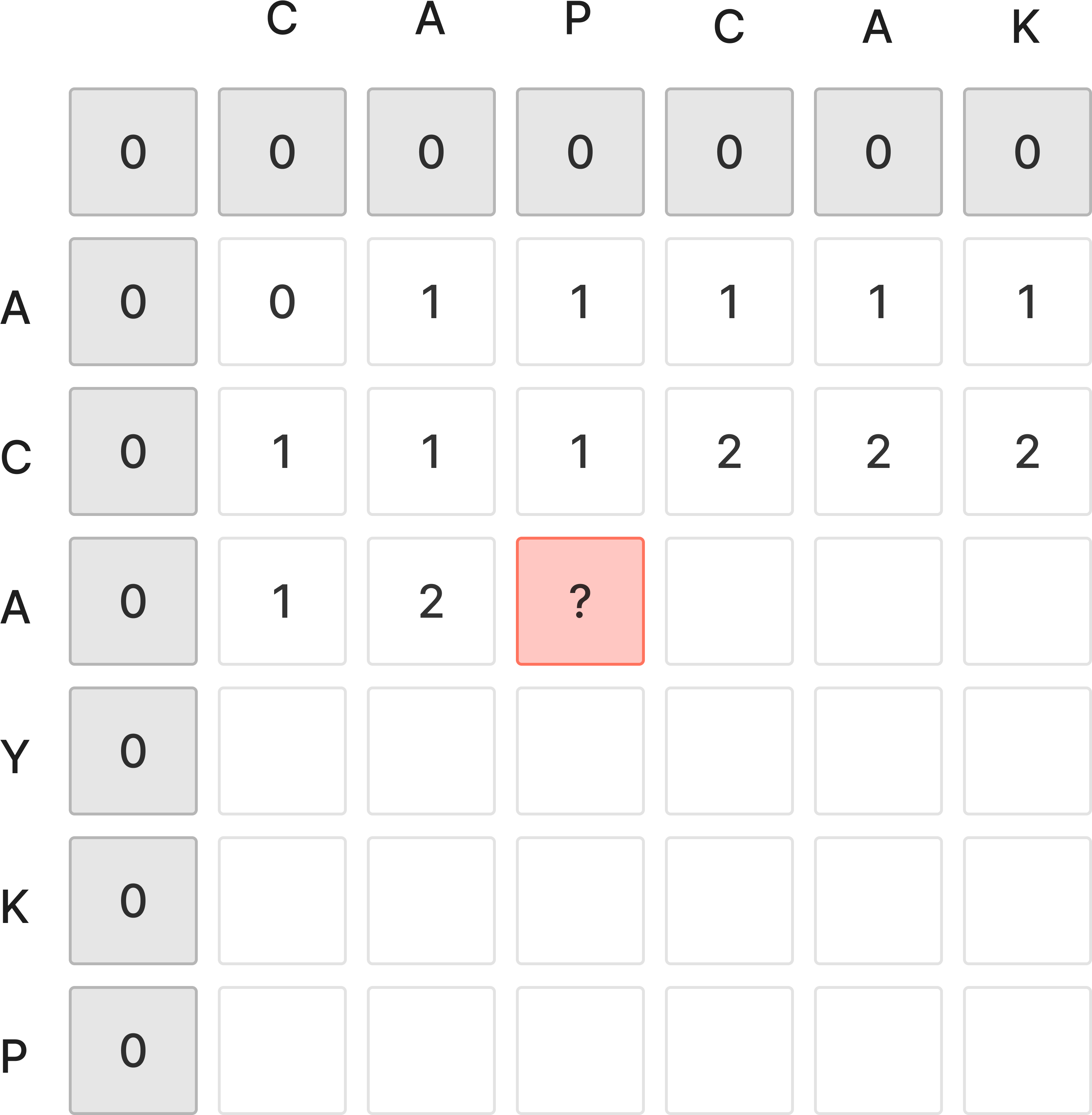
빨간 부분을 보면 ACA와 CAP를 비교하는 과정이다.
이때 A와 P는 다르기 때문에 이전에 찾아 놓은 LCS를 기록하려 한다.
[AC - CAP], [ACA - CA] 둘 중 더 긴 LCS를 골라야 한다.
- AC-CAP: A
- ACA-CA: CA
후자의 경우가 더 긴 LCS를 갖고 있다.
이를 식으로 정리해 보면 다음과 같다.
if(str1[i] != str2[j]) dp[i][j] = max(dp[i-1][j], dp[i][j-1]);이렇게 모든 문자열을 탐색하면 최장 LCS의 길이를 구해낼 수 있다.
그렇다면, 최장 LCS가 갖는 요소들을 찾아내야 한다.
이 역시 간단한 방법으로 구할 수 있다.
메모이제이션을 모두 완료하면 다음과 같은 상황이다.
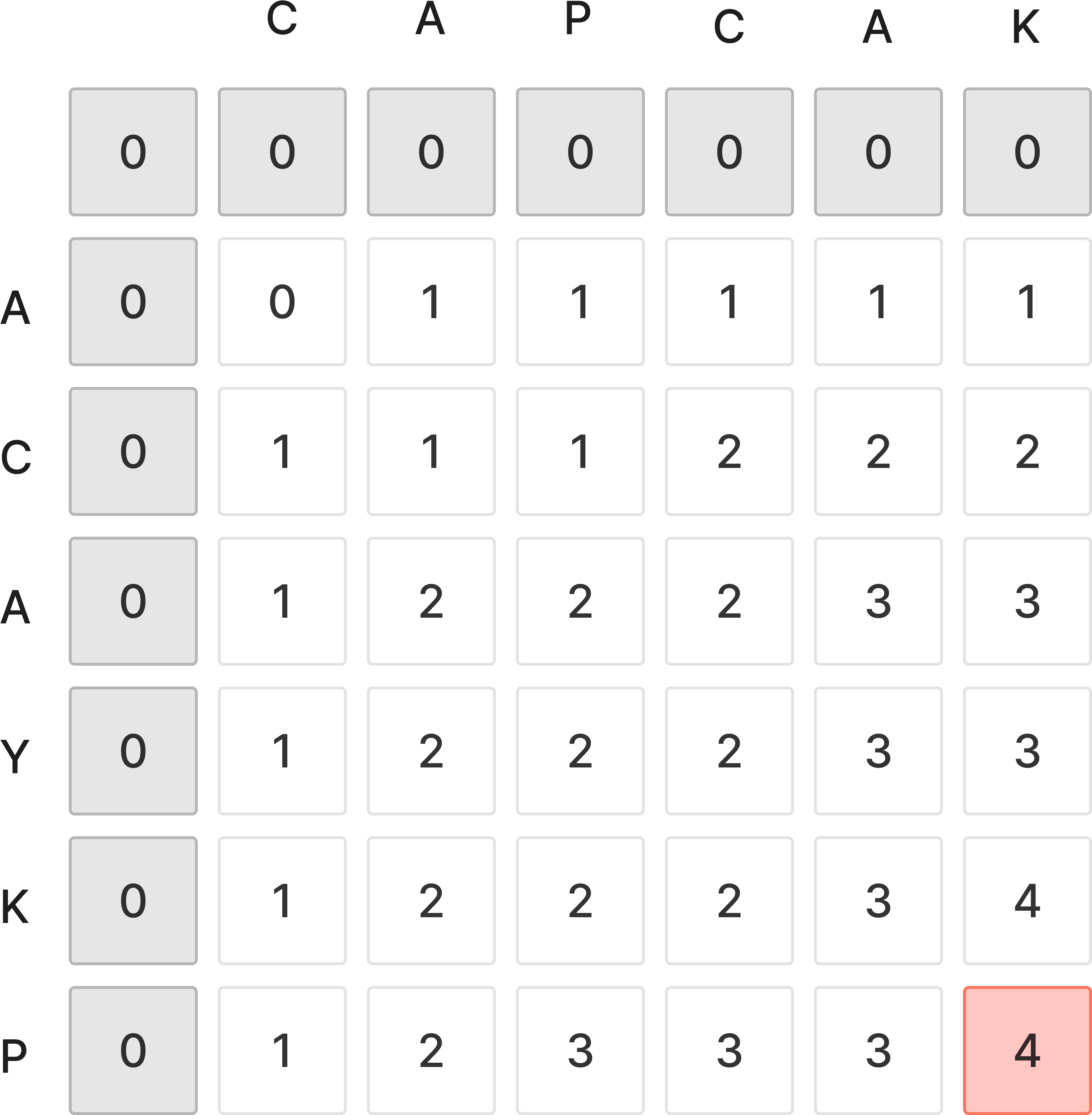
빨간 부분은 두 문자열을 모두 탐색한 결과인 최장 LCS의 길이가 저장된다.
해당 부분을 시작으로 역추적을 시작해 요소들을 구해낼 수 있다.
방법은 간단하다.
메모이제이션을 하는 상황을 반대로 생각해 해당 부분이 어디서 왔는지 따라가는 것이다.
해당 부분에 올 수 있는 경우는 크게 보면 두 가지이다.
- 해당 부분의 요소가 같을 경우: dp[i-1][j-1]로부터 1을 증가시켜 도착했다.
- 해당 부분의 요소가 다를 경우: dp[i-1][j] 혹은 dp[i][j-1] 중 큰 값을 따라왔다.
즉, dp[i-1][j]와 dp[i][j-1] 을 살펴봐 같은 수가 있다면 해당 부분에서 온 것이다.
만약, 그렇지 않다면 dp[i-1][j-1]에서 온 경우이다.
이를 바탕으로 생각해 보면 다음과 같이 정리할 수 있다.
- 위나 왼쪽에 같은 값이 있는 경우: 해당 부분의 요소가 같지 않아 이전의 LCS를 따왔다.
- 위나 왼쪽에 같은 값이 없는 경우: 해당 부분의 요소가 같아 이전 LCS에 자신을 추가했다.
즉, 위나 왼쪽에 같은 값이 있다면 해당 부분을 따라가고 그렇지 않다면 그 요소가 LCS에 포함이 된다는 뜻이 된다.
이를 식으로 정리하면 다음과 같다.
if (dp[N][M] == dp[N - 1][M]) N--;
if (dp[N][M] == dp[N][M - 1]) M--;
lcs.push_back(str1[N]);
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
string str1, str2;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> str1 >> str2;
vector<vector<int>> dp(str1.size() + 1, vector<int>(str2.size() + 1, 0));
for (int i = 1; i <= str1.size(); i++)
{
for (int j = 1; j <= str2.size(); j++)
{
if (str1[i-1] == str2[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
int N = str1.size();
int M = str2.size();
cout << dp[N][M] << "\n";
vector<char> lcs;
while (dp[N][M] != 0)
{
if (dp[N][M] == dp[N - 1][M])
{
N--;
continue;
}
if (dp[N][M] == dp[N][M - 1])
{
M--;
continue;
}
lcs.push_back(str1[N-1]);
N--;
M--;
}
for (int i = lcs.size() - 1; i >= 0; i--)
{
cout << lcs[i];
}
return 0;
}
문제 설명
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
제한 사항


풀이
문제를 요약하면 LCS를 구하는 것이다.
LCS는 최장 공통 부분 수열을 의미한다.
최장 공통 부분 수열은 두 개의 문자열 혹은 배열에서 가장 긴 공통된 부분을 의미한다.
예를 들어 보자.
ACAYKP, CAPCAK 두 개의 문자열의 LCS는 ACAK이다.

그렇다면, 이를 어떻게 구해내는지 알아보자.
LCS는 DP를 이용하여 간단하게 구해낼 수 있다.
이차원 배열을 통해 메모이제이션을 한다.
두 문자열의 각 위치를 비교하며 같을 때와 다를 때를 구분하여 처리한다.
만약, 두 요소가 같다면 이전 문자열에서 해당 요소를 추가한 것이 LCS가 될 것이다.

빨간 부분을 보면, A로 두 문자열이 공통 요소를 갖는다.
이는 이전 단계에서 구한 LCS에 A를 추가하여 얻는 것과 같은 결과이다.
물론 제일 처음 문자이기에 이전 단계가 없다.
회색으로 칠해진 부분은 계산을 용이하게 하기 위한 패딩이다.
하나의 상황을 더 보자.

빨간 부분은 C가 두 문자열의 공통부분이 되는 상황이다.
C를 비교하는 상황의 문자열은 AC와 CAPC가 된다.
이 둘의 LCS는 AC이다.
즉, C이전에 찾은 LCS인 A에 C를 추가하여 만드는 상황이다.
따라서, dp[i-1][j-1]에 1을 추가한 것과 같다.
if(str1[i] == str2[j]) dp[i][j] = dp[i-1][j-1];
그럼 두 요소가 다른 경우는 어떤지 살펴보자.
두 요소가 다르다면 LCS는 이전에 만들어 놓은 LCS중 하나가 될 것이다.
이때, 두 가지 선택지가 있다.
str1에서 1개가 빠진 것이 최장 LCS일지 str2에서 1개가 빠진 것이 최장 LCS일지 모른다.
예를 들어 보자.

빨간 부분을 보면 ACA와 CAP를 비교하는 과정이다.
이때 A와 P는 다르기 때문에 이전에 찾아 놓은 LCS를 기록하려 한다.
[AC - CAP], [ACA - CA] 둘 중 더 긴 LCS를 골라야 한다.
- AC-CAP: A
- ACA-CA: CA
후자의 경우가 더 긴 LCS를 갖고 있다.
이를 식으로 정리해 보면 다음과 같다.
if(str1[i] != str2[j]) dp[i][j] = max(dp[i-1][j], dp[i][j-1]);이렇게 모든 문자열을 탐색하면 최장 LCS의 길이를 구해낼 수 있다.
그렇다면, 최장 LCS가 갖는 요소들을 찾아내야 한다.
이 역시 간단한 방법으로 구할 수 있다.
메모이제이션을 모두 완료하면 다음과 같은 상황이다.

빨간 부분은 두 문자열을 모두 탐색한 결과인 최장 LCS의 길이가 저장된다.
해당 부분을 시작으로 역추적을 시작해 요소들을 구해낼 수 있다.
방법은 간단하다.
메모이제이션을 하는 상황을 반대로 생각해 해당 부분이 어디서 왔는지 따라가는 것이다.
해당 부분에 올 수 있는 경우는 크게 보면 두 가지이다.
- 해당 부분의 요소가 같을 경우: dp[i-1][j-1]로부터 1을 증가시켜 도착했다.
- 해당 부분의 요소가 다를 경우: dp[i-1][j] 혹은 dp[i][j-1] 중 큰 값을 따라왔다.
즉, dp[i-1][j]와 dp[i][j-1] 을 살펴봐 같은 수가 있다면 해당 부분에서 온 것이다.
만약, 그렇지 않다면 dp[i-1][j-1]에서 온 경우이다.
이를 바탕으로 생각해 보면 다음과 같이 정리할 수 있다.
- 위나 왼쪽에 같은 값이 있는 경우: 해당 부분의 요소가 같지 않아 이전의 LCS를 따왔다.
- 위나 왼쪽에 같은 값이 없는 경우: 해당 부분의 요소가 같아 이전 LCS에 자신을 추가했다.
즉, 위나 왼쪽에 같은 값이 있다면 해당 부분을 따라가고 그렇지 않다면 그 요소가 LCS에 포함이 된다는 뜻이 된다.
이를 식으로 정리하면 다음과 같다.
if (dp[N][M] == dp[N - 1][M]) N--;
if (dp[N][M] == dp[N][M - 1]) M--;
lcs.push_back(str1[N]);
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
string str1, str2;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> str1 >> str2;
vector<vector<int>> dp(str1.size() + 1, vector<int>(str2.size() + 1, 0));
for (int i = 1; i <= str1.size(); i++)
{
for (int j = 1; j <= str2.size(); j++)
{
if (str1[i-1] == str2[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
int N = str1.size();
int M = str2.size();
cout << dp[N][M] << "\n";
vector<char> lcs;
while (dp[N][M] != 0)
{
if (dp[N][M] == dp[N - 1][M])
{
N--;
continue;
}
if (dp[N][M] == dp[N][M - 1])
{
M--;
continue;
}
lcs.push_back(str1[N-1]);
N--;
M--;
}
for (int i = lcs.size() - 1; i >= 0; i--)
{
cout << lcs[i];
}
return 0;
}
