문제 설명
세 개의 단어가 주어졌을때, 꿍은 첫 번째 단어와 두 번째 단어를 섞어서 세 번째 단어를 만들 수 있는지 궁금해졌다. 첫 번째와 두 번째 단어는 마음대로 섞어도 되지만 원래의 순서는 섞여서는 안 된다. 다음과 같은 경우를 생각해보자.
- 첫 번째 단어 : cat
- 두 번째 단어 : tree
- 세 번째 단어 : tcraete
보면 알 수 있듯이, 첫 번째 단어와 두 번째 단어를 서로 섞어서 세 번째 단어를 만들 수 있다. 아래와 같이 두 번째 예를 들어보자.
- 첫 번째 단어 : cat
- 두 번째 단어 : tree
- 세 번째 단어 : catrtee
이 경우 역시 가능하다. 그렇다면 "cat"과 "tree"로 "cttaree"를 형성하는건 불가능하다는걸 눈치챘을 것이다.
제한 사항

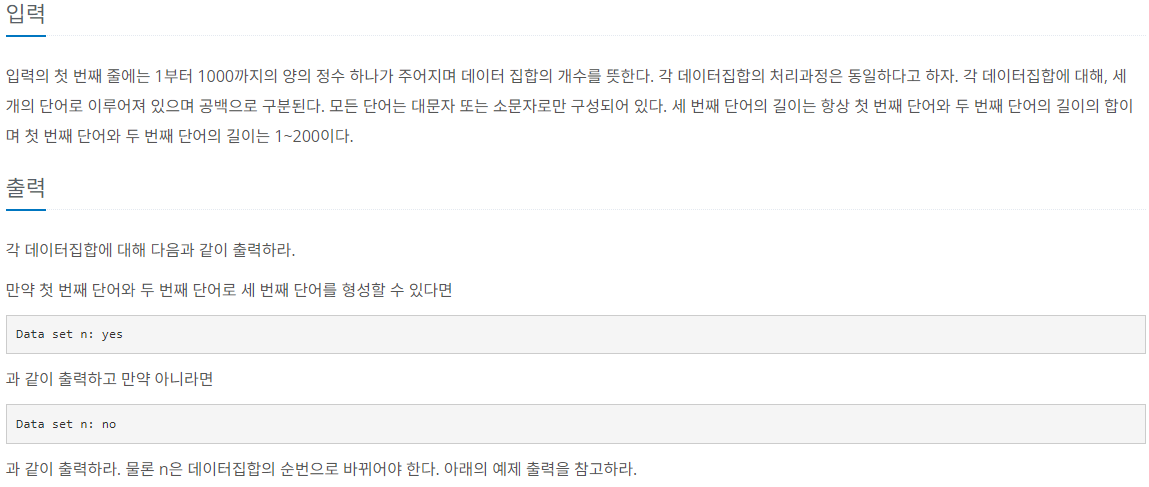
풀이
문제를 요약하면, 두 단어를 섞어 세 번째 단어를 만드는 것이다.
이때, 각 단어의 순서는 섞여서는 안 된다.
처음 문제를 봤을 때, BFS를 통해 단어의 앞에서부터 하나씩 넣으며 만들 수 있는지 확인하면 된다고 생각했다.
하지만, 해당 방법은 메모리 초과가 발생했다.
메모리를 줄이기 위해서는 분기를 처리하거나 메모이제이션을 통한 DP를 사용해야 된다.
하지만, 완성된 단어로 방문여부를 체크하는 것은 사용한 단어의 철자에 따라 달라지기 때문에 불가능하고 인덱스로 체크를 한다고 하면 DP를 사용하는 것이 좋다고 생각했다.
DP는 다음과 같이 진행된다.
A의 i-1, B의 j-1까지 사용해서 C의 i+j-1까지 만들 수 있는지 확인하면 된다.
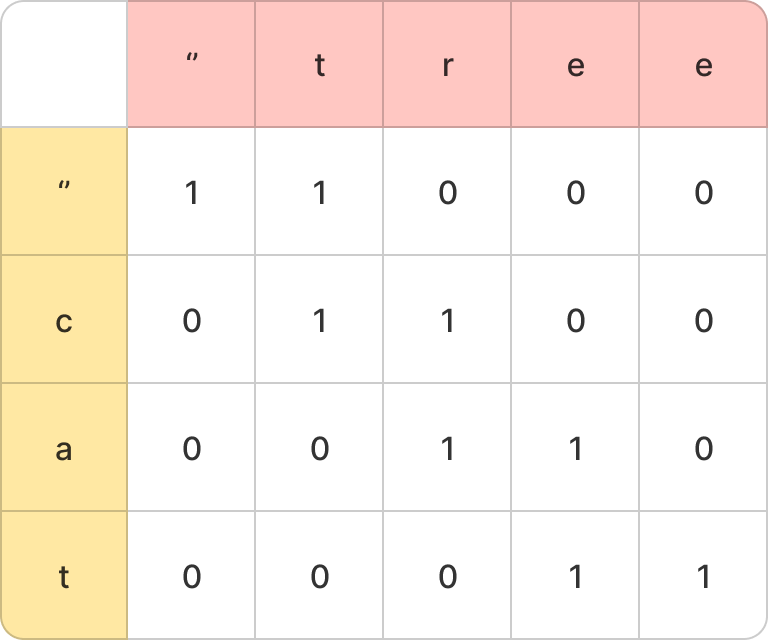
예를 들어, c(i=1)와 t(j=1)까지만 사용하여 tcraete의 t(i+j-1)를 만들 수 있는지를 확인하여 표를 채우면 된다.
그렇다면, 표를 채우는 방법은 다음과 같다.
A를 사용한다 가정하면 C의 i+j-1번째와 A의 i-1번이 같은지 확인해야 하며, i-1을 사용하기 이전의 문자를 만들 수 있는지 동시에 확인해야 한다.
if(dp[i - 1][j] && a[i - 1] == c[i + j - 1])B를 사용한다 가정하면 C의 i+j-1번째와 B의 j-1번이 같은지 확인해야 하며, j-1번을 사용하기 이전의 문자를 만들 수 있는지 확인해야 한다.
if(dp[i][j - 1] && b[j - 1] == c[i + j - 1])
표를 모두 채운 후, 마지막칸이 1인지 아닌지를 확인하면 된다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
bool GetPossible(string a, string b, string c)
{
vector<vector<int>> dp(a.size()+1, vector<int>(b.size()+1, 0));
dp[0][0] = 1;
int alen = a.size();
int blen = b.size();
//행채우기
for (int i = 1; i <= alen; i++)
{
if (a[i - 1] == c[i - 1] && dp[i - 1][0]) dp[i][0] = 1;
}
for (int i = 1; i <= blen; i++)
{
if (b[i - 1] == c[i - 1] && dp[0][i - 1]) dp[0][i] = 1;
}
for (int i = 1; i <= alen; i++)
{
for (int j = 1; j <= blen; j++)
{
if ((dp[i - 1][j] && a[i - 1] == c[i + j - 1]) || (dp[i][j - 1] && b[j - 1] == c[i + j - 1]))
{
dp[i][j] = 1;
}
}
}
return dp[alen][blen];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
for (int t = 1; t <= N; t++)
{
string a, b, c;
cin >> a >> b >> c;
if (GetPossible(a, b, c)) cout << "Data set " << t << ": yes\n";
else cout << "Data set " << t << ": no\n";
}
return 0;
}
문제 설명
세 개의 단어가 주어졌을때, 꿍은 첫 번째 단어와 두 번째 단어를 섞어서 세 번째 단어를 만들 수 있는지 궁금해졌다. 첫 번째와 두 번째 단어는 마음대로 섞어도 되지만 원래의 순서는 섞여서는 안 된다. 다음과 같은 경우를 생각해보자.
- 첫 번째 단어 : cat
- 두 번째 단어 : tree
- 세 번째 단어 : tcraete
보면 알 수 있듯이, 첫 번째 단어와 두 번째 단어를 서로 섞어서 세 번째 단어를 만들 수 있다. 아래와 같이 두 번째 예를 들어보자.
- 첫 번째 단어 : cat
- 두 번째 단어 : tree
- 세 번째 단어 : catrtee
이 경우 역시 가능하다. 그렇다면 "cat"과 "tree"로 "cttaree"를 형성하는건 불가능하다는걸 눈치챘을 것이다.
제한 사항


풀이
문제를 요약하면, 두 단어를 섞어 세 번째 단어를 만드는 것이다.
이때, 각 단어의 순서는 섞여서는 안 된다.
처음 문제를 봤을 때, BFS를 통해 단어의 앞에서부터 하나씩 넣으며 만들 수 있는지 확인하면 된다고 생각했다.
하지만, 해당 방법은 메모리 초과가 발생했다.
메모리를 줄이기 위해서는 분기를 처리하거나 메모이제이션을 통한 DP를 사용해야 된다.
하지만, 완성된 단어로 방문여부를 체크하는 것은 사용한 단어의 철자에 따라 달라지기 때문에 불가능하고 인덱스로 체크를 한다고 하면 DP를 사용하는 것이 좋다고 생각했다.
DP는 다음과 같이 진행된다.
A의 i-1, B의 j-1까지 사용해서 C의 i+j-1까지 만들 수 있는지 확인하면 된다.

예를 들어, c(i=1)와 t(j=1)까지만 사용하여 tcraete의 t(i+j-1)를 만들 수 있는지를 확인하여 표를 채우면 된다.
그렇다면, 표를 채우는 방법은 다음과 같다.
A를 사용한다 가정하면 C의 i+j-1번째와 A의 i-1번이 같은지 확인해야 하며, i-1을 사용하기 이전의 문자를 만들 수 있는지 동시에 확인해야 한다.
if(dp[i - 1][j] && a[i - 1] == c[i + j - 1])B를 사용한다 가정하면 C의 i+j-1번째와 B의 j-1번이 같은지 확인해야 하며, j-1번을 사용하기 이전의 문자를 만들 수 있는지 확인해야 한다.
if(dp[i][j - 1] && b[j - 1] == c[i + j - 1])
표를 모두 채운 후, 마지막칸이 1인지 아닌지를 확인하면 된다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
bool GetPossible(string a, string b, string c)
{
vector<vector<int>> dp(a.size()+1, vector<int>(b.size()+1, 0));
dp[0][0] = 1;
int alen = a.size();
int blen = b.size();
//행채우기
for (int i = 1; i <= alen; i++)
{
if (a[i - 1] == c[i - 1] && dp[i - 1][0]) dp[i][0] = 1;
}
for (int i = 1; i <= blen; i++)
{
if (b[i - 1] == c[i - 1] && dp[0][i - 1]) dp[0][i] = 1;
}
for (int i = 1; i <= alen; i++)
{
for (int j = 1; j <= blen; j++)
{
if ((dp[i - 1][j] && a[i - 1] == c[i + j - 1]) || (dp[i][j - 1] && b[j - 1] == c[i + j - 1]))
{
dp[i][j] = 1;
}
}
}
return dp[alen][blen];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
for (int t = 1; t <= N; t++)
{
string a, b, c;
cin >> a >> b >> c;
if (GetPossible(a, b, c)) cout << "Data set " << t << ": yes\n";
else cout << "Data set " << t << ": no\n";
}
return 0;
}